Qu'est-ce qu'une fibre optique?
Modes de propagation de la lumière dans une fibre optique
Modèle des rayons
On va d'abord traiter la propagation de la lumière à l'intérieur de la fibre avec un modèle simple géométrique appelé modèle des rayons. le type de la fibre est définie en fonction du profil de distribution de l'indice de réfraction avec lequel la fibre est fabriquée.
On va considérer une fibre optique à saut d'indice et à symétrie circulaire dont le coeur est de rayon a et d'indice de réfraction n1, la gaine est de rayon r et d'indice de réfraction n2. C'est une fibre à saut d'indice car c'est le type de fibres généralement utilisées.
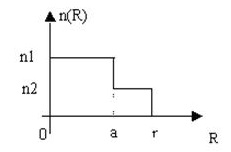
Les rayons lumineux entrant dans la fibre suivent différents chemins pendant qu'ils se propagent le long de la
fibre, ils subissent de multiples fois des réflexions totales à l'interface coeur-gaine et donc restent guidés dan le coeur.

Le principe de réflextion totale interne ainsi que les conditions pour lesquelles la lumière reste guidée
dans le coeur ont été traitées dans le Rapport du stage.
L'approche géométrique reste schématique il faut considérer un modèle plus subtile et plus
riche qui est celui des Modes de propagation. En faisant les approximations suivantes :
==> Milieu isolant, non magnétique, isotrope, linéaire et homogène,
==> Guidage faible des modes c'est-à-dire ∆n = n1−n2 << n1 nous permet de négliger les effets de la polarisation dans notre étude,
==> Pour des raisons de géométrie liées à la fibre, on considère un système de coordonnées cylindriques (r, ϕ, z), on simplifie les équations
de Maxwell ainsi que l'équation de propagation qui en découle. On détermine donc les Modes de propagation qui sont
les solutions approximatives valables dans ces conditions qui s'écrivent au moyen des fonctions de Bessel:

Chaque famille de modes est décrite par un nombre entier l (0,1,2,3....) et le nombre entier m (1,2,3...)
correspond au numéro de la solution, donc pour chaque valeur donnée de l on aura plusieurs modes guidés
désignés par Modes LPlm On peut donc définir deux sortes de fibres en fonction du nombre de
modes qui peuvent se propager à l'intérieur.
==> Single Mode Fiber (SMF)
==> Multi-Mode Fiber (MMF)
A cause de la géométrie circulaire de la fibre, seuls les Modes LP0m seront
excités, d'où notre interêt pour ce type de modes.