Modélisation de systèmes d'optique astronomique 

Projet tuteuré réalisé au laboratoire Lagrange sous la tutelle de Marcel Carbillet

Introduction générale

          Les astronomes sont confrontés, lors de leurs observations, à plusieurs problèmes. Entre autres, à la perte de résolution angulaire dans l'image formée au foyer du téléscope, due à la turbulence optique se développant au sein de l'atmosphère terrestre traversée. 


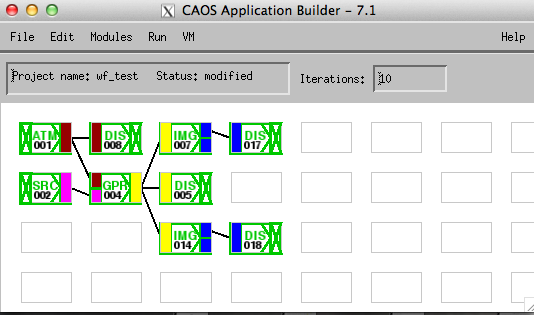
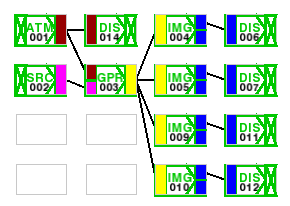
          Nous avons modélisé ce phénomène physique par le biais de l'outil de simulation de systèmes d'optique astronomique CAOS ( Code for Adaptive Optics Systems). 

          Cet outil, utilisé par les chercheurs, est en perpétuelle évolution grâce aux modifications qu'ils peuvent apporter. Cela peut aller de l'amélioration de son ergonomie à l'ajout de nouvelles fonctionnalités. 
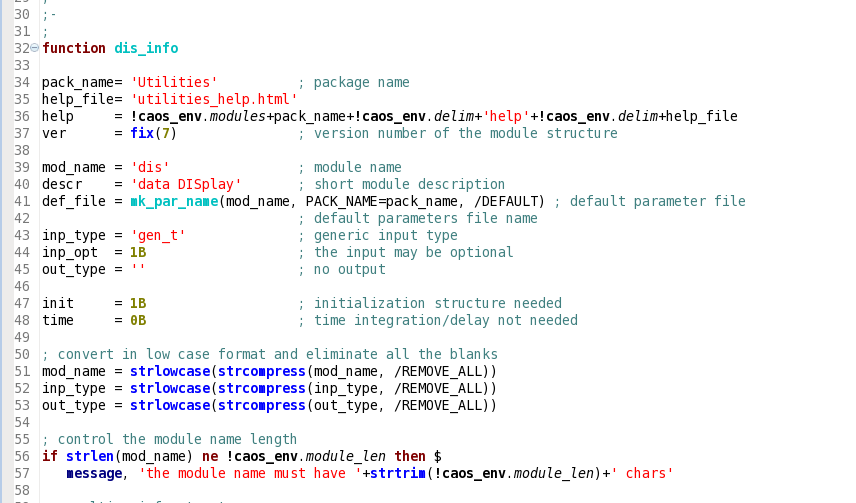
Une partie de notre projet a été de contribuer à ces modifications.

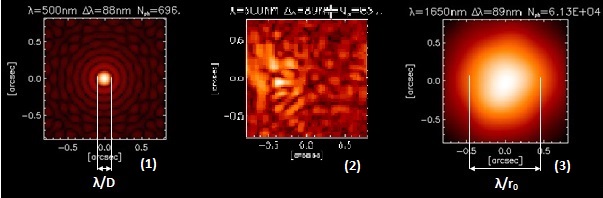
          Par la suite, nous avons exploité l'application pour simuler des images déformées par la présence d'une atmosphère turbulente ou non, en fonction de plusieurs paramètres décrivant le système.  
Cela nous a permi de comparer ces mesures avec plusieurs théories connues : celle de notre cours d'Optique Ondulatoire et de l'astronome Roddier.

          Cette vidéo montre l'éxecution d'un projet sous PSE CAOS permettant de simuler une image déformée par une atmosphère turbulente. 




L'interface graphique utilisateur

          Cette interface se présente à l'ouverture de l'Application Builder (lisez "Constructeur d'Application"). 

           L'utilité finale de cette interface est de construire un système de simulation incluant une source dont on définit le type dans le module SRC, une atmosphère (module ATM) dont on choisi d'établir la turbulence ou non, et un système d'imagerie nous redonnant une réponse impulsionnelle déformée de l'astre observé. 
La strucure modulaire est détaillée plus bas.

          Par exemple, la simulation montrée dans la vidéo est issue de ce projet, affiché dans l'Application builder de CAOS PSE, permettant d'agencer à souhait les modules :


Exemple de projet de simulation affichant la réponse impulsionnelle
d'un front d'onde ayant traversé une atmosphère.    

          

          Ce projet sert à simuler les figures de speckle observées au foyer du télescope d'un mètre de diamètre C2PU du plateau de Calern. Les modules suivants ont permi cette simulation :

  • SRC → source lumineuse stellaire ;
  • ATM → atmosphère turbulente ;
  • GPR → propagation géométrique de la source lumineuse à travers l'atmosphère ;
  • IMG → formation de la réponse impulsionnelle de l'astre au foyer du téléscope ;
  • DIS → affichage de l'image (puissance, log, zoom, dimensions ...) ;

          Dans le cadre de notre projet, nous nous servons du Software Package  CAOS : la trentaine de modules qu'il contient servent à modéliser des systèmes d'un domaine scientifique bien précis, celui de l'Optique Adaptative.


Les modules

          Ceux-ci se présentent à nous sur l'interface graphique, comme des rectangles où sont indiqués les noms de modules reliés logiquement entre eux.

          Un module (un rectangle) a une fonction bien precise, établie par un groupe de fichiers de code source sous langage IDL. 

          Par exemple, pour le module DIS (data DISplay) d'affichage des données, le groupe de fichier est composé des  fichiers suivants (un fichier égal à une routine) :




        
  • dis_gen_default.pro : génère une strucure de paramètres par défaut pour le module DIS, du                      package CAOS 7.0 et l'enregistre dans le répertoire approprié ;                                               
  • dis_prog.pro : représente l'algorithme scientifique du module DIS ;
  • dis_init.pro : routine d'éxécution d'une initialisation pour le module DIS en vue de plusieurs                      itérations du traitement ;
  • dis_info.pro : renvoie les informations de base pour DIS ;
  • dis_gui.pro : génère la Graphical User Interface (GUI) ou interface graphique utilisateur ;
  • dis.pro : éxécute la simulation du module DIS. 
    Ce module propose l'affichage d'un champ approprié pour chaque type de sortie du package (des exemples de type de sorties sont détaillés plus bas).

Voici un exemple de réponses impulsionnelles extraites de simulations réalisées avec CAOS :


Réponses impulsionnelles dépendant chacunes  de paramètres différents du système d'observation.

          L'image (1) est la fonction de répartition du point d'un astre supposé à l'infini, sans atmosphère turbulente. 
Etant donné que l'objectif du télescope est simplifié par un masque circulaire de diamètre D, la fonction d'étalement du point est une tache d'Airy, où sa tache centrale est de largeur   λ/ D.

 

          L'image (2) représente la réponse impulsionnelle d'un astre qui cette fois a été soumise à une atmosphère turbulente : ceci provoque l'apparition de speckle, ou tavelures.
En effet, l'onde incidente, de la forme Ψ(r) = A(r) exp(iφ(r)), où φ est sa phase subit, lors de la traversée de l'atmopshère turbulente, plusieurs sortes de perturbations. Chacune est impliquée dans l'apparition des speckle :

  • la scintillation → variation dans le temps de l'amplitude A(r) reçue par la pupille ;
  • l'agitation → variation de la pente moyenne de la phase de l'onde ;
  • l'étalement → perte de cohérence spatiale de la phase.


          Ces perturbations interviennent sur la phase de l'onde seulement durant les dizaines de derniers kilomètres restants à parcourir à la lumière provenant de l'astre observé. 

          Ce phénomène de perte de résolution angulaire dans l'image formée au foyer du téléscope sont dues à l'atmosphère turbulente qui a une taille caractéristique, qui est l'échelle externe de la turbulence optique. Cette dernière est constituée de tourbillons "emboîtés" les uns dans les autres :


          La figure (3) montrant la réponse impulsionnelle en long temps de pose (t pose>>τ 0, défini plus bas) nous permet d'introduire le paramètre de Fried r 0. C'est la taille caractéristique des zones de cohérence spatiale qui se trouvent sur la pupille. 

          La définition de ce paramètre nous permet d'expliquer pourquoi les perturbations de la phase dépendent de la longueur d'onde λ :

r 0= 0.185 λ 6/ 5 [∫C 2 N(z) dz] -3/ 5


Si ce r 0est plus petit que le diamètre du téléscope D, on peut observer des speckles, comme sur la seconde image.  Ainsi, r 0est le diamètre d'un télescope sans présence d'atmosphère turbulente.
                 
Etant donné qu'il est la plupart du temps plus petit que le diamètre du télescope D, cela explique la raison pour laquelle la largeur à mi-hauteur λ/ r 0 de la tache long temps de pose avec une atmosphère turbulente est plus grande que celle sans atmosphère turbulente, λ/ D.

Nous introduisons deux valeurs qui caractérisent entre autres le système d'observation étudié, dépenantes du paramètre de Fried r 0:

τ 0= 0.36 r 0 / v

représente le temps d'évolution typique de la turbulence, avec v la vitesse de déplacement des couches turbulentes, pondéré par C 2 N(h), le profil de turbulence.

θ 0= 0.36 r 0 / h

est l'angle formé par deux visées sous lequel on peut considérer un même perturbation, où h est la hauteur pondérée des couches turbulentes.


© 2016 Adama Sy & Perruchon-Monge Ulysse