Modélisation de systèmes d'optique astronomique 

Projet tuteuré réalisé au laboratoire Lagrange sous la tutelle de Marcel Carbillet

Mesures effectuées

          Nous allons mesurer ici la largeur a mi-hauteur des images obtenues en fonction de plusieurs paramètres du système. Ceci sert à caractériser l'effet de ces paramètres sur la réponse impulsionnelle : L 0, la présence d'une atmopshère turbulente, la longueur d'onde de l'onde incidente ...

          En imagerie astronomique, la largeur à mi-hauteur d'une réponse impulsionnelle est appelée seeing.
Il désigne la qualité d'image et mesure la perturbation atmosphérique que traverse la lumière de l'étoile.
Notre simulation d'une image d'un astre aura pour but de déterminer la largeur à mi-hauteur de la fonction d'étalement de cet astre, dans un cas sans atmosphère turbulente, dans un autre cas avec la présence de celle-ci, en faisant varier L 0. 

          Nous savons que, comme expliqué dans l' introduction générale, la réponse impulsionnelle obtenue lors de l'observation d'un astre dépend de la longueur d'onde. 
Nous réalisons la simulation pour deux longueurs d'onde différentes : 500 nm (bande V, visible) et 1650 nm (bande H, Infrarouge). 
De manière directe, la largeur à mi-hauteur donne accès à la valeur de la résolution.

          Etant donné que les réponses impulsionnelles sont assimilables à une gaussienne, nous pourrons comparer la largeur à mi-hauteur des réponses impulsionnelles à une gaussienne qui épousera au mieux cette dernière. Ceci est rendu possible grâce à une fonction propre à IDL : gauss2dfit.

 

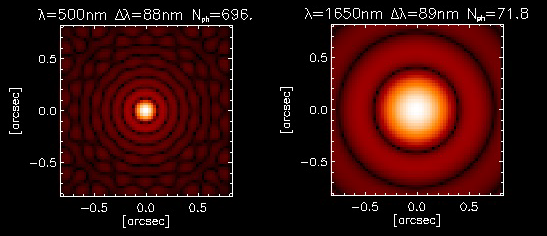
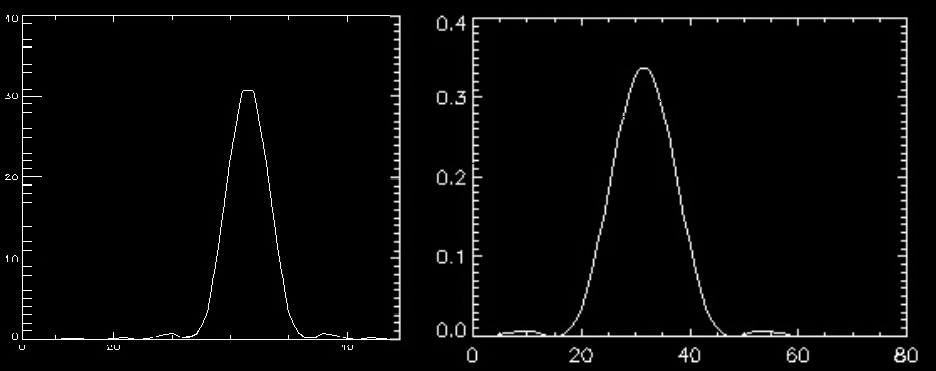
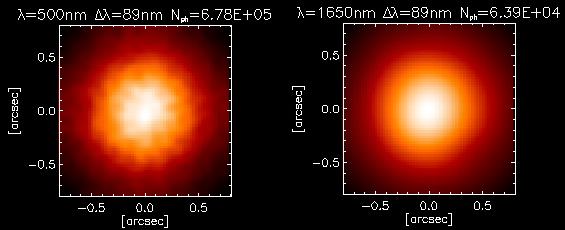
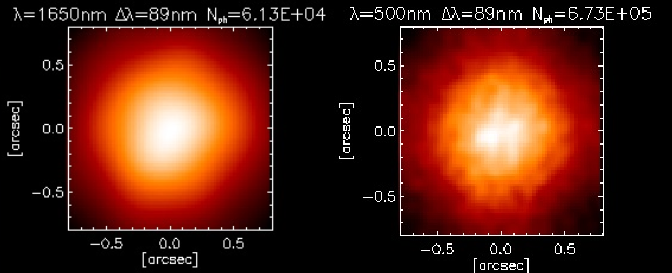
Ajustement de la réponse impulsionnelle

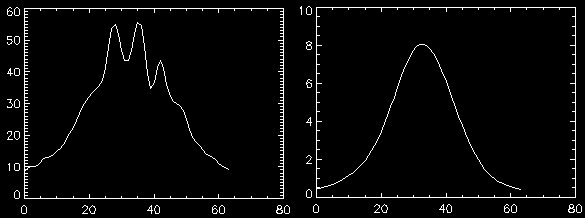
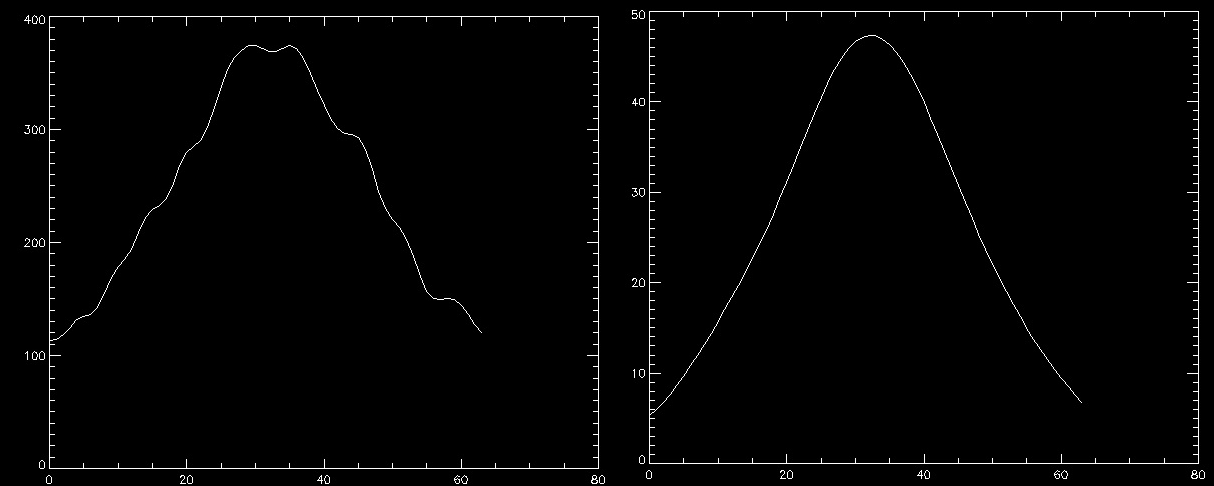
          Nous allons ajuster une gaussienne à notre fonction d'étalement du point afin d'accéder aux écarts-types qui nous permettront de calculer sa largeur à mi-hauteur.

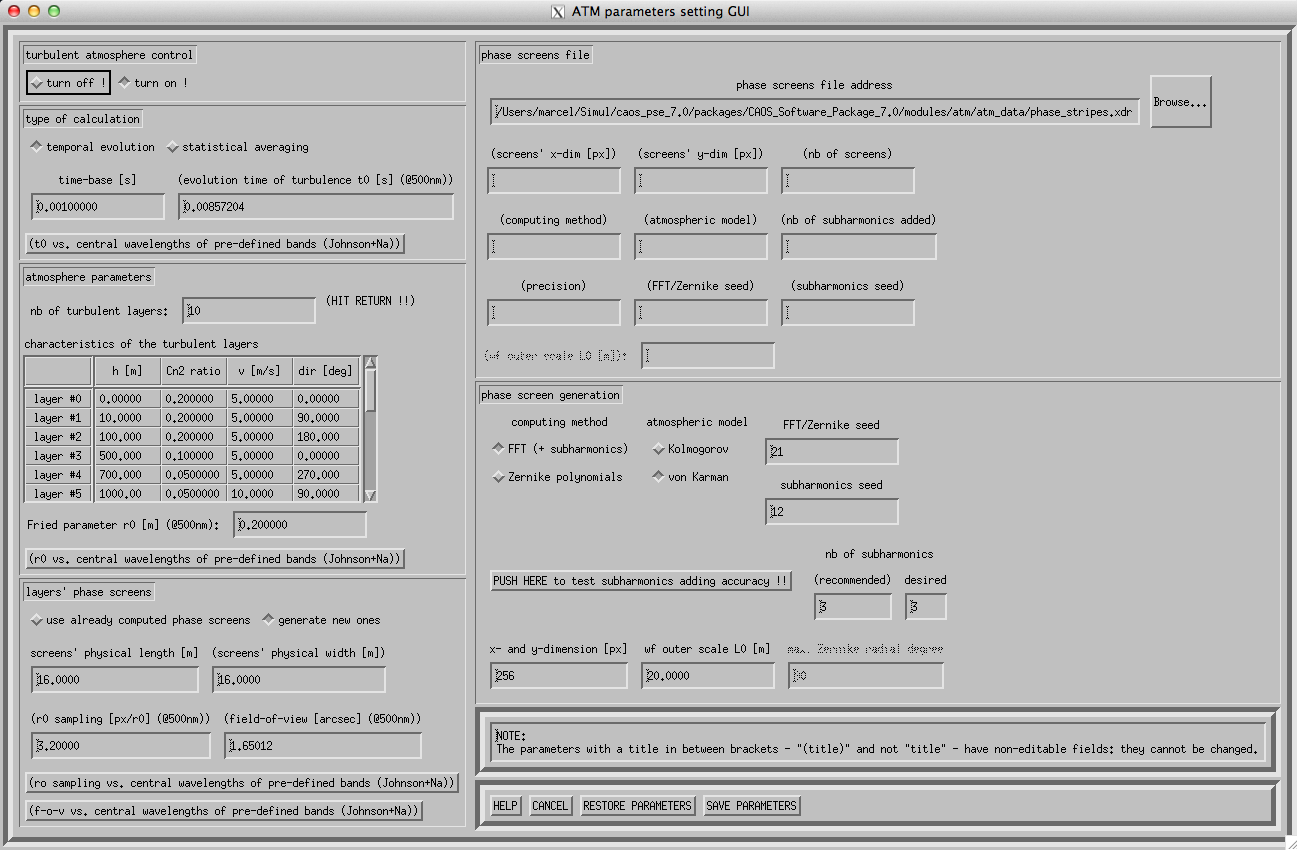
          Le projet de simulation créé sur le worksheet, nous choisissons de l'éxecuter depuis le terminal : la fonction ".r"+"chemin d'accès au fichier du projet en .pro" permet ceci.
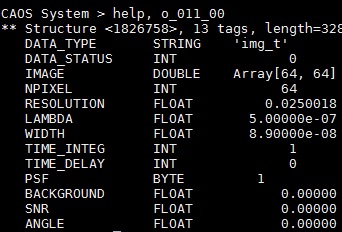
Cette éxecution depuis le terminal nous donne accès à toutes les informations numériques liées à un module en particulier, à l'issu de la simulation, grâce à la commande "help, référence du module". La référence du module est sous la forme o_"#module"_"#sortie". Ici, o_011_00.

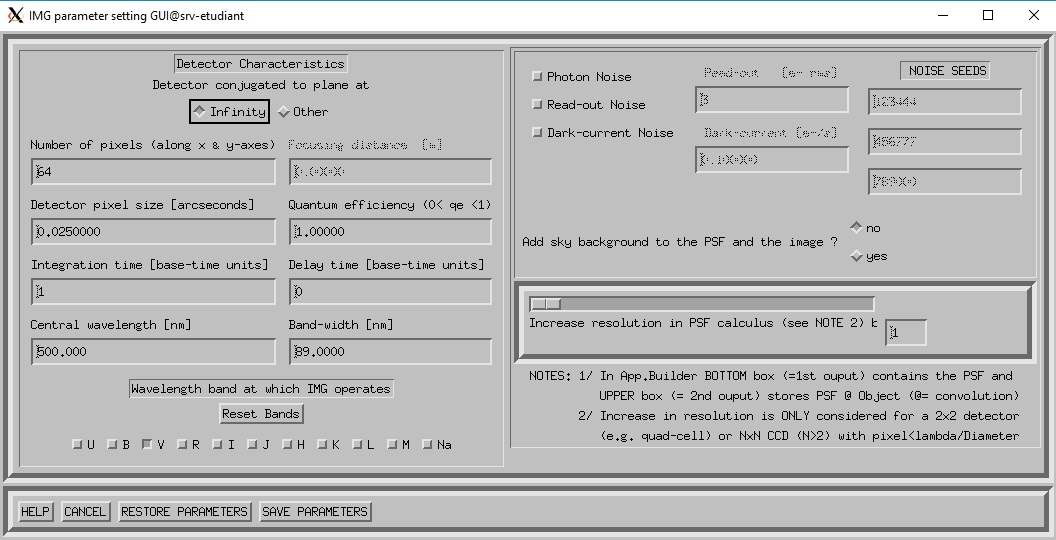
          C'est le module IMG qui nous intéresse car il contient la réponse impulsionnelle sous forme de tableau 64x64 que nous souhaitons analyser. 





Mon Image

          Toutes les caractéristiques du module sont présentes : type de données, image (tableau 64x64), sa résolution (0.025 px), et les autres valeurs renseignées lors du réglage du module. 

          On s'intéresse ici à 0_011_00.image (sélectionne le tableau représentant l'image), que l'on nomme img.
La gaussienne est donnée par une routine d'IDL : gauss2dfit(img,a), où a est une variable sur laquelle les coefficients de l'ajustement son retournés : localisation du centre, sa largeur, son facteur d'échelle... et représentés par a("# argument"). a(2) et a(3) sont les écarts-types de la gaussienne dans la direction X et Y respectivement.
Connaissant la forme d'une gaussienne, on peut en déduire :

e -( FWHM⁄ 2) 2/2σ 2 = 1/2 ⇔ FWHM = 2σ√[2ln(2)]

Le calcul de la FWHM se ramène donc à connaître σ = (a(2)+a(3))/2.               

Calcul des largeurs à mi-hauteur

Nous allons calculer les FWHM pour des paramètres de modules différents, à savoir :

  • la longueur d'onde λ : 500 nm et 1650 nm (bandes V et H);
  • la présence d'une atmosphère turbulente ou non. Si oui, nous avons fait varier l'échelle externe L 0afin de confirmer la théorie de Roddier, évoquée dans la partie correspondante.

Sans atmosphère turbulente

Ci-après, les images des GUI des modules paramétrés pour la simulation :

Paramètres des modules dans le cas d'une atmosphère non turbulente.
Modules Paramètres
ATM Sans atmosphère turbulente
SRC Source ponctuelle à l'infini

GPR

∅ du téléscope : 1m, sans obstruction centrale
IMG λ = 500 nm/1650 nm, Δx = 0.025 arcsec, # de pixels : 64×64, sans bruit
DIS table de couleur rouge, image élevée à la puisance 0.2

          Après avoir défini les paramètres propres à chaque module, nous l'enregistrons dans le dossier par défaut ~/Projects/nomduprojet/project.pro . Notre projet porte le nom de "test".
Nous nous servons de la commande >.r Projects/test/project.pro.
Le programme s'éxecute comme montré sur la vidéo de simulation d'un projet. 

Nous nous retrouvons avec les deux réponses impulsionnelles suivantes : 

Réponses impulsionnelles pour λ = 500 nm (à gauche) et λ = 1650 nm (à droite).

          Une autre routine d'IDL nous permet d'afficher la coupe de nos réponses impulsionnelles à l'endroit voulu : >plot, img[32,*] ; où [32,*] désigne les coordonnées graphiques. 
Vu que nous voulons sélectionner par exemple toutes les ordonnées pour le centre de la tâche centrale, nous choisissons la 32 ème ligne (le centre des abscisses de l'image) et * qui désigne toutes les ordonnées. 



Coupes des réponses impulsionnelles pour λ = 500 nm et λ = 1650 nm.


          Nous pouvons remarquer qu'il s'agit de fonctions J 1cqui décrivent bien une tache d'Airy (cf cours d'Optique Ondulatoire d'Eric Aristidi). 
Nous comparons la largeur à mi-hauteur de cette fonction à celle de notre réponse impulsionnelle et grâce à l'équation donnée plus haut, nous trouvons :

Largeurs à mi-hauteur en fonction de λ
Théorie 0"0"1031 pour λ = 500 nm
0"3403 pour λ = 1650 nm
Expérience 0"1011 pour λ = 500 nm
0"3335 pour λ = 1650 nm


Les valeurs trouvées avec l'expérience sont relativement proches de la théorie. Cette expérience en est une bonne approximation.

Avec atmosphère turbulente

          Dans cette partie, nous faisons varier un autre paramètre : la taille caractéristique de l'atmosphère turbulente  L 0 . Cette variation va nous permettre de voir comment elle affecte la réponse impulsionnelle, ce qui va nous permettre de valider la théorie de Roddier. 

Nous mettons une atmosphère turbulente avec les paramètres des modules suivants :

Paramètres des modules dans le cas d'une atmosphère non turbulente.
Modules
Paramètres
ATM Avec atmosphère turbulente, r 0= 10 cm, moyenne statistique, L 0= 20m/∞
SRC Source ponctuelle à l'infini
GPR ∅ du téléscope : 1m, sans obstruction cerntrale
IMG λ = 500 nm/1650 nm, Δx = 0.025 arcsec, # de pixels : 64×64, sans bruit, intégration : 100 itérations
DIS table de couleur rouge, image élevée à la puisance 0.2

L 0= 20 m

          
          Comme le cas pour l'absence d'atmosphère, nous éxecutons le projet depuis le terminal. 
Nous trouvons comme valeurs pour la largeur à mi-hauteur des réponses impulsionnelles :

Largeurs à mi-hauteur en fonction de λ
Théorie : λ/r 0= 1"01 pour λ = 500 nm
0"79 pour λ = 1650 nm
Expérience : λ/D = 0"79 pour λ = 500 nm
0"65 pour λ = 1650 nm

Réponses impulsionnelles pour λ = 500 nm et λ = 1650 nm.

          Il s'agit ici de la théorie de Roddier, qui trouve ces valeurs en supposant être dans le modèle de Kolmogorov (L 0→ ∞) : c'est la raison pour laquelle les résulatts trouvés ne se rapprochent pas de la théorie de Roddier. 
Les coupes de ces images donnent :

Coupes des réponses impulsionnelles. 

Remarques :

  • Ces deux coupes permettent de bien voir la différence des réponses impulsionnelles en fonction de λ : l'intensité, pour 500 nm, atteint en son centre des valeurs six fois plus grandes que pour 1650 nm. Ceci est dû à l'étalement spatial.
  • Si nous avions intégré la réponse impulsionnelle de l'onde à 500 nm sur un temps plus long, celle-ci aurait été plus lisse à la manière de celle à 1650 nm.

 

L 0→ ∞

          Nous faisons maintenant tendre L 0→ ∞ pour pouvoir voir l'influence de s'assurer L 0sur les mesures et vérifier la théorie de Roddier évoquée précédemment. Nous trouvons les résultats suivants, comparé à ceux de la théorie :

Largeurs à mi-hauteur en fonction de λ
Théorie : λ/r 0= 1"01 pour λ = 500 nm
0"79 pour λ = 1650 nm
Expérience : λ/D = 0"92 pour λ = 500 nm
0"83 pour λ = 1650 nm

          Ces mesures montrent, pour une taille caractéristique de la couche de turbulences tendant vers ∞, que les largeurs à mi-hauteur se rapprochent sensiblement de la théorie de Roddier. 
Nous pouvons supposer que celles-ci ne sont pas égales car tous les paramètres physiques ne sont pas pris en compte, et parce que nous avons pas la même configuration que celle de Roddier lors de ses mesures.



Réponses impulsionnelles et leur coupe pour  L 0→ ∞

          Grâce à ces mesures, nous avons pu expliciter l'effet d'une variation de longueur d'onde du front d'onde ou de la présence d'une atmosphère turbulente : la déformation de la réponse impulsionnelle y est étroitement liée.