Spectre en longueur
Nous voulons étudier le spectre en longueur de notre cavité. Pour cela nous avons besoin de la partie oscillante de la densité d'état car elle contient la contribution de toutes les orbites périodiques qu’on retrouve dans le billard.
En effet une approximation semiclassique de la densité d'états est donnée par la formule de trace de Gutzwiller qui s'écrit comme la somme d'une partie moyenne et d'une partie oscillante.
Avec la
partie oscillante
qui est de la forme :
Elle va
nous permettre de calculer sa fonction d'autocorrélation :
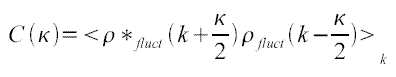
dont la
transformée
de Fourier nous donnera le facteur de forme K(L) qui correspond au
spectre de longueur de notre cavité :
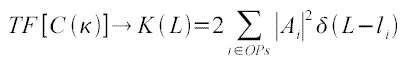
Mais étudier la densité revient à étudier le nombre de modes cumulés à un facteur près(*L²)et dans notre cas, il semble plus approprié de travailler avec le nombre cumulé de modes de la cavité car il s'obtient directement à partir du spectre en fréquence. On à donc :
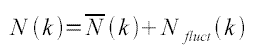
Mais étudier la densité revient à étudier le nombre de modes cumulés à un facteur près(*L²)et dans notre cas, il semble plus approprié de travailler avec le nombre cumulé de modes de la cavité car il s'obtient directement à partir du spectre en fréquence. On à donc :
Avec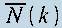 
le
nombre moyen de
mode cumulés à un vecteur d'onde k, qui ne
dépend
que des paramètres géométriques de
l'objet étudié, et qui est
donné par la formule de Weyl pour une cavité
rectangulaire :
le
nombre moyen de
mode cumulés à un vecteur d'onde k, qui ne
dépend
que des paramètres géométriques de
l'objet étudié, et qui est
donné par la formule de Weyl pour une cavité
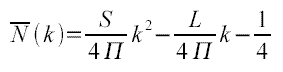
rectangulaire :S
étant la surface
du billard et L son périmètre.
Alors la fonction d'autocorrélation peut se réecrire de la manière suivante :
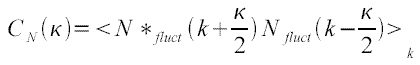
Alors la fonction d'autocorrélation peut se réecrire de la manière suivante :
Et
on obtient le facteur de forme correspondant :
Au final nous aurons donc :
qui représente une série de diracs sur L.
Nous cherchons donc à observer les fluctuations du nombre de modes
cumulés, en fonction de la fréquence, qui va nous
permettre de déterminer le spectre en longueur de
notre cavité.
calcul numérique du spectre en longueur:
Nous avons adapté les étapes qui ont été définies par le calcul théorique précédent à un calcul numérique, sous l'environnement informatique IDL.
En premier lieu nous cherchons à calculer la partie oscillante du nombre de modes cumulés de la cavité qui représente les écarts entre le nombre de modes cumulés N(k) et le nombre moyen de modes cumulés
.En réprésentant numériquement N(k), on peut remarquer qu'il s'agit d'une fonction escalier qui est obtenue par l'étude expérimentale des modes.
Nous allons donc comparer N(k) à la fonction
représentée par la loi de Weyl afin d'en
déterminer les fluctuations.
Ayant obtenu la partie oscillante du nombre de modes cumulés, il reste plus qu'à utiliser la procédure "Fast Fourier Transform" pour voir apparaître le spectre de longueur de la cavité.
Ayant obtenu la partie oscillante du nombre de modes cumulés, il reste plus qu'à utiliser la procédure "Fast Fourier Transform" pour voir apparaître le spectre de longueur de la cavité.
