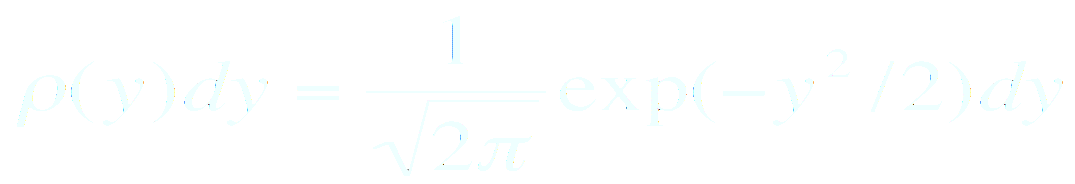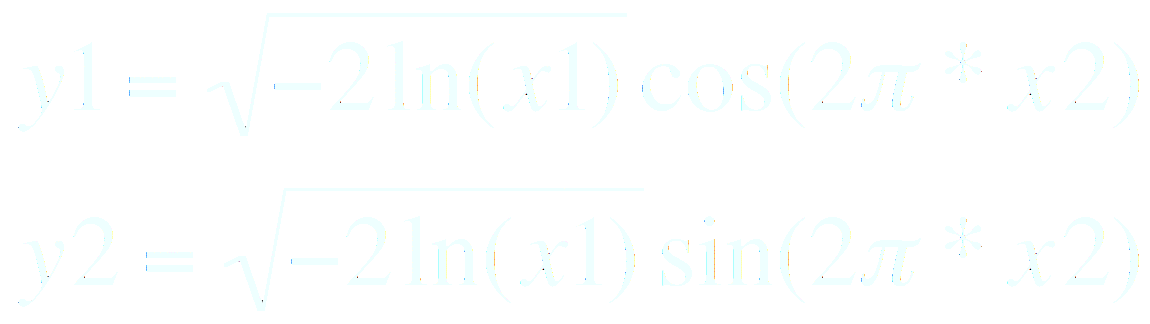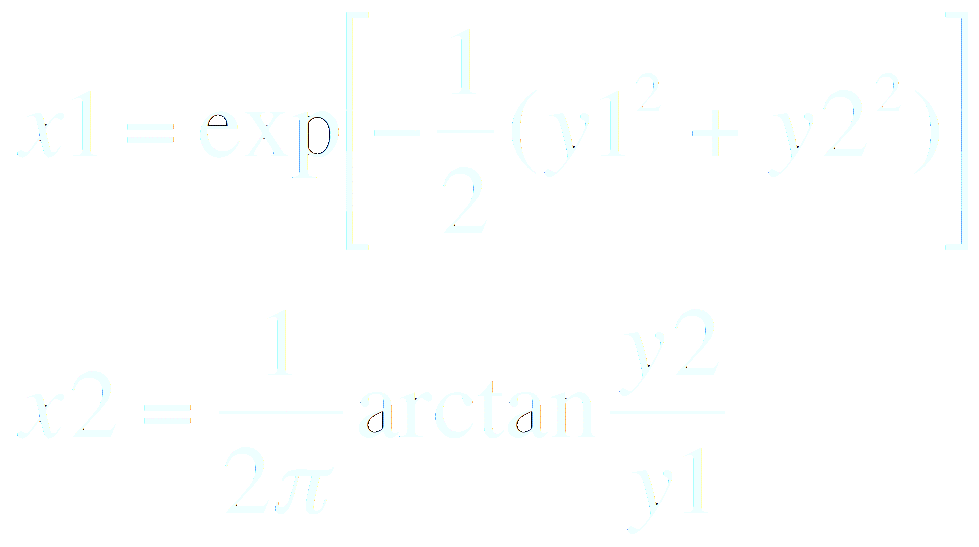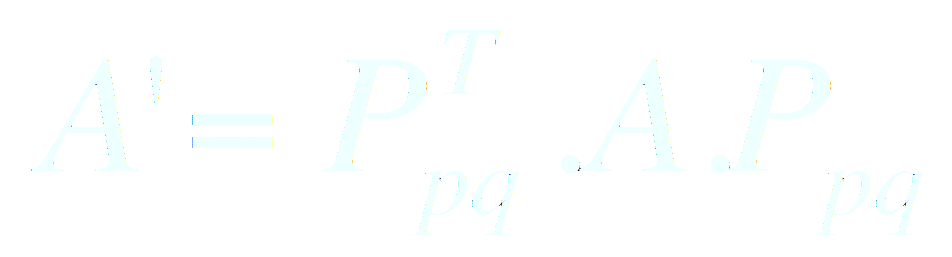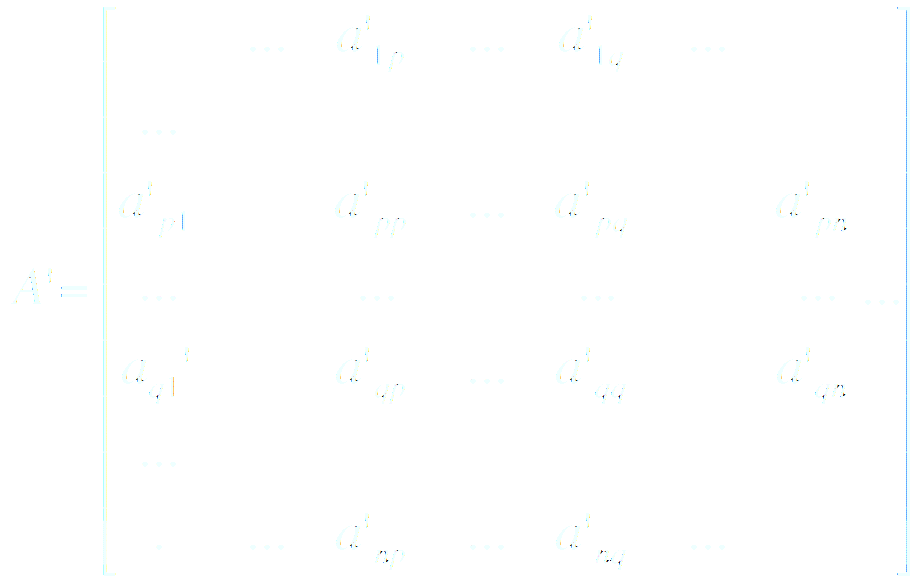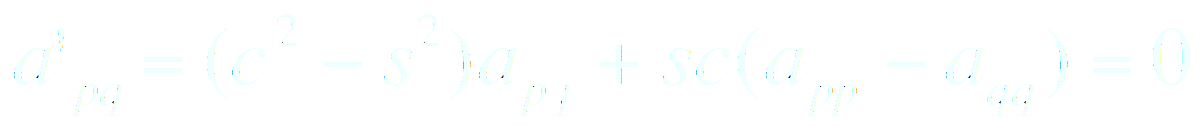Les fonctions Ran :
Les générateurs de nombres aléatoires utilisent un principe d’itération
I(n+1) = a*I(n) (mod m)
où a = 75
m = 231-1 (a et m étant tous deux des nombres premier)
On approxime ensuite une factorisation de m : m=a*q+r => q = int[m/a] et r = m (mod a)
On obtient : q = 127773
r = 2836
En
utilisant de façons différentes ces quatre variables (par
multiplication croisées, minimisation de l’ordre de
corrélation entre différentes génération de
séquences, par addition et normalisation, ou bien soustraction
pour Ran3) on obtient les différents générateurs
Ran0, 1, 2, 3.
Les
générateurs Ran0 et Ran1 renvoient un nombre compris
entre 0 et 1 avec une période comprise entre 108 et 109 termes.
Quant
aux fonctions Ran2 et Ran3 elles fonctionnent sur le même
principe mais avec d’autre nombres premier ce qui a pour effet
d’augmenter leur période à 1018 termes.
La fonction « gasdev » :
La
fonction gasdev utilise la « méthode de
Box-Muller », qui consiste à utiliser un changement
de variables aléatoires. A partir d’une distribution
uniforme X=1 pour x = [0..1], on souhaite obtenir une
distribution gaussienne
Cette méthode utilise la formule de changement de variable aléatoire
Considérant
la transformation entre deux variables uniformes x1 et x2 sur [0,1] et
deux variables y1,y2 on peut écrire :
Et donc :
On en déduit le déterminant du jacobien :
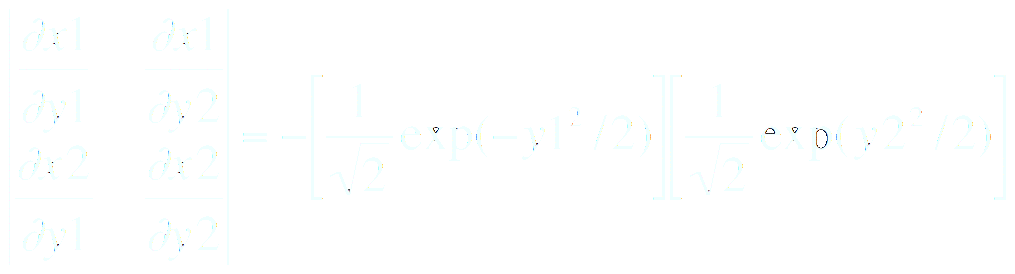
Nous retrouvons bien une distribution gaussienne.
La fonction Jacobi (Diagonalisation de matrices symétriques) :
L’approche
théorique de cet algorithme est basée sur un principe de
« rotation » des coefficients de la matrice
à diagonaliser. La rotation de Jacobi est une matrice de la
forme :
Soit A, une matrice symétrique à diagonaliser, on fait l’opération :
on obtient :
les indices (p,q) étant ceux du coefficient apq à éliminer et c et s vérifient l’équation
Cette
opération sera réitérée plusieurs fois afin
d’obtenir des zéro sur les termes qui ne sont pas
diagonaux.