Holographie d'un objet complexe
Principe
Un objet complexe se comporte comme un ensemble de points. Pour illustrer le principe de l'holographie d'un objet complexe, nous avons simulé l'hologramme d'une barre composée de 10 points:
Lorsque l'on fait la simulation numérique de l'hologramme de ces 10 points on obtient une image du type:
La transformée de Fourier (le module) appliquée à ces franges présente l'allure suivante :
On remarque que la partie encadrée en rouge en bas à droite correspond à l'image de l'objet. Chaque point de l'objet réel crée trois pics sur cette image.
L'objet complexe se comporte bien comme un ensemble de points. Le flou observé sur les images gauche et centrale est dû au fait que l'ensemble des points ne soit pas dans le même plan que la source.
Holographie numérique d'un trombonne
On procède de la même manière que pour Holographie d'un objet ponctuel en remplaçant seulement la tête d'épingle par le trombonne ci dessous.
La source de référence et le trombonne sont dans le même plan (à 40 cm du capteur CCD).
L'image ci-dessous est une photographie du système de franges réalisé avec le capteur CCD.
La transformée de Fourier (le module) appliquée à ces franges présente l'allure suivante :
Nous avons en fait sommé 200 transformées de Fourier afin de diminuer le bruit aléatoire.
On aperçoit deux fois l'image virtuelle du trombone ainsi que la tache centrale correspondant à la source.
Calcul des dimensions et du relief
Nous montrerons dans ce paragraphe qu'il est possible de retrouver les 3 dimensions d'un objet à partir d'un seul hologramme.
Les dimensions de l'objet dans le plan parallèle au capteur s'obtiennent à partir de la transformée de Fourier de l'hologramme.
Comme vu dans l'holographie d'un objet ponctuel nous pouvons donc déterminer la distance séparant un point de la source. Pour cela, il suffit de faire les différences U2-U1 et V2-V1.
La dimension de l'objet selon x est donné par la formule :
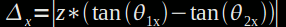avec 
, 
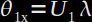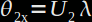et
La dimension de l'objet selon y est donné par la formule :
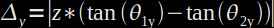avec 
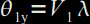et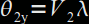 
A.N. : Δx = 1,5mm. La valeur mesurée à la règle 2mm +/-1 mm.
Δy = 4,1mm. La valeur mesurée à la règle 4mm +/-1 mm.
Pour trouver la dimension de l'objet dans le plan perpendiculaire au capteur nous devons voir l'objet sous différentes perspectives. Ce qui est le cas aux extrémités du capteur CCD.
En effet en prenant une partie de l'holograme à chaque extrémité du capteur CCD, il est possible d'apercevoir l'objet sous 2 perspectives différentes et donc de calculer la profondeur de l'objet.
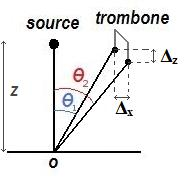
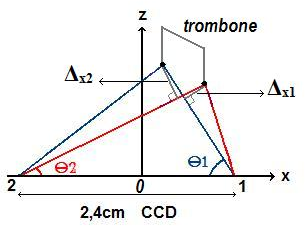
Nous pouvons calculer Δz en projetant sur l'axe z la distance X apparente.
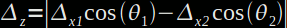avec Δx1, Δx2, Θ1 et Θ2 tel que défini ci-dessous.
Δz = 2,2mm. La valeur mesurée est de 2mm +/- 1 mm.
Les valeurs calculées correspondent aux valeurs mesurées aux incertitudes, près cette méthode est donc exploitable.