Etude de l'espace des phases

L'espace des phases en mécanique analytique est un espace à 2M dimensions permettant d'interpréter géométriquement le mouvement d'un système mécanique décrit par des équations différentielles du second ordre par rapport au temps. Il est étroitement associé aux équations de Hamilton et donc au formalisme Hamiltonien. Les 2M dimensions correspondent aux M paires de variables conjuguées intervenant dans les équations différentielles gouvernant le mouvement d'un système mécanique ce qui est ici notre cas.
Cet espace est fondamental en physique et on le retrouve au coeur de la formulation de la mécanique quantique et de la mécanique statistique.



• Section de Poincarré



• Définition

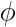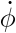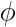Pour définir cette section de Poincaré dans le cadre du problème qui nous concerne , on est ici dans un espace avec quatre paramètres variables qui sont , point, et et on ne peut pas représenté un espace à quatre dimensions. Il est alors intéressant de reporter sur un diagramme les valeurs (,) de notre masse à chaque fois que celle ci coupe l'axe en sin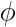(modulo 2 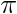) s'annule et on ne garde que les valeurs , correspondant a ce moment précis. Ce qui nous ramène a 2 dimensions notre pendule. Cela nous permettra de faire des portraits de phase du pendule donc de pouvoir étudier son état.

• Tracés de portraits de phases
Petites oscillations

Notre simulation considère ici un système sans pertes d'énergies(pas de frottements)et de plus l'on sait que les oscillations libres, non amorties, de faible amplitude sont quasi sinusoïdales. D'ou notre intérêt de les simuler.
en fonction de


• a)Pendule simple


La simulation a été faite pour différents angles de =3.15 radians à =3.15/200 radians.
Ici on a choisi une vitesse φ et un angle alpha tous deux nuls. Cela équivaut donc à un simple pendule pesant. La lecture des coordonnées de notre pendule M de l'espace des phases donne directement la vitesse et la position du mobile. Pour =3.15 radians La trajectoire décrite par M donne l'évolution du système au cours du temps. On peut reconnaître les quelques caractères généraux : - lorsque l'oscillateur est amorti donc perd de la vitesse du fait de la pesanteur, la trajectoire converge inexorablement vers un point,de l'axe des abscisses il s'agit là des positions d'équilibre du système(==-).
Lorsque l'oscillateur est entretenu, la trajectoire converge vers une trajectoire limite, correspondant à un régime permanent (cycle limite).On a une vitesse a son maximum donc toute l'énergie du système est sous forme d'énergie cinétique.
Pour toutes les autres valeurs de prises on remarque que dans l'espace de phase on a des cercles ce qui veut dire que les oscillations de notre système sont sinusoïdales.
Figure 1 : Portrait de phase d'un pendule pesant simple.

• b)Pendule tournant avec un angle d'inclinaison


-Cas simples
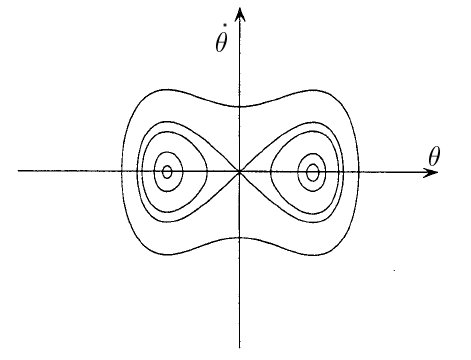
Les trajectoires sont fermées, le mouvement est donc périodique
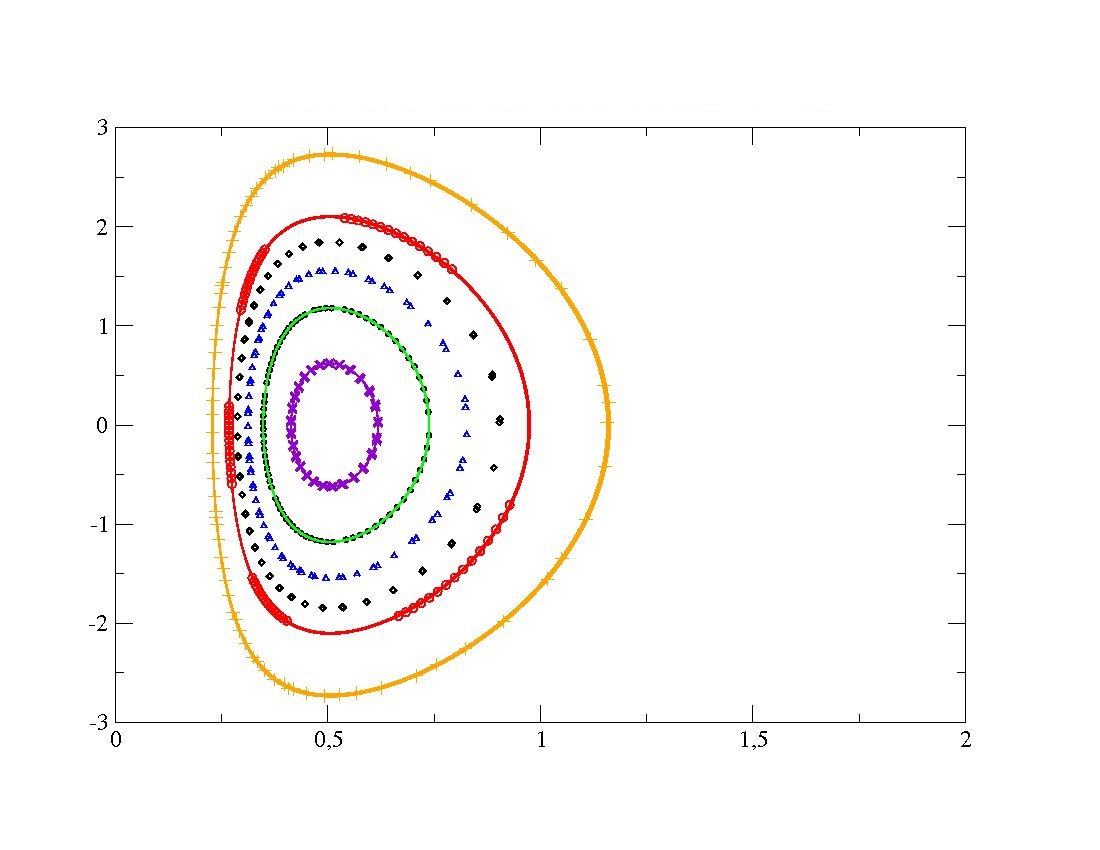
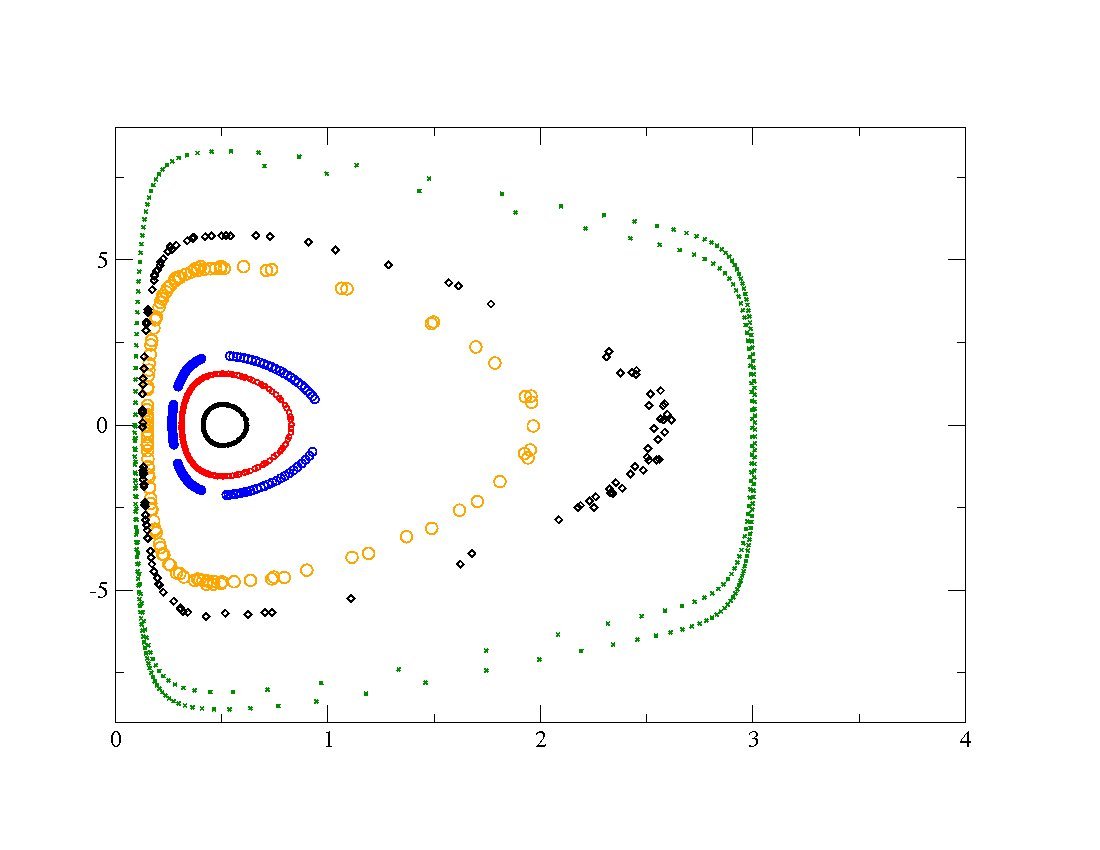
On fixe ici une vitesse de rotation 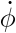= 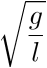et on a un angle de =0,52.
Cela équivaut à la pulsation de notre pendule(petites amplitudes). A différentes énergies on obtient le portrait de phase suivant : On observe sur ce portrait de phase on voit que la trajectoire converge à chaque fois vers un point et plus on augmente notre énergie et plus le point en question est tr&eagrave;s prononcé .Le point de convergence que l'on observe est une solution homocline de nos équations en effet à un temps t tendant vers plus l'infini ou moins l'infini le portrait convergera vers ce point.Cela corespondrait au portait de phase de la figure 4 representée en dessous. Mais à une certaine valeur d'énergie on a un portrait à trajectoire limite sans point de convergence.Celle ci reste malgré tout une trajectoire fermée cela nous rappele le portrait de phase au point de bifurcation entre deux équilibres instables que l'on a pu étudier lors de notre Travail pratique(pendule inversé en l=lc)


Figure 2 et 3 : Portrait de phase d'un pendule tournant incliné.

Figure 4 : Portrait de phase d'un pendule tournant avec des petites oscillations. -Cas extrêmes
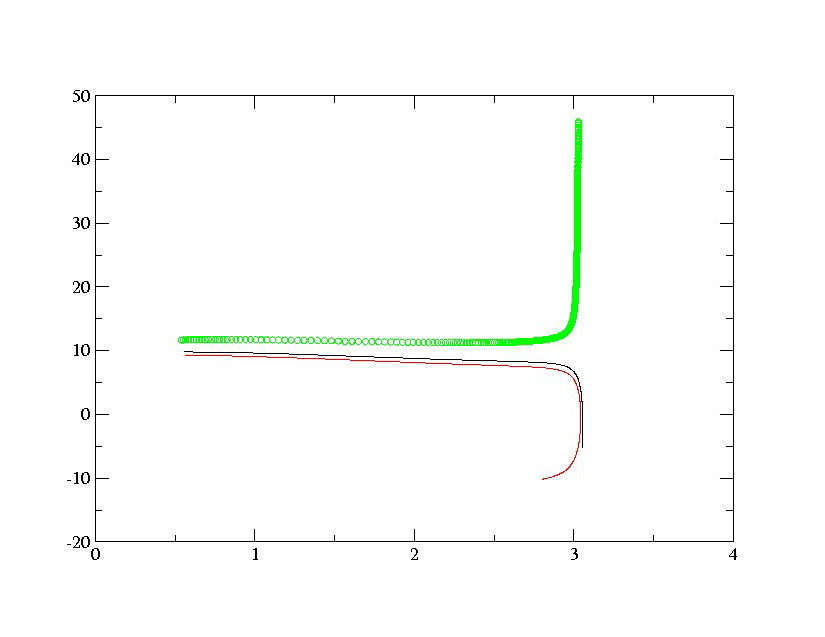
La figure de gauche représente le portrait de phase de notre pendule avec les paramètres de départ suivants := /6, =0.5,et Em=25.On voit clairement que ce système n'a pas de trajectoire limite car il une croissance linéaire de la vitesse et de l'angle .A des énergie encore plus élevées on obtient la figure 7 en rouge avec Em=50 joules et en vert Em=80 joules.On voit clairement des phénoménes étranges de l'un a l'autre.Les portraits de phases obtenues ne ressemblent en rien a ceux que l'on voit habituellement et les directions sont elles aussi aléatoires.Celui avec une énergie Em=50 joules décroit tandis que celui avec une énergie Em=80j croit.Bien que malgré cela on voit bien que le système voit son angle limité en 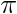ce système n'en reste pas moins instable du fait qu'il n'a pas de point de convergence et nous supposons chaotiques.
Le graphique de droite lui nous montre le portrait de phase du même système que précédemment sauf qu'ici nous avons une énergie Em=1,4.On voit ici que avec une telle valeur d'énergie le pendule est incapable de ne faire ne serait qu'un seul tour complet.
Lorsque l'on fixe , , et Em le seul paramètre qui puisse varier restant est . Ainsi pour observer des oscillation il faut veiller à ce que pour ce système la valeur d'énergie mécanique (donc de )soit suffisamment grande comme mais pas trop sinon on obtient un système incapable de faire une oscillation donc sans grand int&ecute;rêt.

Figure 5 et 6 : Portrait de phase d'un pendule tournant incliné dans les cas extrêmes.
A gauche:avec une énergie mécanique très élevée
A droite:avec une énergie mécanique très faible
. . Figure 7.


• c)Comparaisons aux résultats théoriques


Grâce aux vecteurs de position et de rotation de notre pendule on obtient un moment angulaire:





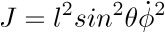
Cela nous donne donne l'expression de 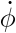telle que :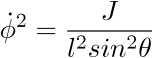




On remplace cette derni&eagrave;re par son expression dans l'équations trouvées avant



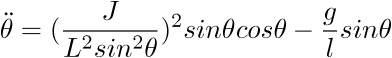
Puis en mutipliant cette équation par 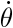puis en intégrant on obtient une éxpréssion: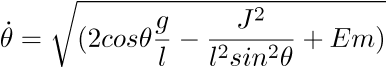




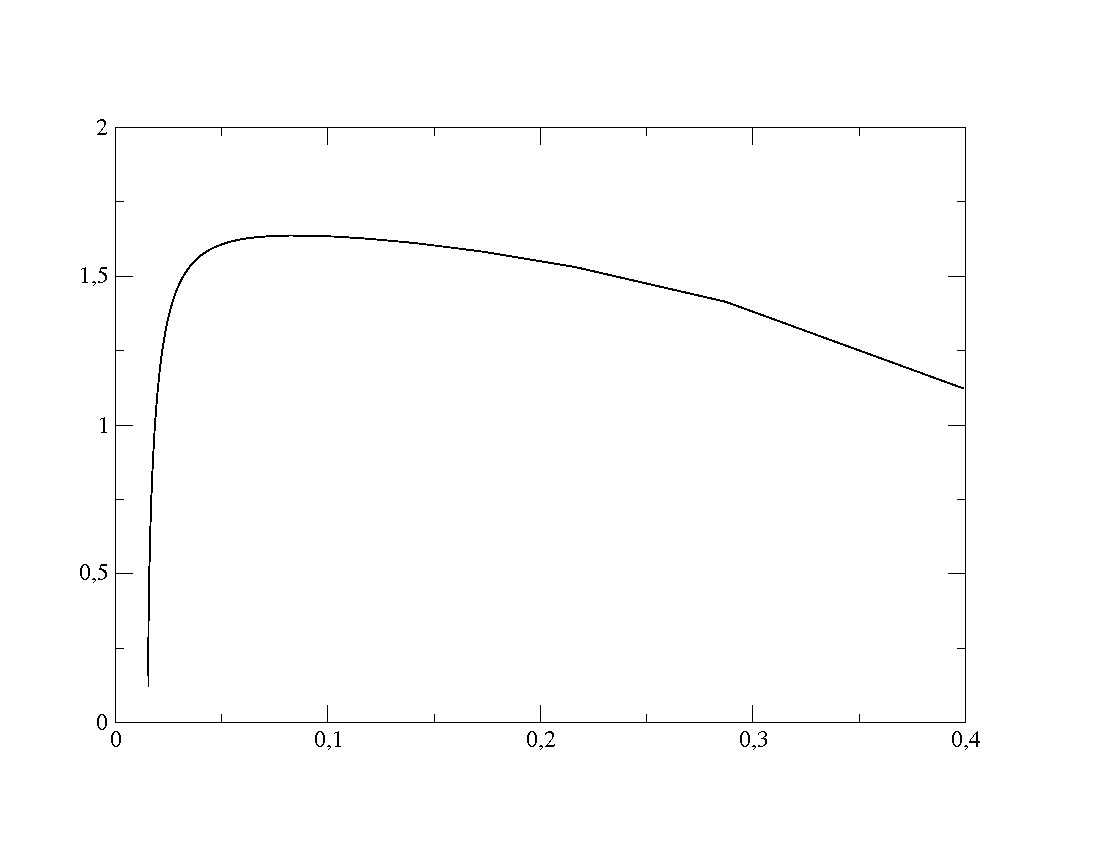
Après avoir obtenu les différents résultats cités précédemment nous vérifions ceux ci à l'aide de la formulation théorique. Grâce á cette fonction nous dessinons le portrait de phase théorique suivant :




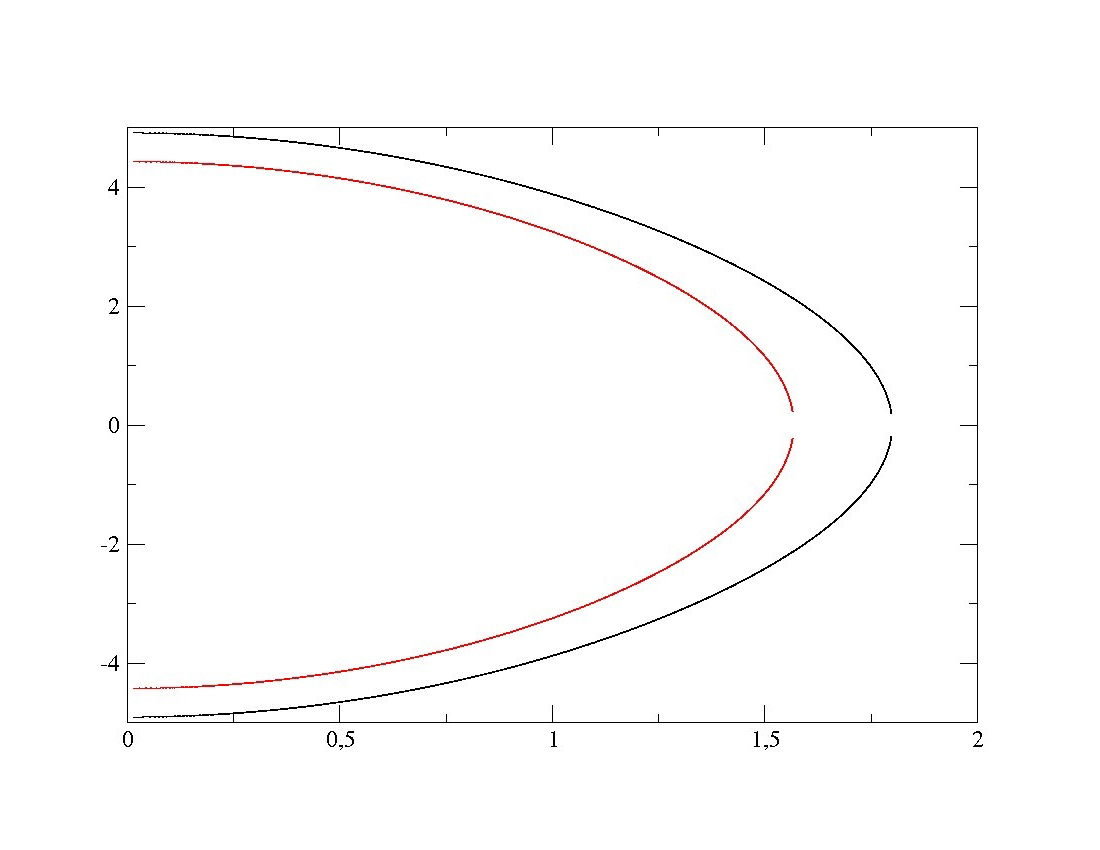
On constate une similitude très prononcée entre ce portrait de phase et ceux dans le cadre simple à petits angles repréntés le long de notre site.
PS:Les conditions de simulations ici ont été choisie de sorte qu'elles soient les plus proches de celle des simulations précedentes.Les points proches de zero n'ont pu ètre représentés car le logiciel ne pouvait le faire nous nous en excusons.





AKOUALA-RARIJAONA