Annexe - calcul des points auto-focaux
On suppose l' existence d' un point auto-focale le long d' une trajectoire diagonale. Celui-ci se situe à une distance δ de la première réfléxion. On construit alors une nouvelle matrice de transfert suivant la logique schématisée ainsi :
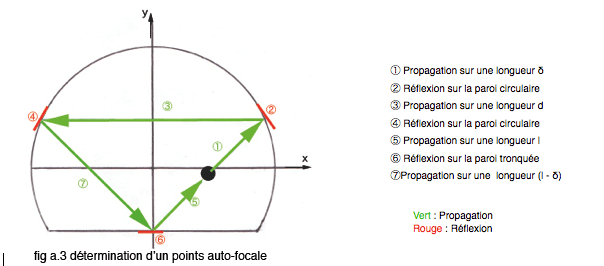
Il suffit dès lors de chainer les matrices (2.4.2) dans l' ordre schématisé. On obtient en replaçant directement par les valeurs numériques:
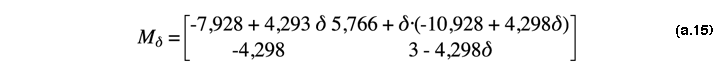
Le terme suivant :
![]()
Doit être nul afin de caractériser une densité de rayon infinie. C'est un polynome de second degrés, on obtient 2 solutions pour δ. Seulement une des deux est supèrieure à la longueur de la trajectoire diagonale, ce qui est impossible compte tenu des hypothèses posées. Soit :
![]()

