Annexe - caractéristiques de l' OP3
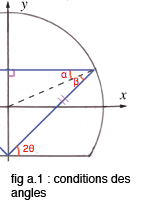
Les lois de la réfléxion impose α = β. De plus pour former un triangle isocèle, il est nécessaire d' avoir 2θ = α + β. Soit α = β = θ.
Il existe un point M qui appartient à la trajectoire diagonale et qui appartient aussi au cercle de rayon unité et de centre origine dans la région des x positifs. Ces conditions s' écrivent :
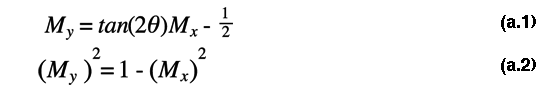
Il apparait dès lors judicieux d' écrire l' expression (a.1) au carré et d' y injecter (a.2). Il suffit ensuite de résoudre un polynome de degrés 2.
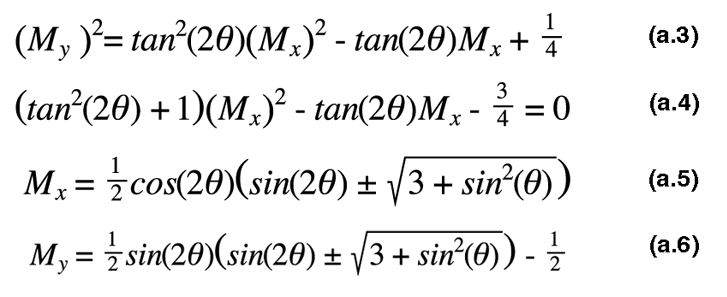
Dés lors on peut créer deux vecteurs ainsi:
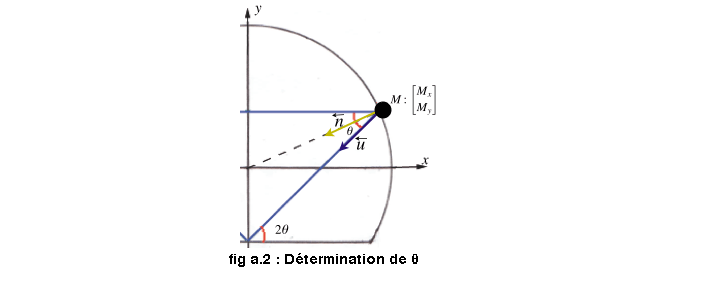
Le produit scalaire des deux vecteurs est par construction égal à cos(θ) d'où :
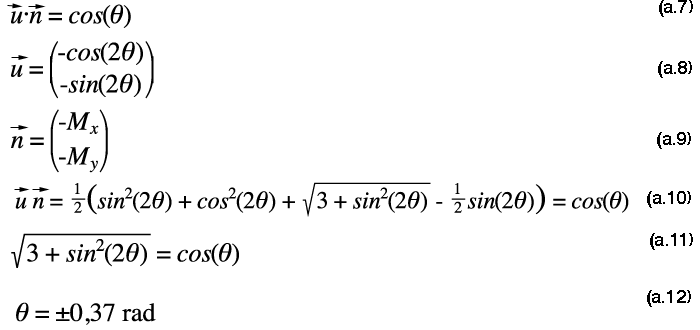
Les longueurs qui suivent se déduisent aisement par trigonométrie et par le théorème de Pythagore.

