Simulation - Propagation dans une fibre optique classique
On rappelle que la lumière est une onde se propageant, l' évolution du champ éléctrique dans une fibre optique est régie par l' équation d' Helmholtz. On écrit alors l' équation régissant l' évolution du champ éléctrique ainsi :

La fibre optique possède deux indices, celui du coeur et celui de la gaine optique. Afin d' assurer la propagation dans la fibre optique, l' indice du coeur est plus élevé que celui de la gaine :
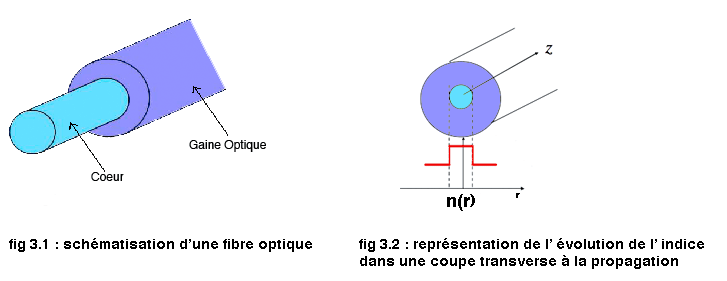
Or, on schématise la propagation ainsi :
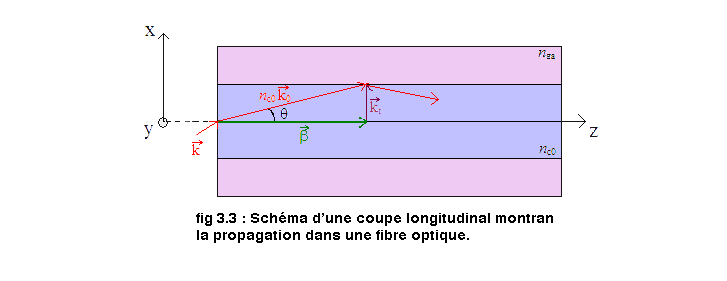
On décompose dès lors le vecteur d' onde comme une composante tranverse kt appartenant au plan (O,x,y) et une longitudinale β représentant la propagation suivant l' axe z.
On remarque que si l'on projette la propagation sur la section transverse de la fibre, on retrouve une évolution des rayons analogues à celle de rayons géométriques qui se réfléchissent sur les contours d' un billard en forme de cercle.
En vue de la symétrie du problème, les coordonnées cylindriques semblent plus appropriées. L' équation d' Helmotz devient :
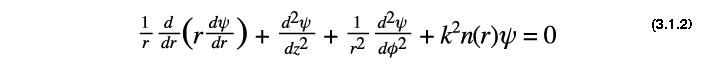
La fonction ψ est a variable séparable, de telle sorte que l' on peut poser une solution sous la forme :
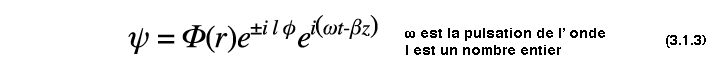
L' équation devient dès lors :
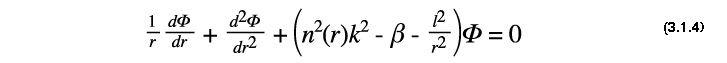
Les solutions analytiques de ce problèmes sont des fonctions de Bessel soit :
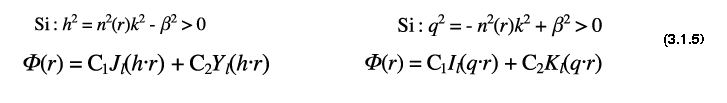
On remarque que la fonction Φ possède un indice l. A chaque valeur de l est associée à ce qu'on appelle un mode de propagation. Il existe de plus des conditions de continuitées pour la fonction Φ et sa dérivée aux interfaces. Ces conditions imposent dès lors une quantification de la valeur de kt. On peut donc discrétiser la valeur de kt. A chaque valeur de kt est associé un mode de propagation. La solution générale est une combinaison linaire des modes trouvés, soit :
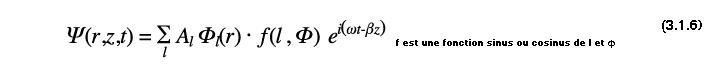
Les différents coefficients Al correspondent au poids qu'impliquerait une condition initiale donnée sur chaque mode. Afin de retrouver les coordonnées du vecteur d' onde transverse à la propagation de l' onde dans le plan (O , x , y), il est nécessaire de passer par l' espace des fréquences spatiales. La transformée de Fourier est alors un outil essentiel pour retrouver les modes de propagation. Dans les représentations des futures simulations, on montrera alors le champ proche à côté du champ lointain. Le champ proche est l' intensité du champ à la sortie de la fibre. Le champ lointain est l' intensité de la transformée de Fourier du champ à la sortie de la fibre.


