Simulation - Faisceau gaussien simple -1
La première approche des simulations sera simplement d' envoyer un "faisceau gaussien" dans la fibre optique en ciblant un point auto-focale. Comme on l' a déjà vu en partie géométrique ces points sont caractéristiques de l' orbite triangle. La simulation ce fait sur une largeur de fenêtre de 128 pixels. Le rayon de la fibre étant 89% de 64 pixels (56.96 pixels). Nous utiliserons donc le pixel comme unité pour les longueurs caractéristiques dans la fibre optique. De plus la propagation ce fait sur une fibre optique longue de 8 cm.
Un faisceau gaussien possède une intensité dont le profil suit une loi de Gauss, soit :
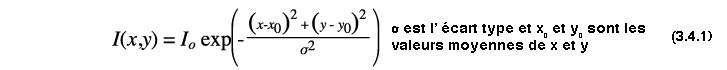
Dans les simulations qui vont suivre, l' action se fait suivant la position de la gaussienne dans la fibre optique et la largeur σ. En jouant sur ces différents paramètres, on éspere retrouver une trace de l' orbite triangle.
Seulement avant tout, il apparait utile de montrer le comportement de la fibre optique tronquée pour une situation quelconque. On remarque que si l' on envoie un faisceau gaussien sans viser de point auto-focale on obtient une figure de "grain" ou "speckle". Celle-ci est représentative de la nature chaotique de la fibre optique :
En observant le champ proche et lointain côte à côte on ne trouve aucune direction de propagation particulière. Ceci est comme déjà dit, caractéristique de la nature chaotique de la fibre optique tronquée.
On étudiera maintenant la propagation lorsque l' on cible un point auto-focale. Les simulations qui suivent ce font suivant les points auto-focaux n de la figure 2.6. Le choix de ces points en particulier est motivé par des soucis pratiques qu'on explicitera pour les simulations suivantes. On excite donc la fibre optique en entrée par un faisceau dont l' intensité possède un profil Gaussien comme schématiser ici :
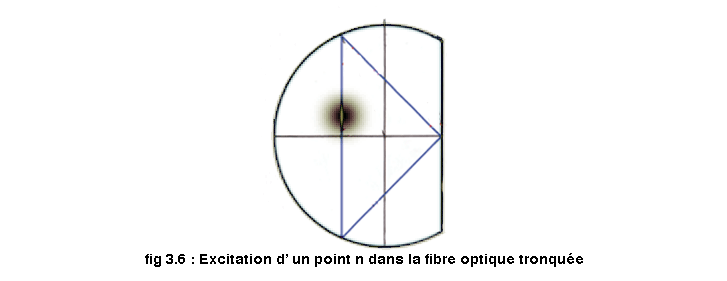
On y associe ces figures des poids des mode en fonction de kt pour différentes largeurs de gausiennes :
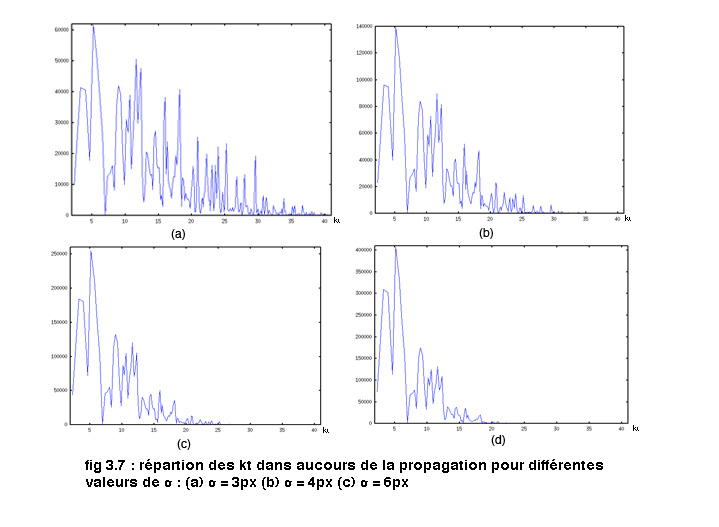
On remarque que plus la largeur de la gausienne est grande plus on séléctionne des modes proches du fondamental. On rappelle que le fondamental de l' OP3 est ici la valeur la plus basse des kt correspondant à un mode particulier. Que ce même fondamental reste présent pour toutes les simulations et que le poid de celui-ci augmente plus σ est élevé. On remarque qu'il existe plusieurs structures périodiques. Il est cependant trop tôt pour en déduire que nous avons bien séléctionner les kt recherchés. En effet, il semble difficile de déceler la présence des valeurs recherchées, puisqu'il semble que nous ayons excité de nombreux modes différents. On ne peut donc pas observer clairement les kt associés à l' orbite triangle.


