Simulation - Faisceau gaussien modulé -1
La première approche des simulations ayant montré ses limites, il est nécésaire d' ajouter certains paramètres pour caractériser plus efficacement l' orbite triangle. Cela afin de sélectionner une figure des kt plus représentative de l' orbite triangle.
Comme le titre le laisse supposer, on ajoute une modulation au faisceau gaussien. Dès lors on comprend le choix des points n en particulier. Ceux-ci étant situés sur une trajectoire diagonale la modulation ce fait uniquement suivant l' axe des abscisses. Les caractéristiques des longueurs de la fibre optique et de son rayon restent inchangé.
L'idée dans ces nouvelles simulations est de cibler plus efficacement l' orbite triangle. Envoyer un faisceau modulé suivant un kt caractéristique de l' orbite triangle est donc une solution.
On envoie dès lors, toujours sur le même point n une faisceau Gaussien modulé suivant plusieurs valeurs des kt calculées respéctant l' équation (3.2.3). On fixe la largeur de la gaussienne à σ = 8 pixels. Pour un k modulant tel que k = 14.3 on obtient la propagation suivante :
Cette fois-ci, on remarque que l'intensité suit majoritairement une trajectoire particulière. Force est de constater que cette trajectoire est de forme triangulaire.
Après la visualisation de la propagationle long de la fibre, on lance de nouvelles simulations en changeant la valeur du k modulant la gausienne. Il est maintenant nécessaire d' y ajouter l' analyse des kt. Pour cela on aura encore recours à la représentation du poids des modes en fonction des kt :
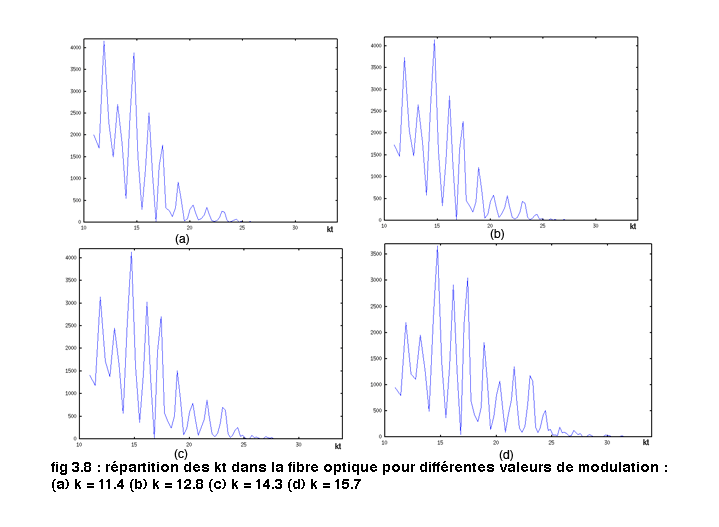
Ici la structure est nettement périodique. On peut donc mesurer le décallage Δkt trouvé dans les simulations et les comparer avec les résultats déjà trouvés (equation 3.2.4). On résume le tout dans le tableau suivant :
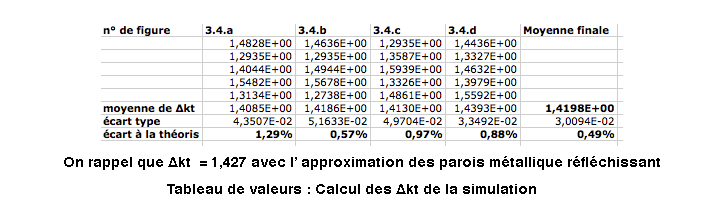
Les valeurs trouvées sont très proches du résultat de l' équation (3.2.4). On a donc bien mis en évidence l' existence de ce mode dans la fibre optique possédant à la base une géométrie chaotique.


