Simulation - Condition de cavité résonnante
On rappelle que l' on recherche des modes particuliers associés à l' orbite triangle. Pour cela, il est nécessaire que les ondes incidentes et réfléchies soient en phase, c'est une condition d' interférence constructive. Ou, par analogie avec une cavité optique, c'est une condition de cavité résonnante. Dans la suite de l' étude on assimile les contours de la fibre optique à des paroies metaliques réfléchissantes. On schématise la condition de résonnance tel que :
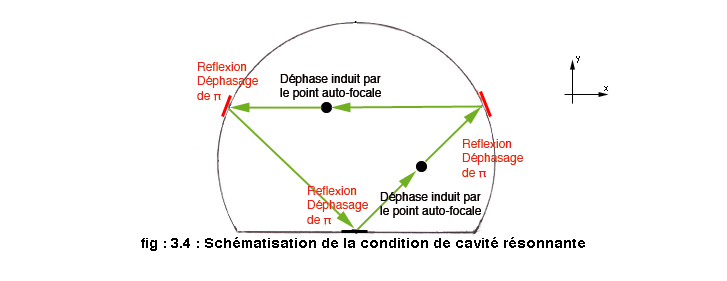
Ainsi le déphasage doit être un entier multiple de 2π, soit :
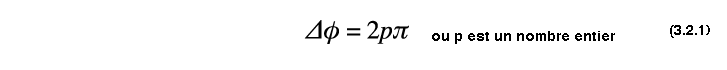
Il existe, le long du trajet un déphasage du au parcours de l' onde, celui-ci est :
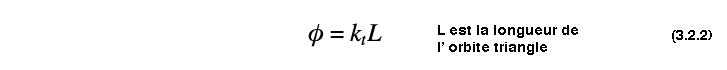
De plus, à chaque réfléxion sur une paroi ,comme montrée sur la figure 3.4 , l' onde est déphasée de π soit 3π au cours de l' orbite périodique. Ce résultat étant du à l' assimilation des contour de la fibre optique à des parois métalliques réfléchissantes. Finalement on obtient :
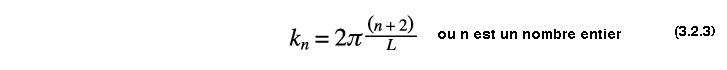
Le terme π, en plus du déphasage engendré par les réfléxions, est du à la présence de 2 points auto-focaux lors du trajet de l' onde. Ceux-ci refocalisent la lumière et ajoute, pour chaque point auto-focale, un terme π/2 dans le déphasage.
Il est a noter qu'il existe au cours d'une trajéctoire de l' OP3 seulement deux points auto-focaux, bien que dans la partie précédente, on en ait défini quatre. La condition d' accord des phases le long de l' orbite périodique impose le choix d' une trajectoire donnée. Le calcul des points auto-focaux quand à lui prend aussi en compte la trajectoire dans le sens opposé. Pour être plus précis, la figure 3.1.4 représente une trajectoire. On peut très bien imaginer une autre trajectoire en inversant le sens des abscisses, dans ce cas on verrait apparaitre les deux autres points auto-focaux représentés dans la partie géométrique. Le fait est qu' au cours d' une trajectoire périodique de l' OP3, on rencontre seulement 2 points auto-focaux.
On définit la constante associée aux kt suivante :
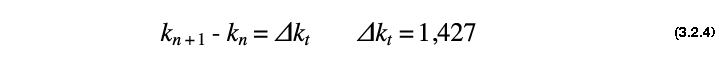
Ainsi, si l' on retrouve une structure périodique, dans une représentation des kt, se répétant tout les Δkt c'est que l' on a bien à faire à l' OP3. C'est sur ce résultat, en continuité directe avec l' étude géométrique, que l' on basera le traitement de données numériques obtenu par la simulation.


