Simulation dans une fibre multimode
Dans un premier temps, le code calcule la phase directe du faisceau qui s'est propagé dans la fibre.
Calcul direct de la phase:
L’expression du champ à la sortie de la fibre peut se mettre sous la forme : ψ = A exp( i φ ) .La phase est donc donnée par : φ = arctan (Im (ψ) / Re (ψ)) , où les parties réelle et imaginaire du champ sont extraites directement d'une simulation numérique.
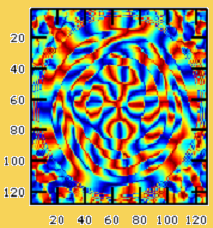
FIG 5.1: Figure représentant la phase d'une onde, calculée directement, en sortie d'une fibre optique multimode
Phase obtenue à partir des interférences:
Le code simule ensuite les interférences entre le champ dans une fibre et un faisceau gaussien.
Il calcule l'intensité totale due aux interférences qui fait intervenir un terme de phase totale.
Cette intensité totale est donnée par :
La phase totale (kh - Φg) fait intervenir deux termes de phase:
- la phase du faisceau gaussien qui s'est propagé, ceci est une phase connue égale à k*h avec k = 2π / λ et h la distance parcourue par ce faisceau;
- et la phase globale qui nous intéresse Φg correspondant à la phase de l'onde dans la fibre multimode.
La simulation numérique extrait cette phase de l'expression de l'intensité:
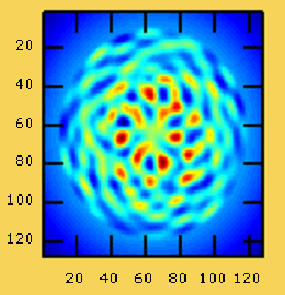
FIG 5.2: Figure d'interférences

FIG 5.3: Figure représentant la phase totale
Pour obtenir la phase de l'onde issue de la fibre, il faut juste soustraire à la phase totale la phase du faisceau qui s'est propagé librement ce qui ne change pas l'allure spatiale de la phase vu qu'elle est uniforme.
Modification de quelques paramètres:
On change les paramètres qu'on peut contrôler du faisceau libre, gaussien, pour voir l'impact sur la phase.
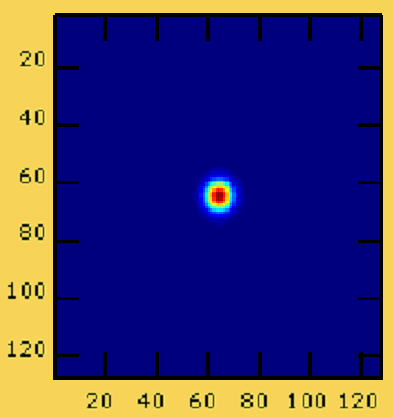
FIG 5.4: Figure représentant l'intensité du bras libre
On commence par modifier la taille du faisceau libre en diminuant la largeur de la gaussienne.
La figure d'intensité ainsi que celle représentant la phase totale se trouvent donc changées et on obtient:
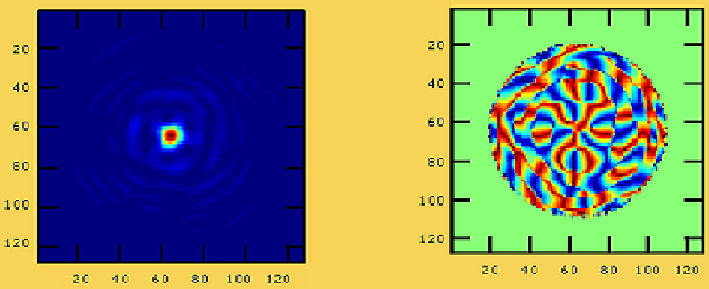
FIG 5.5: Figure représentant les interférences
FIG 5.6: Figure représentant la phase totale
On voit clairement que la phase totale obtenue ne correspond pas à celle calculée directement. Cela explique la raison pour laquelle, dans nos expériences, on cherchait toujours à avoir un faisceau libre plus gros que le faisceau se propageant dans la fibre.
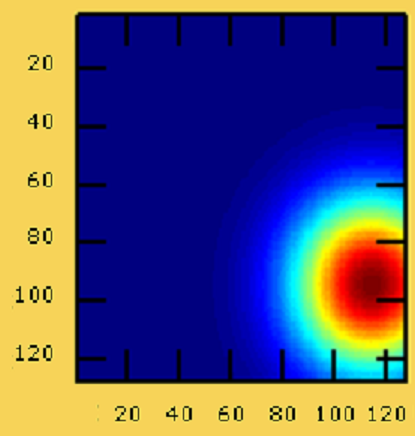
FIG 5.7:Figure représentant l'intensité du bras libre
Maintenant, on fait varier la position du faisceau gaussien de façon à ce qu'il ne coïncide pas avec le faisceau sortant de la fibre.
La superposition des deux faisceaux n'est donc plus parfaite. Ce qui implique que la phase obtenue n'est plus similaire à celle obtenue par calcul direct. C'est pourquoi, lors de la manipulation, il fallait tout aligner et faire en sorte que les deux faisceaux se superposent.
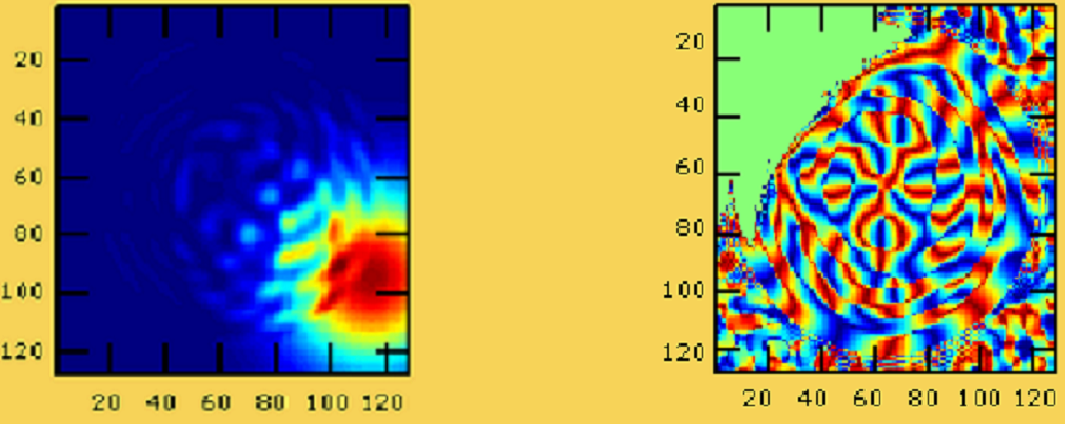
FIG 5.8: Figure représentant les interférences
FIG 5.9: Figure représentant la phase totale
Dans cette partie, on a pu valider le dispositif interférométrique utilisé qui nous a permis de déterminer la phase d'une onde dans une fibre optique multimode. En effet, on a montré que cette phase obtenue en partant des interférences correspond bien à
celle pouvant être calculée directement en numérique. On a pu mettre en évidence, par la suite, l'impact de chaque paramètre sur le rendu expérimental et ainsi montrer que le réglage doit être le plus
parfait possible que ce soit au niveau de l'alignement, de la superposition des deux faisceux, de la taille relative entre ces deux faisceaux.
