Transmission à travers une barrière de potentiel
Dans cette partie, nous détaillons l’étude de l’effet tunnel à travers une simple barrière afin de mettre en évidence les paramètres pertinents à prendre en compte lors de la fabrication des structures. Pour cela, nous nous intéressons aux paramètres qui exercent une influence sur le coefficient de transmission d’un électron à travers cette barrière.
Pour cette étude, nous considérons la structure : ZnO / (Zn,Mg)O /ZnO, illustrée sur la figure 1 :
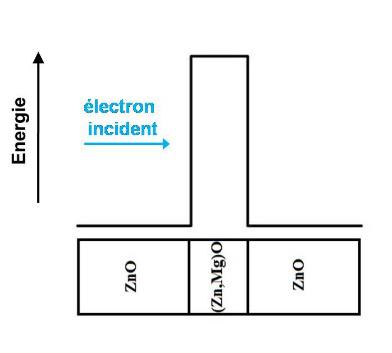 Figure 1 : Barrière de potentiel créée par l’association de semi-conducteurs : ZnO/(Zn,Mg)O/ZnO
Figure 1 : Barrière de potentiel créée par l’association de semi-conducteurs : ZnO/(Zn,Mg)O/ZnO
Pour une structure qui présente une telle géométrie, l’équation de Schrödinger s’écrit :
$$ - \frac{\hbar ^2}{2m} \frac{\text{d}^2\Psi}{\text{d}x^2} + V(x) \Psi (x) = E \Psi (x) $$Avec $\Psi (x)$ la fonction d’onde de l’électron ; $V(x)$ le potentiel qu’il subit, $E$ son énergie, $m$ sa masse et $\hbar$ la constante de Planck divisée par $2\pi$
En séparant la structure en trois régions distinctes correspondant aux trois couches de matériaux ($V(x)$ nul pour ZnO, $V(x)=V_0$ réel positif pour (Zn,Mg)O ), nous obtenons trois solutions que l’on simplifie en considérant seulement l’onde progressant vers les $x > 0$. Ensuite, nous relions nos différentes solutions grâce aux conditions aux limites qui imposent la continuité de notre fonction d’onde ainsi que de sa dérivée.
Ainsi, en posant :
$$ \left\{ \begin{eqnarray*} \kappa ^2 &=& \frac{2m_e (V_0 - E)}{\hbar ^2} \\ k^2 &=& \frac{2m_eE}{\hbar ^2} \end{eqnarray*} \right. $$Nous obtenons le jeu d’équations suivant :
$$ \left\{ \begin{array}{l c l c l c l} A_I &+& B_I &=& A_{II} &+& B_{II} \\ ik A_I &-& ik B_I &=& \kappa A_{II} &-& \kappa A_{III} \\ A_{III} e^{ik a} &+& B_{III} e^{-ik a} &=& A_{II} e^{\kappa a} &+& B_{II} e^{-\kappa a} \\ ik A_{III} e^{ik a} &-& ik B_{III} e^{-ik a} &=& \kappa A_{II} e^{\kappa a} &-& \kappa B_{II} e^{-\kappa a} \end{array} \right. $$
Avec $A_I$, $A_{II}$, $A_{III}$, $B_I$ et $B_{II}$ les amplitudes des ondes selon la région de l’espace qu’elles occupent et de leur sens de propagation et $B_{III}$ nul.
Enfin, en réalisant quelques étapes de calculs supplémentaires, nous obtenons l’expression du coefficient de transmission tel que :
Avec $E$ l’énergie de l’électron, $V_0$ la hauteur de barrière, $a$ sa largeur et $m_e$ la masse de l’électron.
L’expression du coefficient de transmission étant obtenue, nous continuons notre étude en l’appliquant à notre structure. Pour cela, nous réalisons une simulation numérique préalablement validée (cf rapport), en prenant soin de prendre pour masse effective de l’électron, celle qui est propre au ZnO.
Ainsi, en faisant varier l’épaisseur de barrière puis celle de la hauteur (en gardant tous les autres paramètres fixes), nous obtenons les deux courbes suivantes :
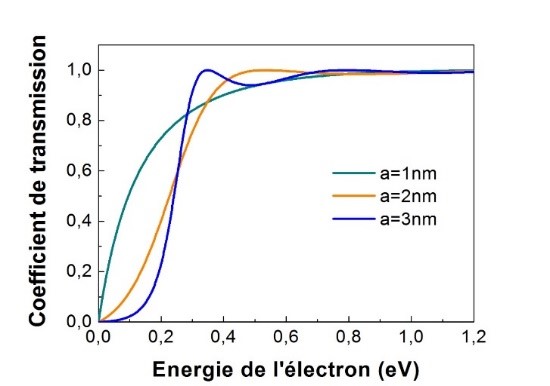
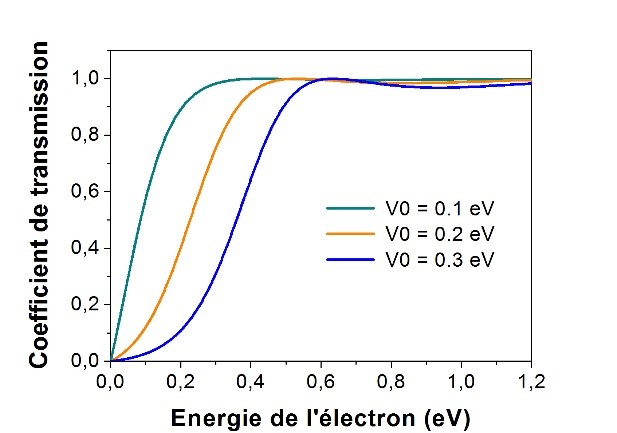 (a)
(b)
(a)
(b)
Figure 2 : Transmission d’un électron à travers une barrière de potentiel en fonction de son énergie.
Cas du ZnO/(Zn,Mg)O – Variation de sa largeur avec V0 = 0.2 eV (a) ; Variation de sa hauteur avec a = 2 nm (b).
De manière globale, la figure 2.a indique que plus la barrière est large, plus la transmission d’un électron avec une énergie donnée sera faible. Lorsque l’épaisseur de la barrière est de 3 nm, très peu d’électrons arrivent à la traverser (coefficient proche de 0 lorsque l’énergie est inférieure à 0.2 eV). Lorsque l’épaisseur est inférieure à 3 nm nous voyons que le coefficient de transmission n’est plus nul pour des énergies inférieures à la hauteur de barrière. La probabilité d’effet tunnel augmente même considérablement pour la barrière de 1 nm d’épaisseur. Au-delà de l’énergie de la barrière (0.2 eV), nous observons sur la barrière la plus épaisse, des oscillations liées à un phénomène de réflexion quantique (encore plus clairement visible sur la figure 2 avec une barrière de 10 nm).
La figure 2.b indique quant à elle une diminution du coefficient de transmission lorsque la hauteur de barrière augmente ; dans ce cas de figure, il faudra fournir plus d’énergie à l’électron pour qu’il puisse traverser la barrière. Plus précisément, lorsque la hauteur de la barrière est de 0.3 eV, la probabilité d’effet tunnel est faible mais non négligeable (jusqu’à 30% des électrons peuvent passer). Elle peut cependant être doublée pour une hauteur de 0.1 eV. Au-delà de l’énergie de barrière (V0), nous remarquons également des variations liées à un phénomène de réflexion quantique mais beaucoup plus faibles que précédemment (figure 2.a), en parfait accord avec la faible épaisseur de barrière utilisée pour cette simulation (2 nm).
Enfin, nous pouvons noter que le coefficient de transmission est très sensible à l’épaisseur et à la hauteur de barrière (qui est directement liée à la composition en Mg de l’alliage). Ces structures vont donc nécessiter une maîtrise extrême (à la monocouche atomique près) lors de leur élaboration. Cette tâche est d’autant plus ardue que nous venons de voir que les barrières doivent être très fine (inférieure à 3 nm) si l’on souhaite bénéficier d’un effet tunnel.