Puits de potentiel et niveaux d'énergies

Nous allons maintenant nous intéresser au cas d'un puits de potentiel obtenu en insérant un matériau de plus petit gap (ZnO) entre deux barrières de potentiel (Zn,Mg)O. Le diagramme de bandes [bande de conduction (BC) et bande de valence (BV)] de ce type de structure est représenté sur la figure1. La faible dimension de ce puits de potentiel (i.e. quelques nanomètres) engendre l’apparition de niveaux discrets d’énergie dans le puits.

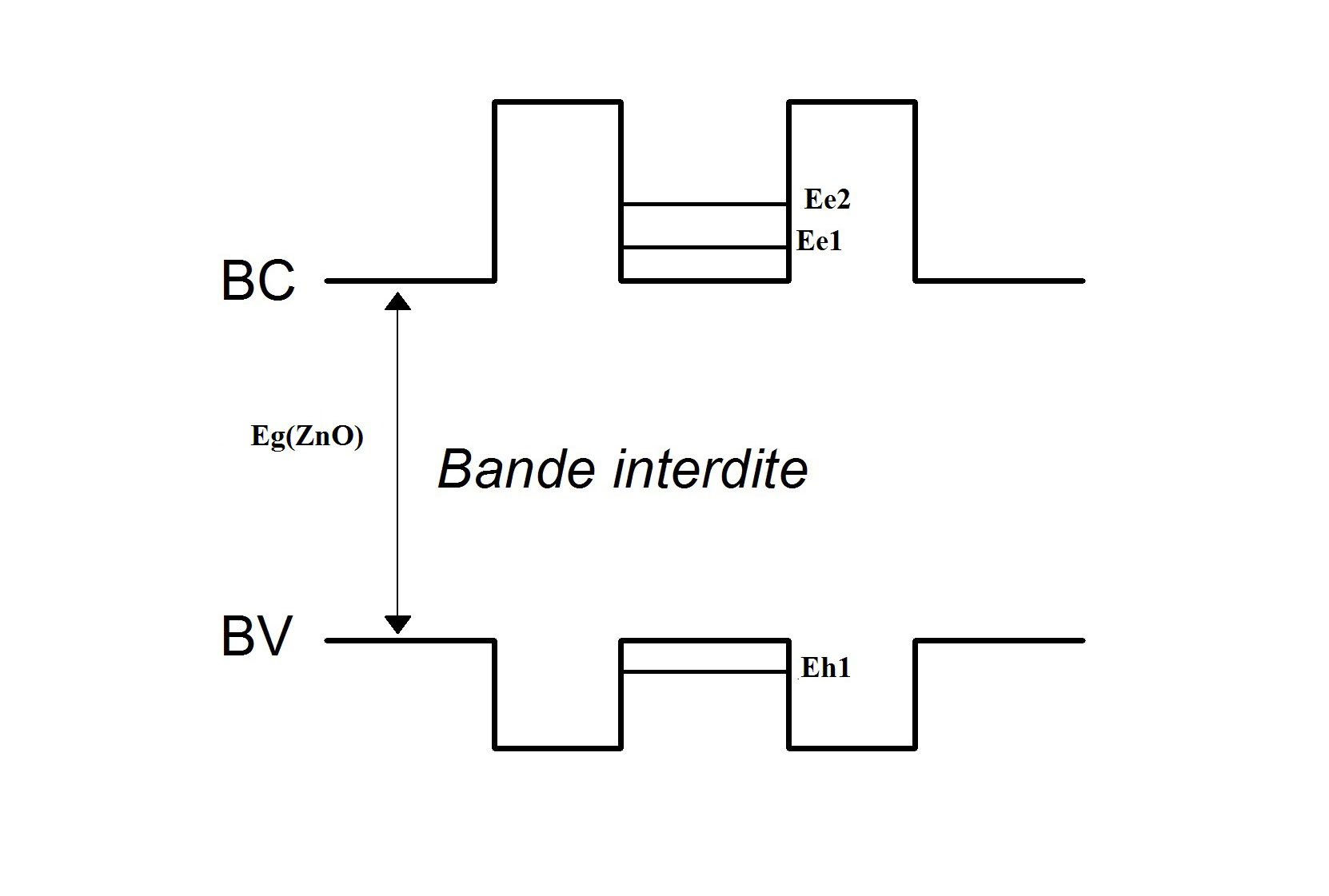Figure 1: Puits de potentiel et niveaux discrets d'énergie occupés par les électrons (Ee) et par les trous (Eh).

L'équation de Schrödinger à laquelle est soumis un électron piégé dans le puits est la suivante:

$$ - \frac{\hbar ^2}{2m} \frac{\text{d}^2\Psi}{\text{d}x^2} + V_0 \Psi (x) = E \Psi (x) $$

En prenant en considération les conditions aux limites et la normalisation de la fonction, on retrouve facilement deux types de solutions:

Solutions paires:

$$ |(cos\frac{ka}{2})|= \frac{k}{k_0} $$

Solutions impaires:

$$ |(sin\frac{ka}{2})|= \frac{k}{k_0} $$

Avec:

$$ V_0 + E = \frac{\hbar ^2 k^2}{2m}         et         V_0 = \frac{\hbar ^2 k_0^2}{2m} $$

Pour résoudre ces équations nous avons écrit un programme Matlab et nous avons obtenu la courbe de la figure 2.
Les solutions sont données par les intersections entre la droite et les fonctions sinusoïdales.
Ces équations n'étant satisfaites que pour certaines valeurs de $k$, donc de $E$, on peut parler de quantification des niveaux d'énergie ou encore d'états discrets d'énergie.

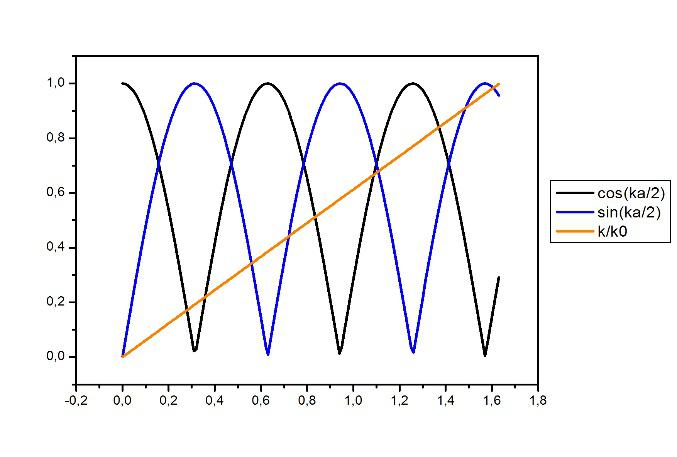Figure 2: Détermination graphique des états discrets d'énergie dans un puits fini dans le cas du ZnO,pour k₀= 1.63 nm‾¹ et un puits de largeur a= 10 nm.

Maintenant qu'on connaît la position des niveaux d'énergie dans le puits, nous pouvons calculer l'énergie correspondante au passage d'un électron du premier état discret de la BC au premier état discret de la BV: $E = E_g + E_{e_1} + E_{h_1}$.
Avec $E_g$ l'énergie de la bande interdite du matériau formant le puits, $E_{e_1}$ l'énergie du premier état discret des électrons et $E_{h_1}$ l'énergie du premier état discret des trous. Nous répétons le calcul pour des puits d'épaisseurs différentes et nous obtenons ainsi la variation théorique de l'énergie de transition $E$ en fonction de l'épaisseur du puits (figure 3).

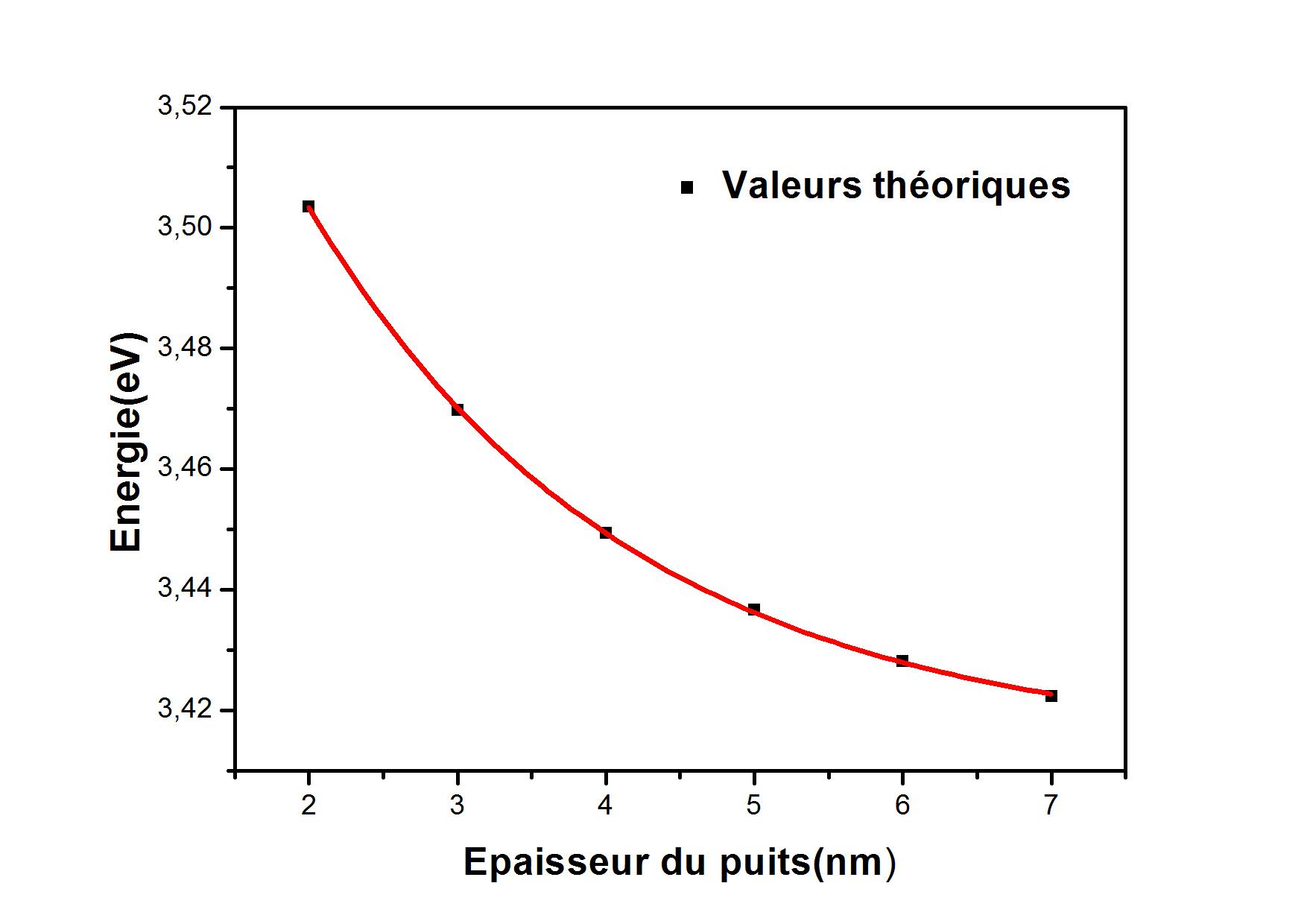Figure 3 : Courbe théorique de l'énergie de transition entre le premier état quantifié dans la bande de conduction et le premier état quantifié dans la bade de valence en fonction de l'épaisseur du puits.