On sait que la mousse a des propriétés d'atténuation du son, c'est pour cela qu'on s'est intéressées à
connaître la longueur d'atténuation (L) qui caractérise notre mousse en fonction des différentes
tailles de bulles. En effet, lorsque l'on rentre le microphone dans le tube rempli de mousse, on
observe que l'amplitude du signal diminue, tout au long du tube.
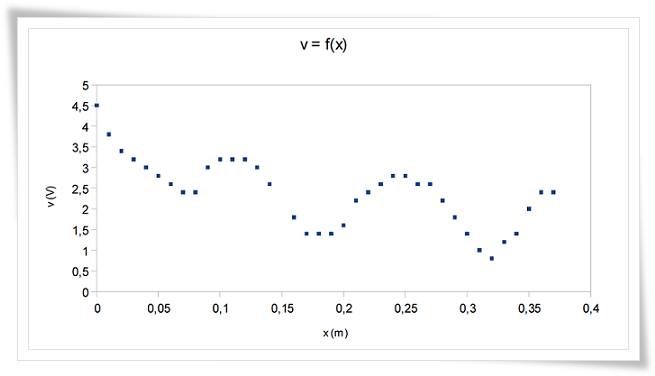On peut remarquer que l'enveloppe de cette onde amortie est de la forme d'une exponentielle
décroissante : y (x )=exp(−x / L ) avec L, la longueur d'atténuation. Les maximas de l'allure de
l'amplitude en fonction de l'espace sont les points de cet exponentiel. On peut donc remonter grâce à
ces informations à la longueur d'atténuation en prenant 2 points de l'exponentielle, à x1 d'amplitude
V1 et x2 d'amplitude V2, L=−x2+x1 /ln( V2/ V1 )
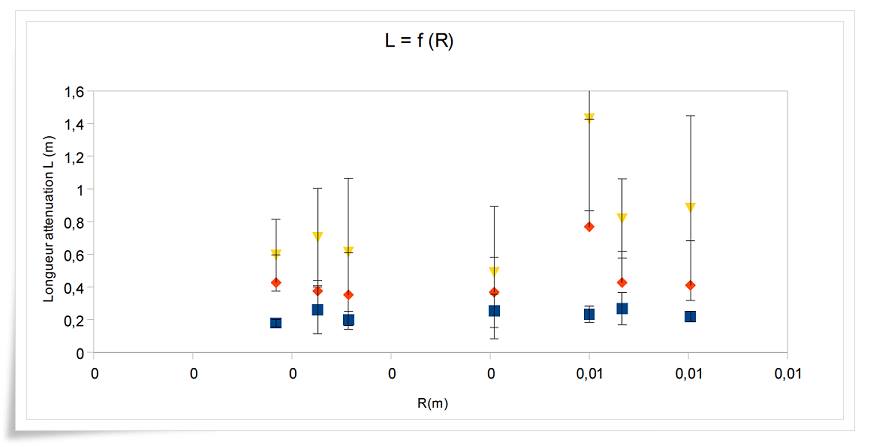les carrés représentent les longueurs d'atténuations calculées avec les minimas, les losanges avec les
moyennes et les triangles avec les maximas.
Nos résultats, notamment les grandes incertitudes, ne nous donnent pas de résultats concrets.
En effet, avec les maximas, les longueurs d'atténuation trouvées, pour une même taille de bulle de
mousse, varient énormément, contrairement aux minimas où les valeurs sont plus rapprochées (on
ne sait pas si ces valeurs sont exploitables ou non, le calcul de la théorie étant plus lourd car il faut
sommer sur une infinité d'onde réfléchies et incidentes...)
Exemple pour R= 2,26 mm on a les longueurs d'atténuations suivantes ;
| Minimas (mm) | Maximas (mm) | Moyennes (mm) |
| 320,6 | 118,9 | 443,1 |
| 240,7 | 311,8 | 394,1 |
| 600,1 | 670,1 | 406,1 |
| 194,8 | 747,1 | 282,9 |
| 232,3 | 974,1 | 417,1 |
| 136,5 | 451,9 | 294,2 |
| 187,3 | 582,6 | 385,1 |
On remarque que les valeurs des longueurs d’atténuation différent largement les unes des autres, on ne peut donc rien en déduire.