Variation
Démarche pour l'estimation de la distance Terre-Lune en prenant en compte les effets de charges.

Calculs de la distance Terre-Lune
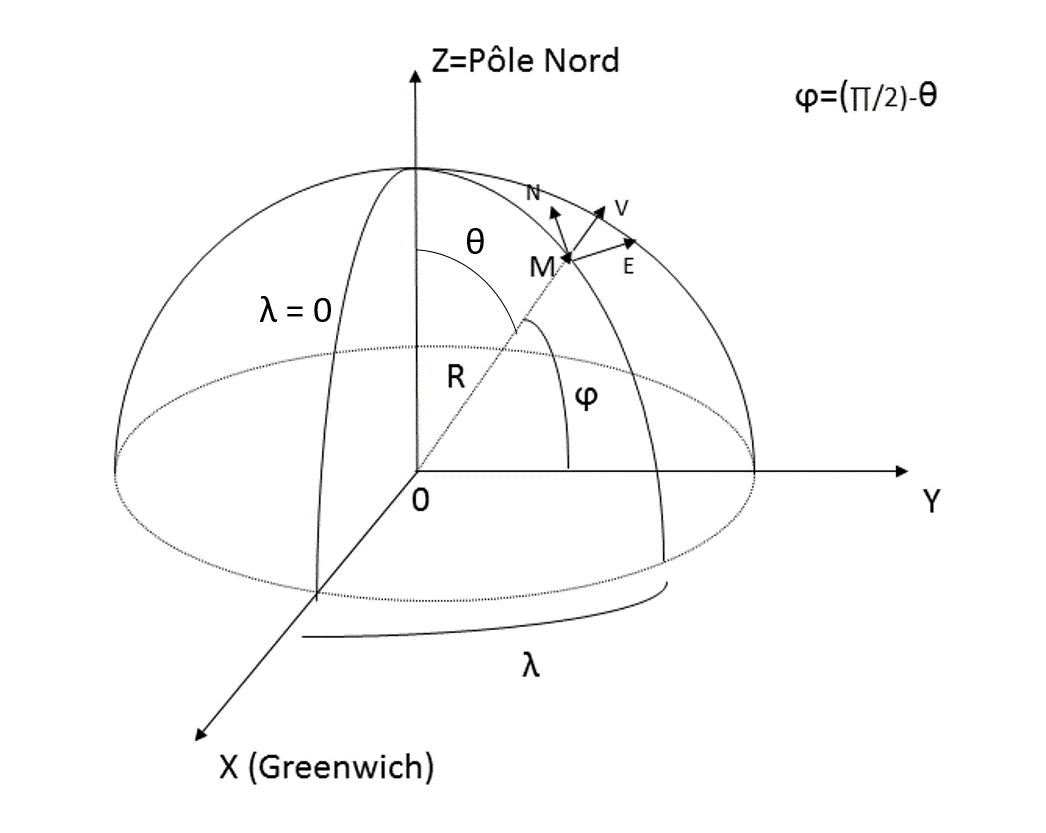
Ci-dessus une figure qui décrit le repère {Est, Nord, Vertical} (où sont issues les données de modèles), dans le repère cartésien {X, Y, Z} (le repère où l'on veut exprimer le déplacement de la station de Télémétrie laser).
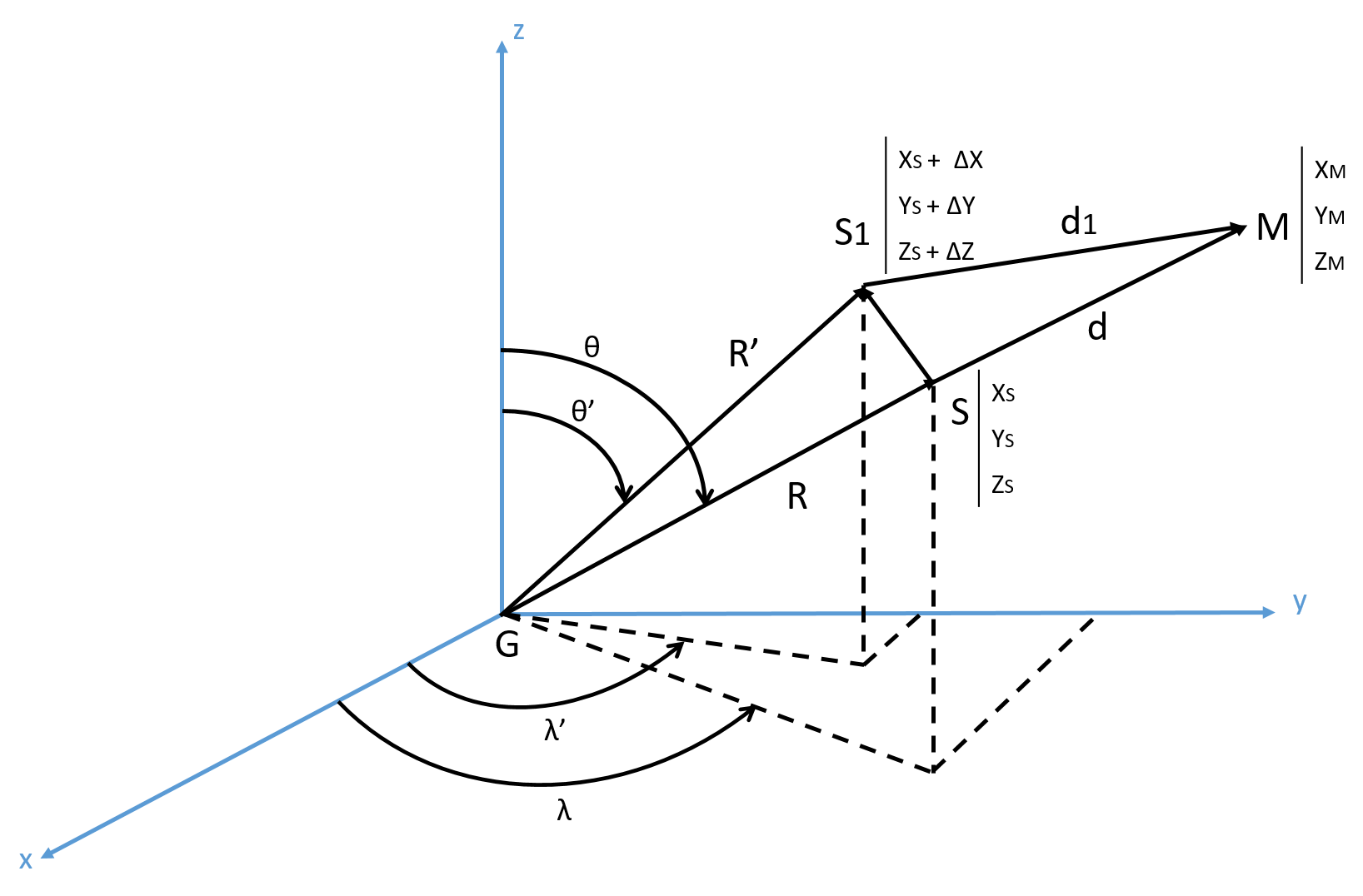
Ci-dessus une figure qui décrit la variation relative de la distance Terre-Lune dans le repère cartésien en fonction des coordonnées géodésiques de la station.
G : Centre de la Terre.
R : Rayon de la Terre.
R' : Rayon de la Terre + déplacement.
S : Un point à la surface de la Terre (on assimile la Lune à un objet ponctuel).
M : Position de la Lune.
d : Distance moyenne Terre-Lune partant d’un point à la surface de la Terre.
S1 : Nouvelle position du point apres un déplacement ds.
d1 : Nouvelle distance Terre-Lune.
SS1 : Déplacement ds.
Co-latitude de S : θ : Angle que fait S dans le plan (zGy).
Longitude de S : λ : Angle que fait la projection de S dans le plan (xGy).
Co-latitude de S' : θ'.
Longitude de S' : λ'.
Le but est d'estimer d2, la valeur relative de la distance Terre-Lune, donc le déplacement (horizontal et vertical sommés) de la station sur Terre : d2 = d1 - d.
Résultats
Voyons à présent l’impact qu’a l’effet combiné de ces charges sur le déplacement de la station. Graphiquement, la variation de la distance Terre-Lune au niveau de la station de Calern sur 1 an :
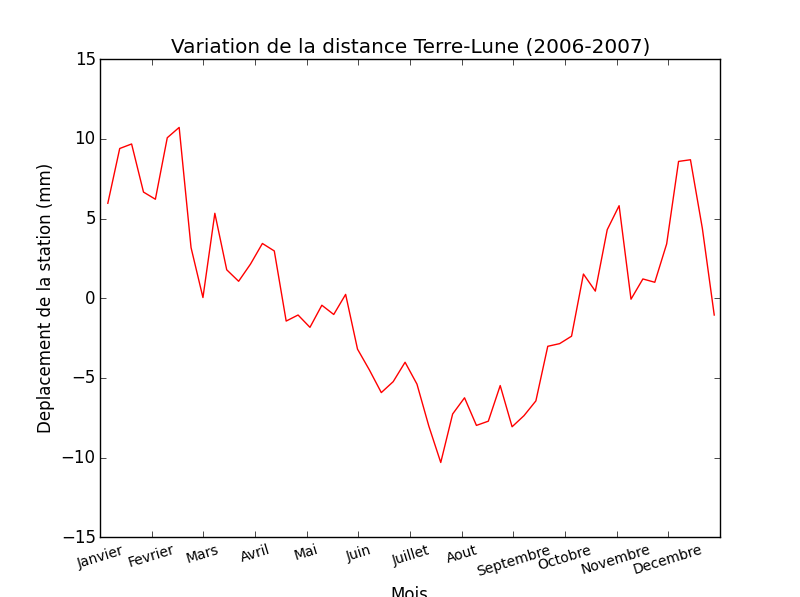
Conclusion
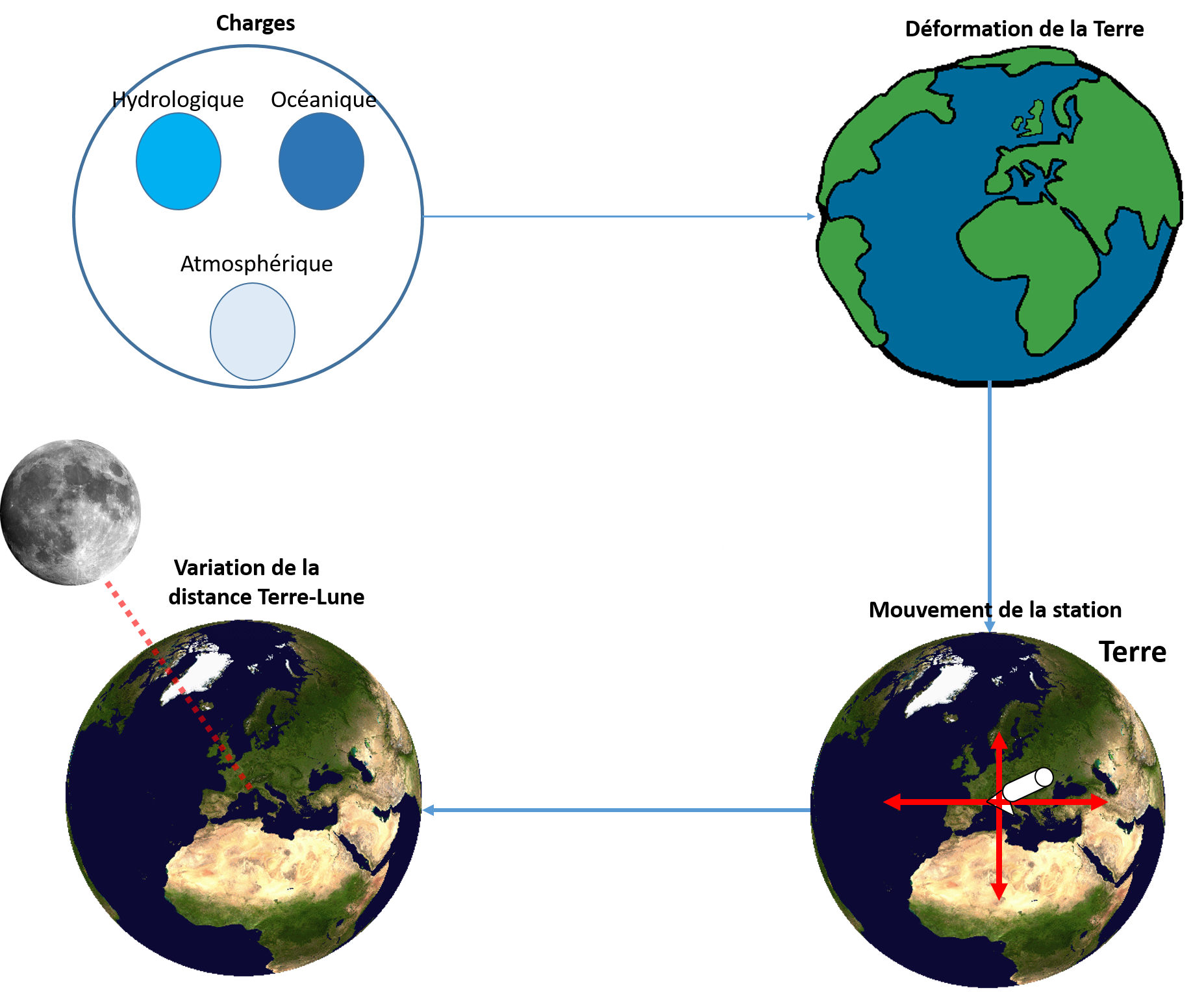
Nous avons vu que les variations de la distance Terre-Lune sont dues aux facteurs géophysiques qui engendrent des déplacements verticaux et horizontaux de la station de Télémétrie Laser de Calern. Pour étudier ces variations, nous avons créé des programmes informatiques en Python, permettant d’une part de quantifier les déplacement verticaux et horizontaux, d’autre part d’estimer avec plus de précision la variation de la distance Terre-Lune. Cependant, nous n'avons pris en compte qu'un seul facteur, le phénomène de surcharge et seulement trois effets de charges differentes. Cela nous a permis de voir que le déplacement vertical de la station de l'ordre de la dizaine de millimètres joue un rôle majeur dans les variations de la distance Terre-Lune et que la charge hydrologique est prédominante suivant la verticale. On peut ainsi conclure que le déplacement de la station impacte les variations de la distance Terre-Lune. Il est également possible de prédire la variation de la distance Terre-Lune à partir d'une autre technique de positionnement géodésique, le GPS. Nous pourrons comparer des données GPS aux données prédites par la Nasa.