Montage

Nous allons essayer de recréer une vague de tsunami. Mais pour pouvoir suivre la propagation de la vague et ainsi vérifier si cette vague a le même comportement qu’un tsunami réel, il faut que le bassin soit transparent. Pour reproduire des conditions réelles, le bassin doit faire une certaine longueur pour représenter le fait que le point d’origine se trouve à plusieurs centaines de kilomètres. En établissant dans notre laboratoire une échelle de 1/100000, c'est a dire qu'un centimètre représentera un kilomètre, nous utiliserons un bassin en plexiglas de 248,5 cm de long. Pour une raison de simplicité, le bassin sera rectangulaire avec une largeur de 22 cm. Mais cela est sans une grande importance, car la vague se propage circulairement autour du point d’impact et la largeur peut donc prendre n’importe quelle valeur. Mais pour nos calculs il sera plus simple de prendre une largeur pas trop grande pour pouvoir mieux suivre et calculer la vague et ses données.
Ensuite il faut modéliser la pente de la côte. Pour cela nous utiliserons un rectangle en plexiglas de la même largeur. Pour toutes les simulations que nous allons faire la pente sera toujours 22°.
Mais comment simuler le déclanchement de la vague par un tremblement de terre, un volcan sous-marin, un effondrement sous-marin ou une météorite ? Nous avons remarqué que ces quatre causes peuvent être regroupées en deux catégories correspondant à un déplacement de volume dû à:

1. Un mouvement sous-marin comme le tremblement de terre, le volcan ou l’effondrement,
2. Un ajout externe comme dans le cas d’une météorite.

Pour simuler une météorite, nous utilisons un ballon rempli d’eau lâché au-dessus de la surface d’eau du bassin. Comme l’eau à l’intérieur du ballon à la même densité que l’eau du bassin, le ballon va repousser l’eau du bassin.
Pour simuler les trois autres déclenchements, nous avons utilisé des objets flottants : un ballon rempli d’air et un flotteur en PE30. Nous les placerons sous l’eau et une fois la surface à nouveau calme, ils seront relâchés et remonteront à la surface déclenchant une vague.
Nous observerons alors la propagation de la vague tout le long du bassin, jusqu’à ce que la vague atteigne la pente simulant le rivage et établirons le comportement des variables longueur d’onde et l’amplitude.

Le bassin

Les sources

Déclanchement et propagation de la vague

Effet de la pente

la longueur d’onde à l’air de se tasser et l’amplitude d’augmenter.

Mesures

Méthode analytique

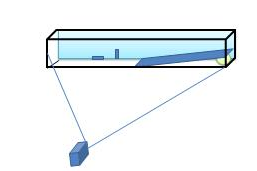La première méthode de mesure est une méthode analytique. Nous plaçons une caméra en face du bassin et nous filmons la propagation de la vague avec les trois différentes sources. Ensuite nous recommençons cette manipulation en changeant la hauteur d’eau du bassin. Grâce à un programme de traitement de vidéo, nous pouvons traiter chaque image de la vidéo. Ainsi nous pouvons mesurer la longueur d’onde et l’amplitude de notre vague.
En utilisant des logiciels de traitement de vidéo comme PYmecavidéo, nous allons visualiser image par image le vidéo, en suivant la crête des deux premiers vagues déclenchés. En ajoutant un troisième point qui sera placé sur la surface de l’eau encore immobile, nous pouvons ainsi déduire la longueur d’onde (distance entre les deux crêtes)

et l’amplitude (hauteur de la crête), donc la différence entre le point de la vague et celui de la surface de référence.

En suivant la même crête à un instant t et un instant t+ δ t, il nous est possible de mesurer la vitesse de la propagation : la distance qui a été parcourue divisée par le temps que cela a pris.

Si vous voulez connaître les résultats obtenue pour cette méthode: Résultats

Méthode avec la corrélation

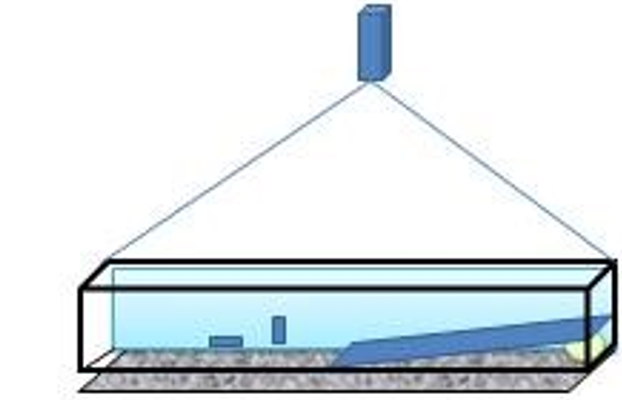La deuxième méthode utilise le principe de la corrélation et est basé sur la réfraction de la lumière qui se propage d’un milieu matériel à un autre, ici l’air et l’eau. Cela nous permet de mesurer la topographie d’une surface au cours du temps.

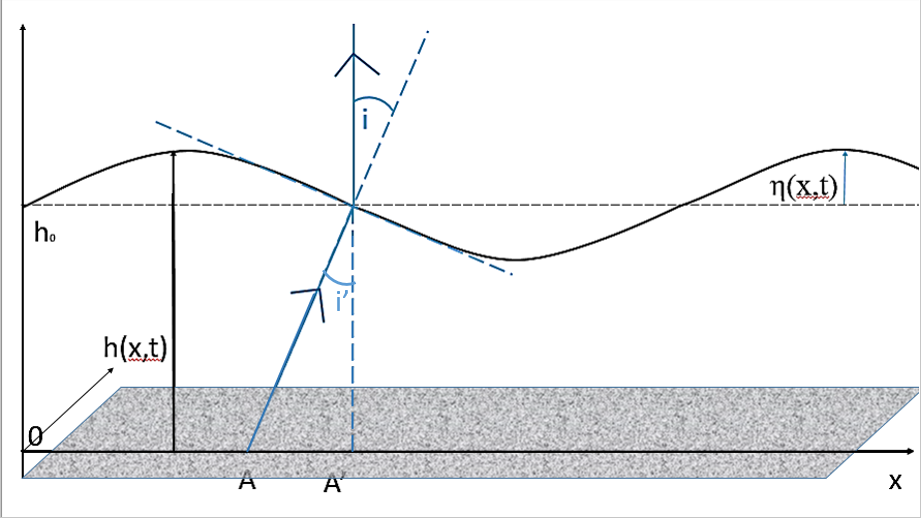Comment peut-on le comprendre ? Imaginons que l’on se trouve au bord de mer. En rentrant dans l’eau et si l’on regarde ses pieds, le sable ou les cailloux ont l’air de bouger. Mais pourquoi ? La cause est la réfraction : quand on regarde de haut, on pense que le point que l’on regarde se trouve droit en dessous. Mais ce n’est pas le cas ! La réfraction fait que le point se trouve perpendiculairement à la surface de l’eau. Quand la mer est calme il n’a donc pas de problème. Mais si la mer bouge, la surface change d’inclinaison en fonction de la vague. Donc le point qu’on regarde à l’air de bouger.
Pour notre simulation c’est exactement ce principe que nous appliquons. Seulement au lieu de mettre un objet dans l’eau qui pourrait fausser nos résultats, nous plaçons des feuilles imprimées de points aléatoires en dessous le bassin. Comme le bassin est transparent, on voit les points à travers de l’eau.
C’est maintenant que nous appliquons le principe de la corrélation: La corrélation est le procédé qui consiste à comparer deux images et en déduire le déplacement. Nous prenons donc une image de référence quand la surface de l’eau ne bouge pas et ensuite nous pouvons avec chaque image observer le déplacement du point de son origine.
En connaissant le déplacement maximal d’un point, nous connaissons l’inclinaison maximale de la vague et donc la hauteur maximale et ceci à chaque moment de l’expérience.