Analyse et Résultats

Méthode analytique

En visualisant les vidéos, nous constatons que l’effet de la pente sur la vague fait en sorte que la vague augmente pendant la simulation. Si la vague simulée a les même propriétés qu’un vrai tsunami, nous pouvons dire que notre simulation est un vrai petit tsunami avec le même comportement qu’aura la vague sur grande échelle.
Après d’avoir effectué les mesures et traité les images de la vidéo nous utilisons le logiciel Matlab pour travailler avec les coordonnées que nous avons obtenues lors de nous mesures.

  • La vitesse

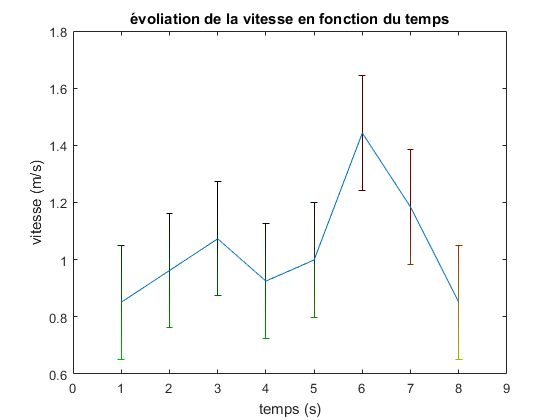    Evolution de la vitesse Nous constatons que la vitesse est restée constante pendant la première partie du bassin pendant la propagation. Avant de chuter, elle augmente légèrement, ce qui peut être négligé par rapport à une erreur de mesure. On peut donc supposer que la relation du tsunami, v=√ (g*h) est applicable sur notre modèle.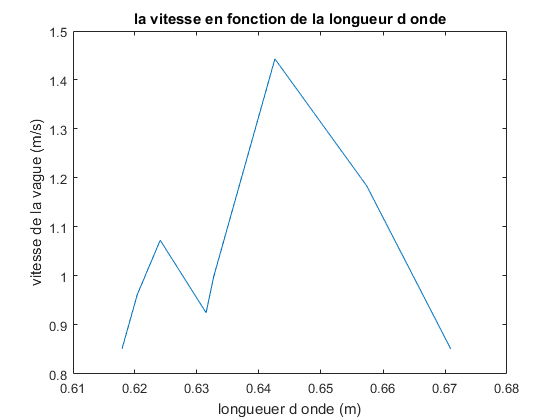

    La longueur d'onde en fonction de la vitesse Quand nous traçons la vitesse en fonction de la longueur d’onde, nous observons que la vitesse augmente jusqu’à une valeur de longueur d’onde de 64 cm et ensuite diminue à nouveau. Cela n’est pas logique car la vitesse est proportionnelle à la vitesse. On devrait donc avoir une droite.

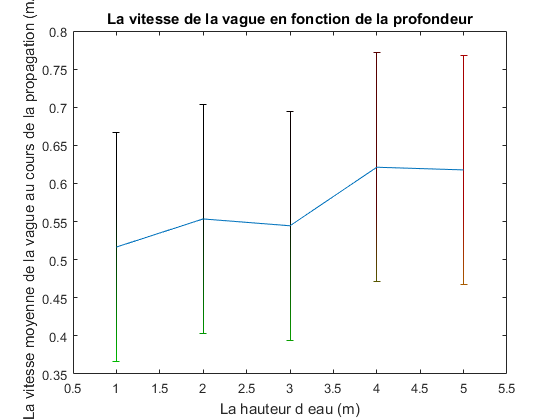    La longueur d'onde en fonction de la vitesse En traçant la moyenne des vitesses avant la pente en fonction des différentes hauteurs d’eau, nous observons que la vitesse se comporte de façon linéaire. Donc si la profondeur augmente, la vitesse également. Cela vérifie notre équation de Shallow Water qui dit que la vitesse dépend de la profondeur.

  • La longueur d'onde

    Evolution de la longueur d'onde 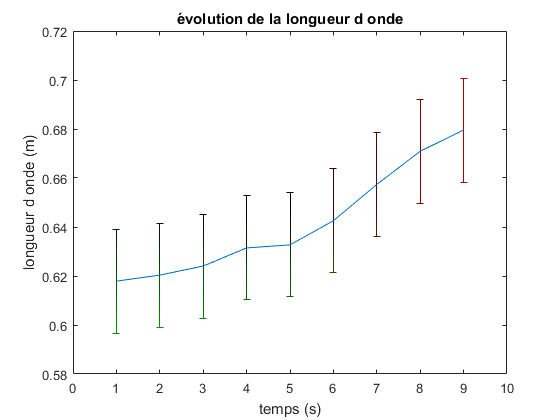Pour la longueur d’onde il faut également prendre en compte les barres d’erreurs. En faisant ainsi, nous ne pouvons pas etablir que la longueur d’onde de la vague reste constante tout le long de la propagation. En arrivant sur la pente, elle devrait diminuer. Cela n’est pas le cas et ne nous confirme donc pas que notre petit tsunami à le même comportement de sa longueur d’onde que le tsunami réel qui suit la formule : λ=T*√ (g*h)

  • L'amplitude

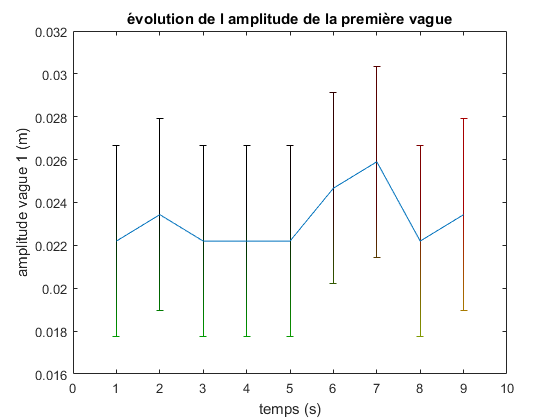    Evolution de l'amplitude En analysant le graphe de la longueur d’onde, nous constatons que l’amplitude ne change pas beaucoup au cours du temps. Mais le tsunami réel à une amplitude qui augmente !
    En ajoutant les barres d’erreurs, l’amplitude pourrait très bien augmenter au cours du temps arrivant sur la pente et jusqu’à ce moment-là, elle reste constante.

Méthode se basant sur la corrélation

Nous avons l’équation qui décrit le déplacement maximal du point: Equation Grâce à cette équation nous pouvons tracer les variables du tsunami en fonction d’autres variables :

  • La longueur d'onde

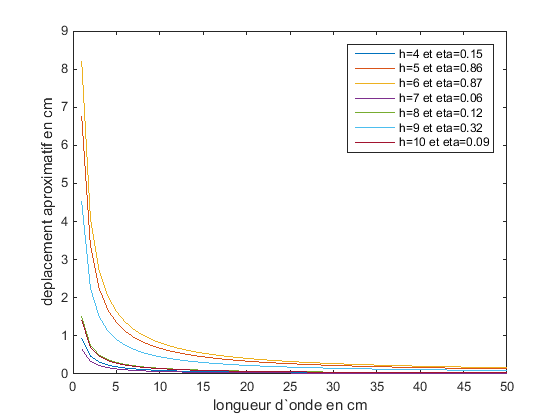    Déplacement en fonction de la hauteur d'eau Nous constatons que le déplacement diminue quand la longueur d’onde augmente, tombant vers 0. Donc quand la longueur d’onde est petite, le déplacement indique que l’inclinaison de la vague est très haute et donc la hauteur de la vague aussi. Sur le graphe nous voyons le comportement du déplacement du point avec différentes hauteurs d’eau. Ceci est logique car plus grande est la longueur d’onde, l’énergie doit se dissiper sur toute l’onde. Donc si la longueur d’onde est petite, l’énergie est plus concentrée dans le volume.

  • La hauteur d'eau

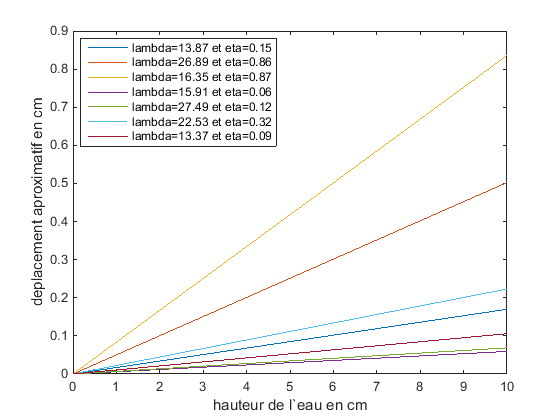    Déplacement en fonction de la hauteur d'eau Il est visible au premier coup d’œil que le déplacement d’eau change linéairement en fonction de la hauteur d’eau. Donc plus il y d’eau, et moins la longueur d’onde est grande, le plus le déplacement est important. D’une manière théorique ceci est logique: plus il y a d’eau, plus grand peut être le volume qui va de déplacer.