Analyse

Dans cette partie, nous analyserons plus rigoureusement le signal résultant du couplage dans l’espace de Fourier. Puis, on tracera les trajectoires obtenues dans l’espace de phase, espace construit par la méthode de « time delay embedding ». On tentera finalement d’étudier la divergence ou non de leurs trajectoires dans cet espace pour deux conditions initiales voisines.

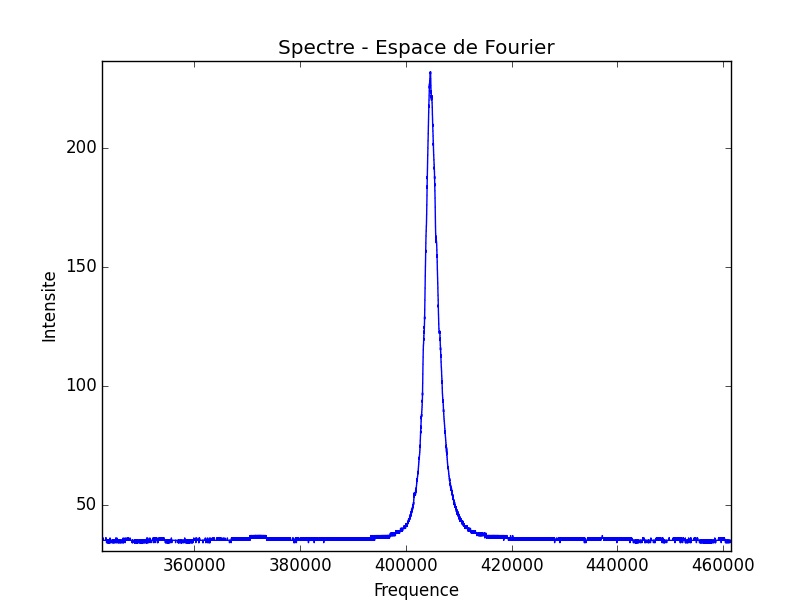
Tout d’abord, on se propose de comparer les spectres optiques dans les deux expériences.

Nous avons établi dans la première expérience deux pics correspondants aux fréquences d’oscillation de nos deux lasers.

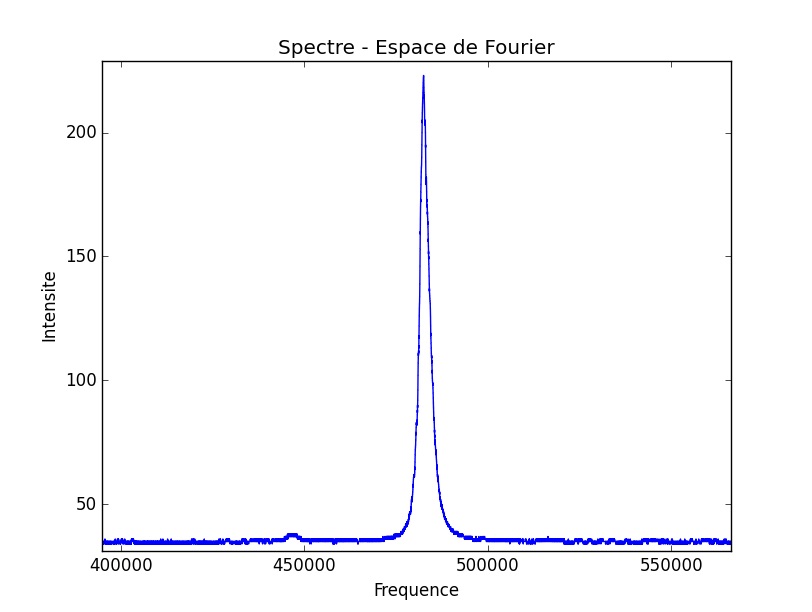
Lorsque nous augmentons le pompage, i.e, nous diminuons la fréquence d’oscillation du laser esclave, ce qui revient à déplacer le grand pic vers la gauche, nous relevons alors l’apparition d’un troisième pic que l’on apparie à un terme de corrélation non-linéaire.



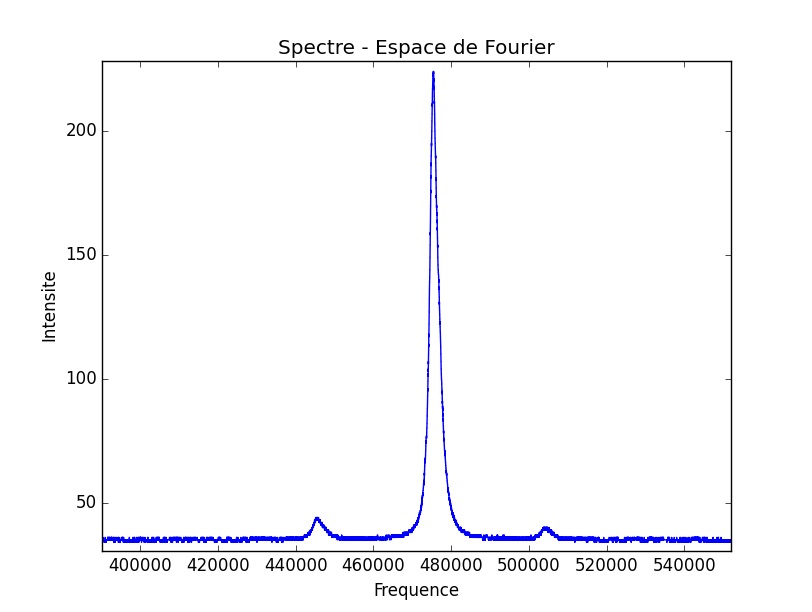
Puis, a lieu un phénomène très sensible et simple à relever expérimentalement car il dure pendant 4 acquisitions (soit une plage de 0.026mA) : un accrochage en terme de fréquences, visible lorsque les trois pics ne forment qu’un seul et unique pic. Cet accrochage rend compte d’un point fixe, d’un état stationnaire dans la dynamique de notre système.



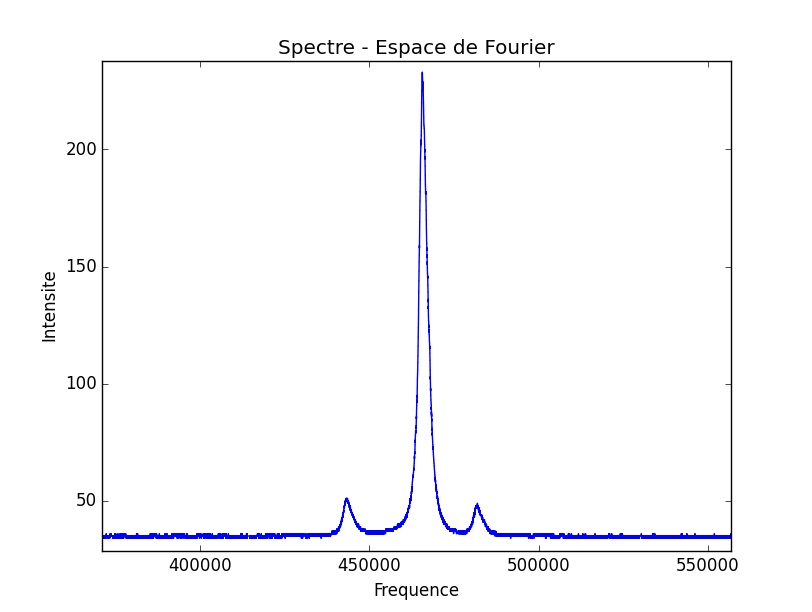
L’accrochage et le décrochage opérent bien de façon symétrique.



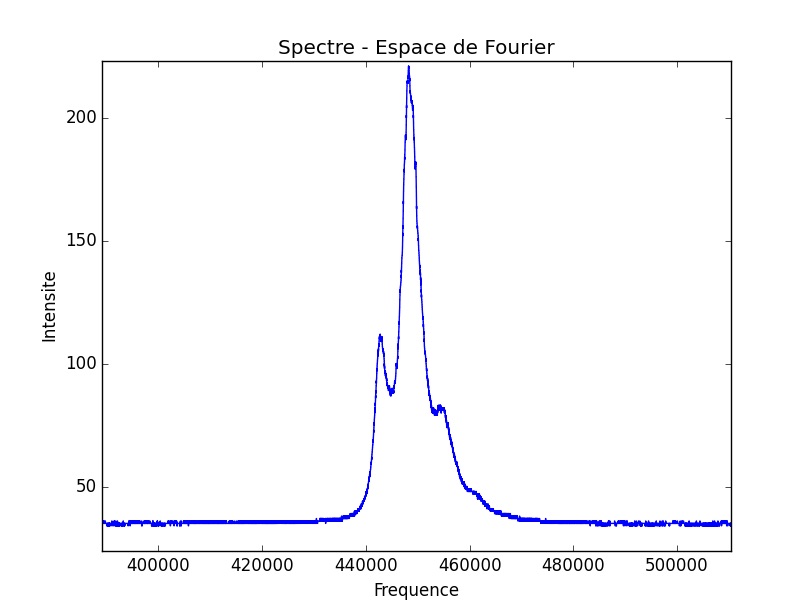
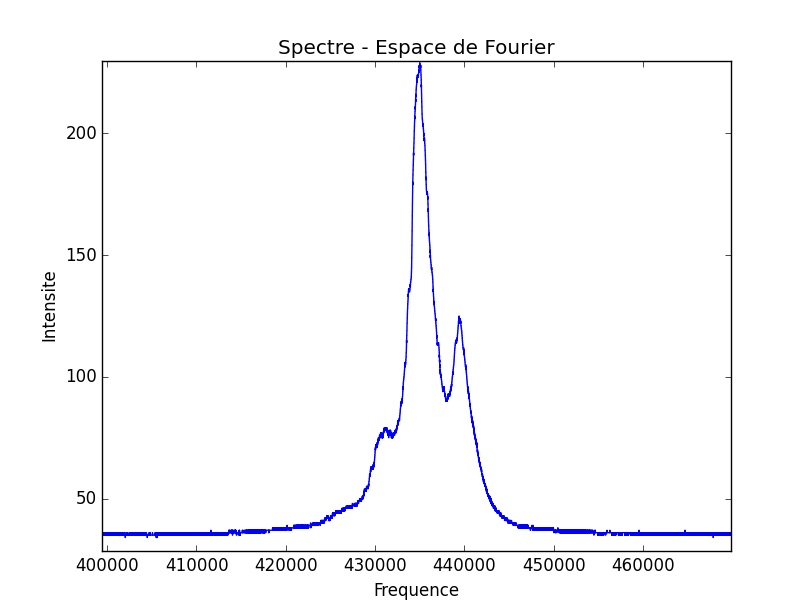
La décorrélation se produit de la même manière que la corrélation.



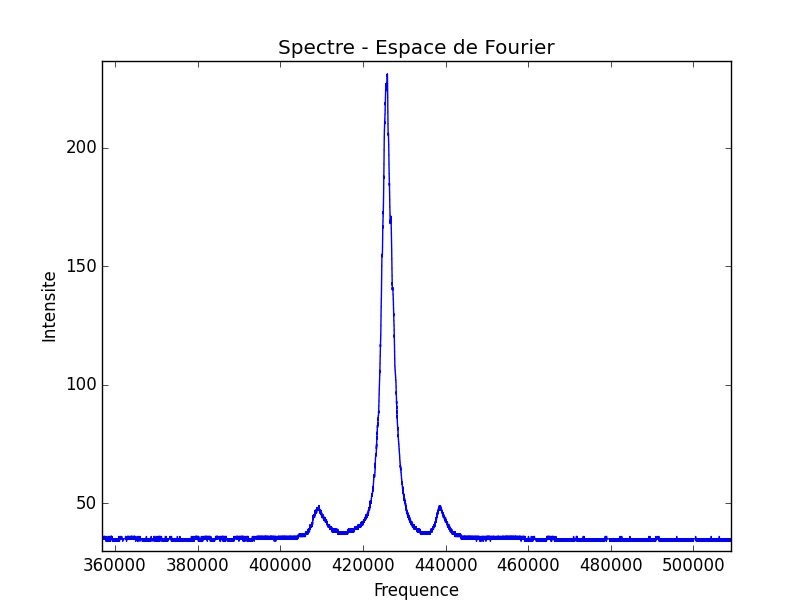
Étudions désormais les spectres optiques obtenus dans l’expérience 2.

Nous partons de la même situation que dans l’expérience 1 mais avec une amplitude de forçage du laser maître maximale. On y voit alors un pic associé d’amplitude plus élevée.



Nous observons un premier mélange (pompage électrique + champ injecté) à quatre pics apparaissant dans la cavité active du laser esclave, ce qui témoigne d’un processus hautement non linéaire, changeant entièrement la nature du mécanisme de détection. Ce spectre caractéristique manifeste du forçage délivré par le laser maître.



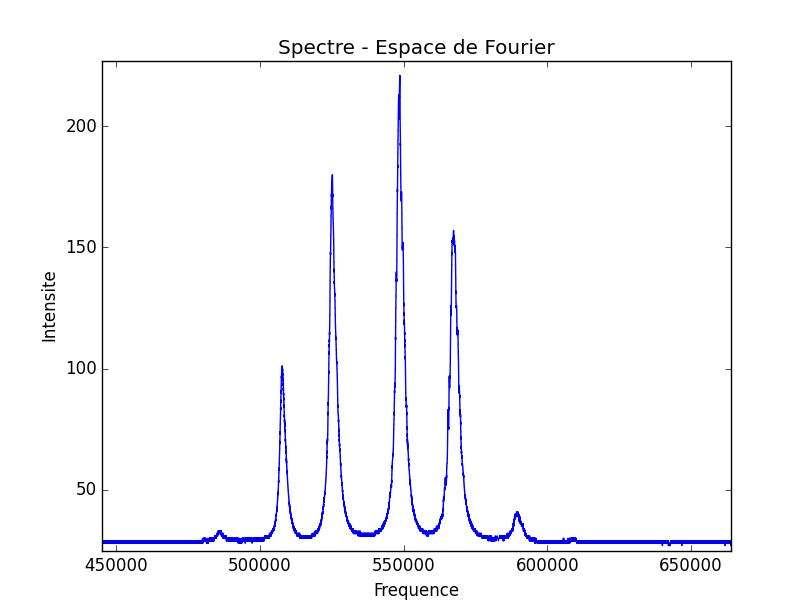
L’existence de spectres larges est une des caractéristiques des mouvements chaotiques d’un système. Toutefois, il est possible qu’en plus des raies larges, un système chaotique présente aussi des raies étroites semblables à celles d’un système régulier. [2] En d’autre termes, un spectre continu est une des caractéristiques d’un régime chaotique. Nous allons alors étudier plus tardivement dans l’espace de phase les trajectoires correspondant au spectre suivant pour identifier ou non du chaos et ainsi parvenir à une définition complète du chaos :



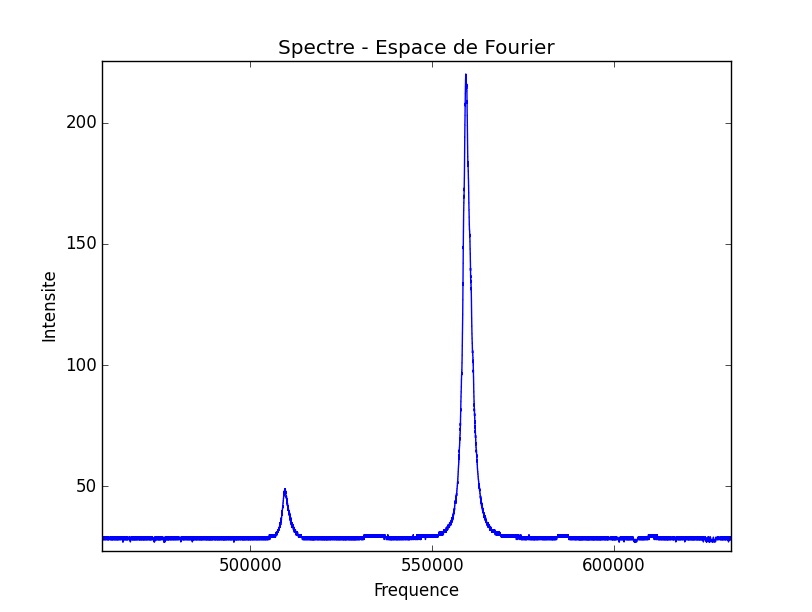
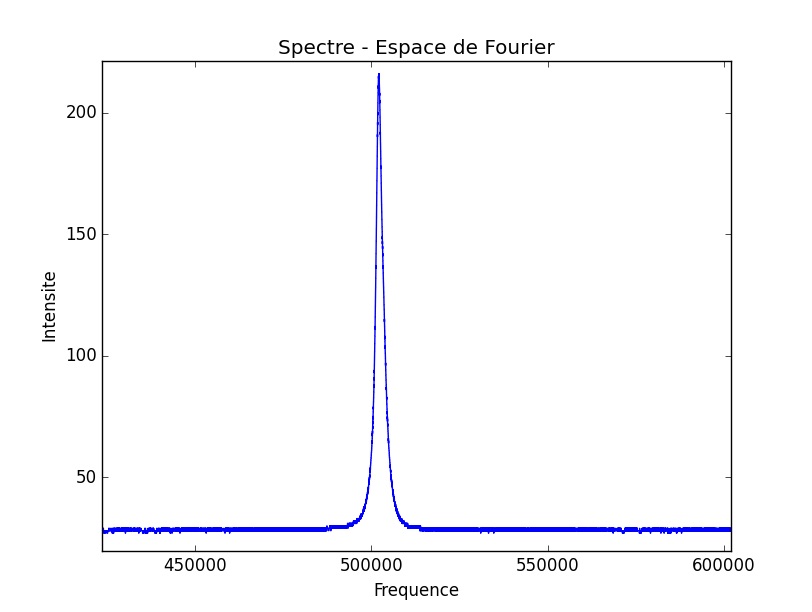
On assiste ensuite au phénomène d’accrochage en terme de fréquences comme dans l’expérience 1 et de même intervalle.



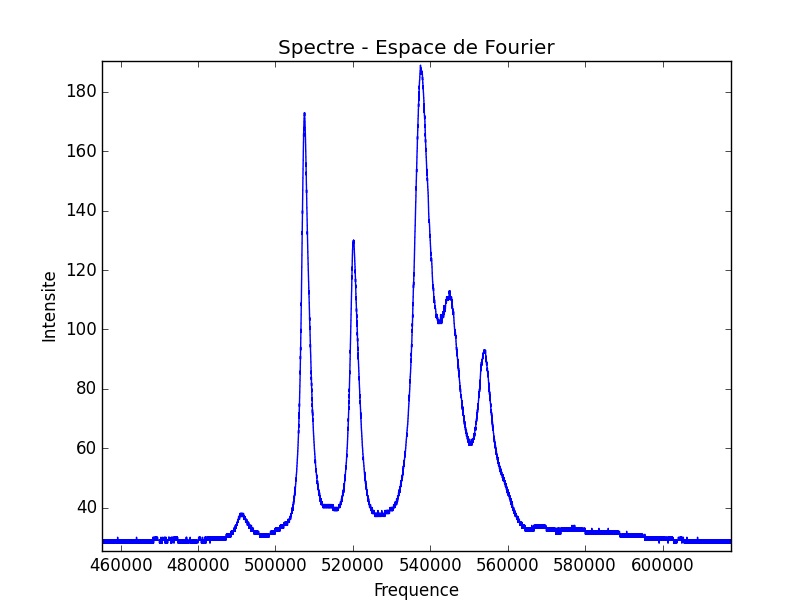
Après décrochage, on remarque l’apparition d’un mélange à 4 ondes comme précédemment, puis on relève des pics subjacents et intermédiaires aux pics établis et d’amplitude croissante. C’est ce que l’on appelle un doublement de période : l’un des scénarios les plus connus menant au régime chaotique.



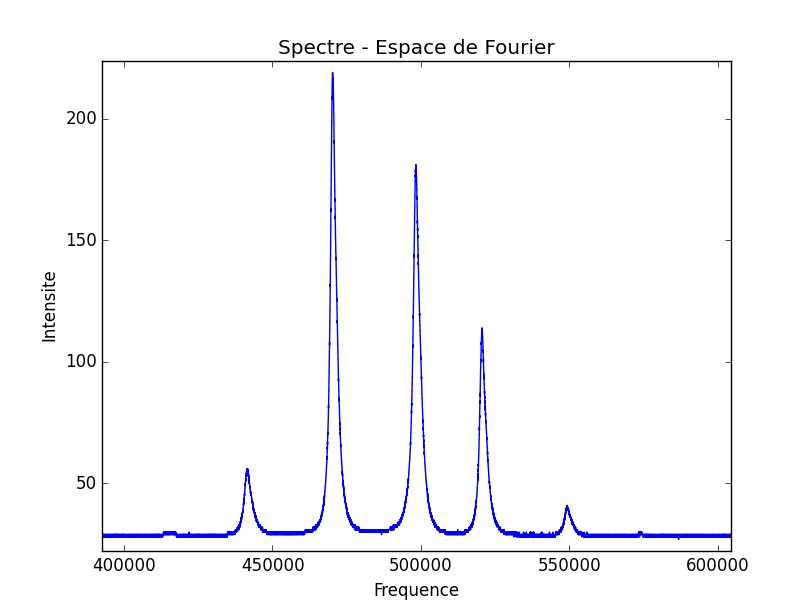
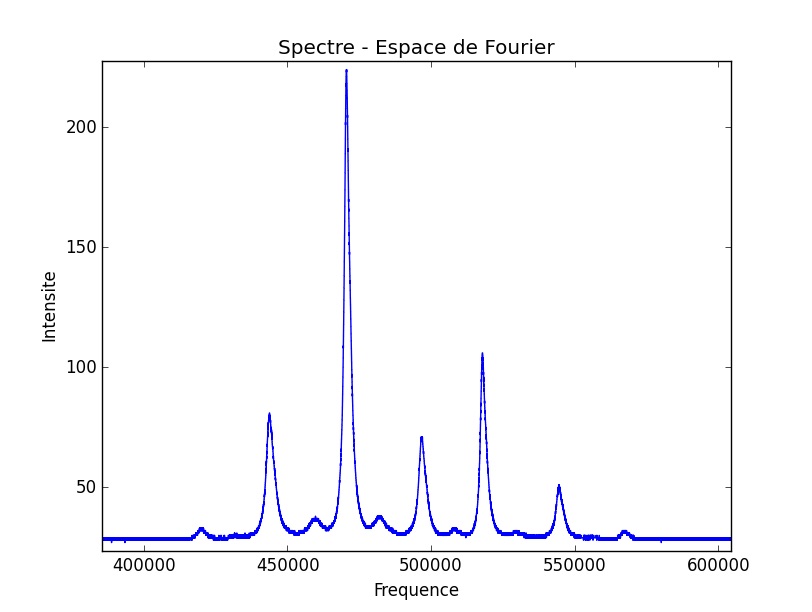
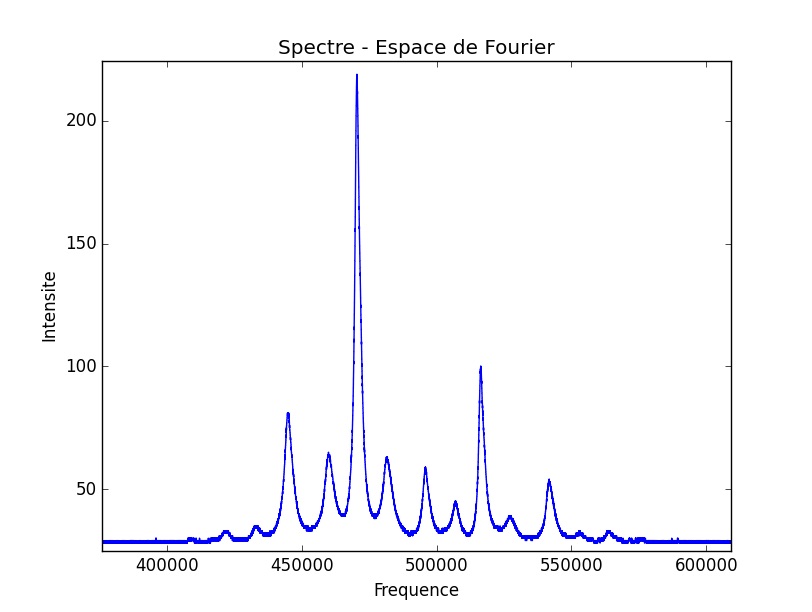
Nous observons enfin un spectre présentant une continuité relativement importante entre les pics, un socle large et irrégulier. Ce spectre témoigne d’un signal résultant dans l’espace réel particulièrement intéressant à étudier.



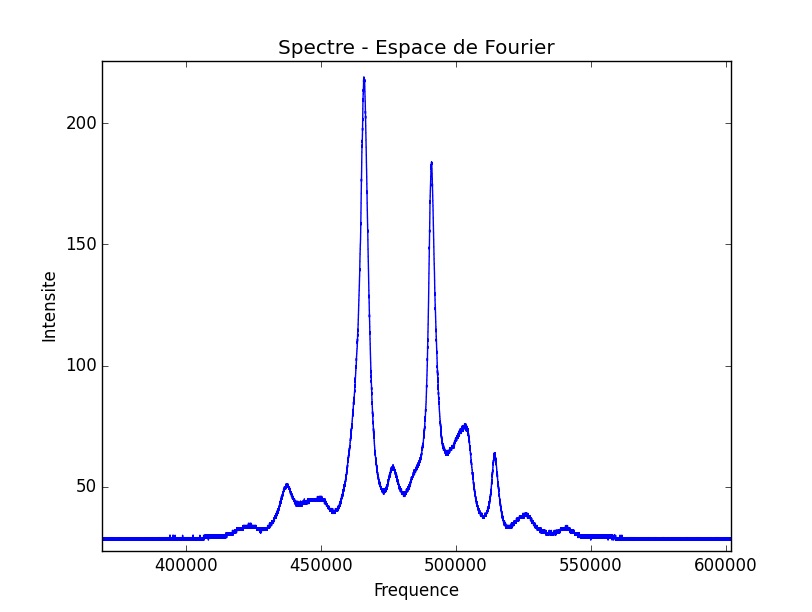
Finalement, on observe une décorrélation du spectre en deux pics s’éloignant l’un de l’autre, comme dans l’expérience 1.



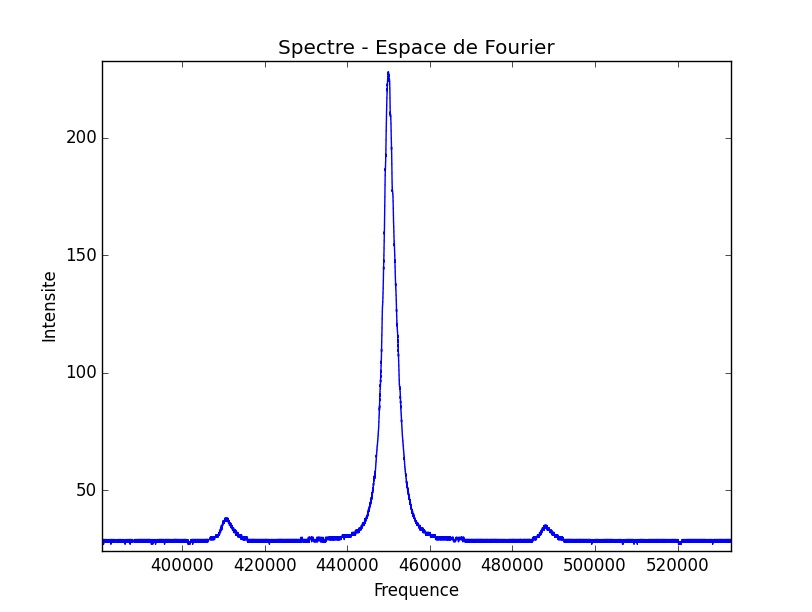
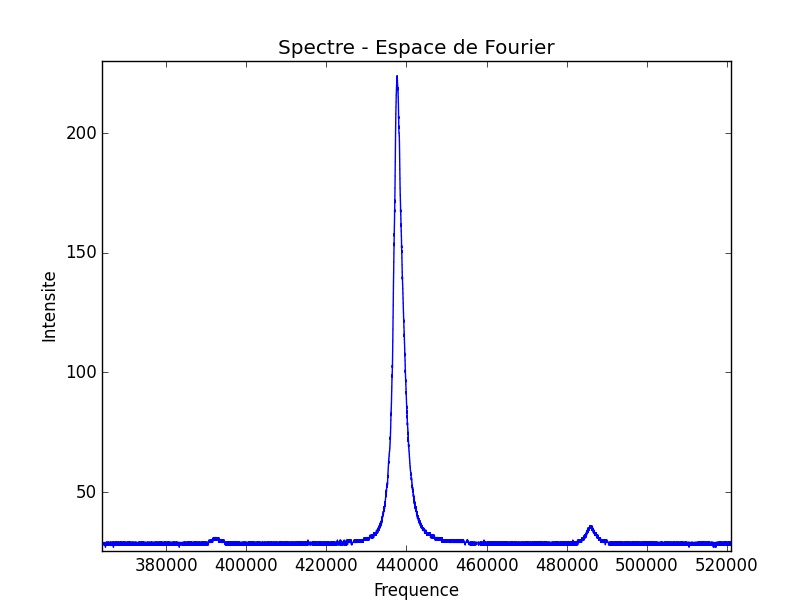
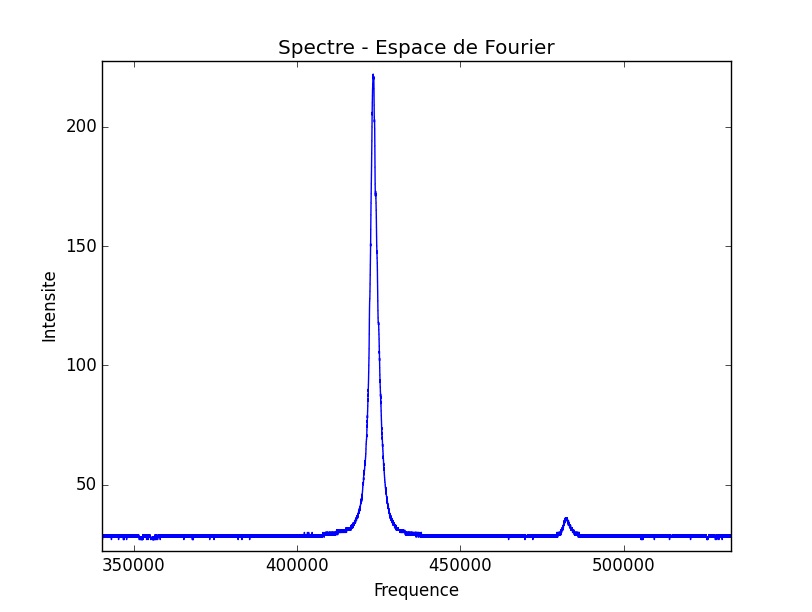
Une façon différente de visualiser notre série de mesures est une vue du dessus de l’ensemble des spectres en fonction de l’intensité électrique fournie au laser esclave. Nous obtenons alors :



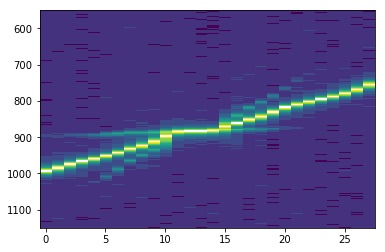
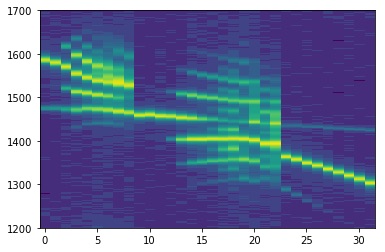
Nous observons explicitement dans la première photo tout d’abord les deux pics de nos lasers. Lorsque la corrélation a lieu, on distingue l’apparition du 3ème pic, puis l’accrochage, et enfin le décrochage qui s’effectue de façon symétrique. La deuxième photo présente des scénarios plus complexes : un premier régime hautement non-linéaire, un accrochage en terme de fréquences, puis un dédoublement de périodes explicite, i.e l’apparition de pics intermédiaires et équidistants aux pics existants, qui est une voie menant au chaos.

Passons désormais au comparatif des figures d’observations obtenues dans l’espace de phase reconstitué par la méthode de time delay embedding. (TDE)

Dans le chaos, la trajectoire n'est pas périodique. [7] La méthode de TDE, utile pour témoigner la présence de cette propriété, consiste à reconstruire un espace de phases en deux ou trois dimensions à partir d’une seule variable temporelle. On détermine alors une matrice dont chaque colonne détient la variable temporelle mesurée, mais en retard l’une par rapport aux autres. Chaque colonne constituera un axe. Ce retard est judicieusement choisi afin d’obtenir des figures d’observations optimales et lisibles dans l’espace de phases reconstitué.[5]

Nous allons introduire les figures que nous allons percevoir par un peu de théorie.

A chaque instant, l’état du système est défini sans ambiguïté par un point dans l’espace de phases. La cinétique du système est décrite par une trajectoire, une courbe dans cet espace. Lorsque le système évolue vers un état final d’équilibre, représenté par un point particulier de l’espace de phases, la trajectoire s’enroule autour de ce point. Le point d’équilibre étant le même pour toutes les trajectoires issues de points de départ pas trop éloignés, ce point constitue un attracteur. Il peut cependant y avoir plusieurs attracteurs, et l’ensemble des points de départ aboutissant à chaque attracteur constitue un bassin d’attraction.

Les trajectoires peuvent d’autre part s’enrouler autour d’autre chose qu’un point, par exemple une courbe ou une surface fermée (cercle ou ellipse dans les cas les plus simples, ou un tore ou hyper-tore s’il y a plus de deux variables). On a alors un attracteur cyclique, ce qui signifie que, quel que soit le point de départ situé dans le bassin d’attraction, la trajectoire finit par rejoindre une figure fermée dite cycle limite, correspondant à l’existence d’une solution oscillante. Cette figure est parcourue indéfiniment lorsqu’elle est atteinte. Les coordonnées sont alors périodiques.

Enfin, on peut observer des attracteurs chaotiques ou étranges. En effet, le chaos se caractérise aussi en étudiant les propriétés géométriques de l’attracteur étrange lui-même. La plupart du temps, il s’agit d’un objet fractal possédant une dimension non entière appelée dimension fractale, c’est à dire un objet composé de sous-figures structurées qui s’emboîtent. Les frontières entre ces différentes parties constituent des « des lignes fractales » ou de catastrophes. Le franchissement d’une des lignes fait basculer la dynamique du système d’un état d’équilibre local à un autre. L’attracteur chaotique peut être visualisé comme un seul fil tordu dans un nombre infini de boucles entrelacées. Il présente des caractéristiques frappantes telles que, par exemple, l'auto-similitude, c'est-à-dire la propriété d'exposer la même structure, dans un sens statistique. [7] On se servira de cette propriété pour étudier la sensibilité des trajectoires aux conditions initiales dans un système présentant une tel attracteur.

Nous proposons alors de comparer nos résultats obtenus des deux différentes expériences dans l’espace de phase, avec une amplitude de forçage plus faible (Exp.1) et une autre plus élevée (Exp.2), en utilisant la méthode TDE. Nous obtenons respectivement en 2D et 3D pour l’expérience 1 à gauche et 2 à droite :



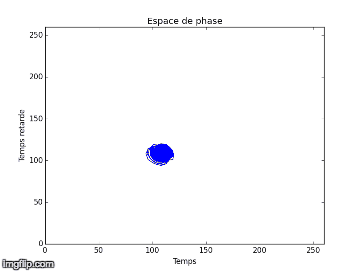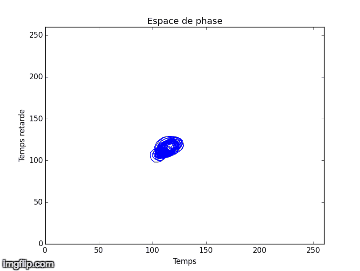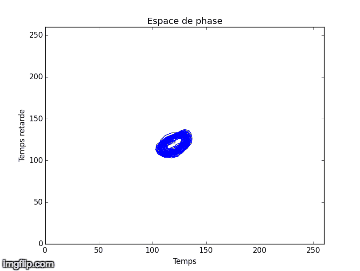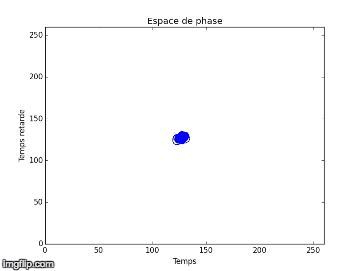
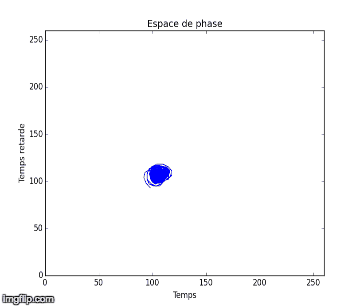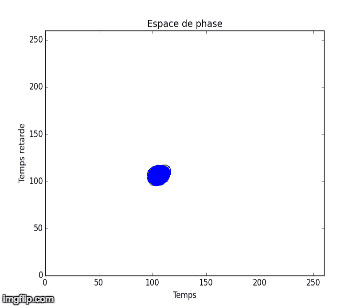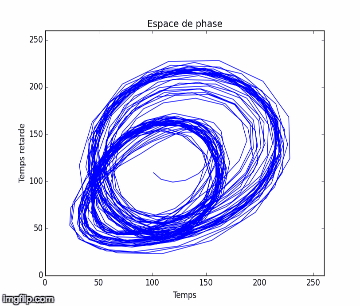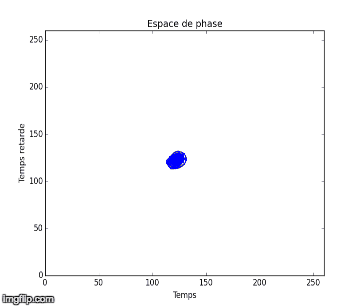
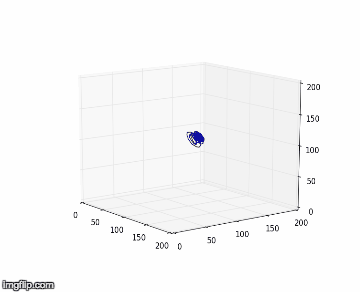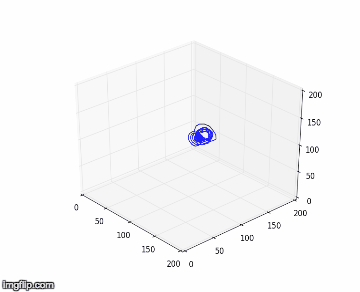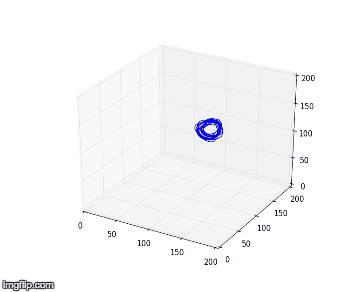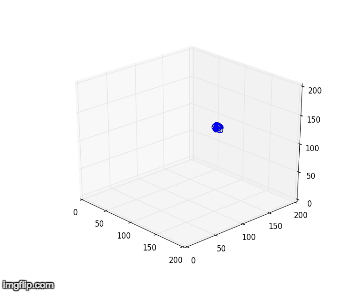
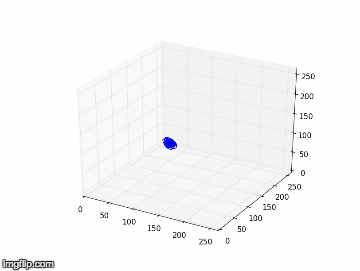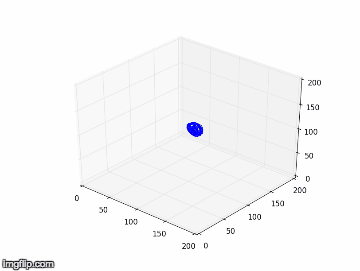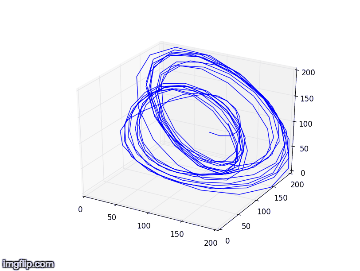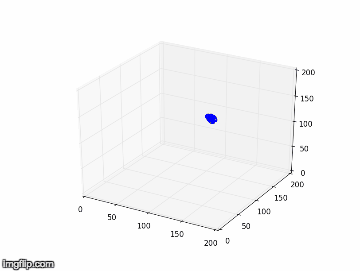
Nous notons que dans l’expérience 1, les figures obtenues sont soit un amas de points, soit un cycle plus ou moins régulier. Elles correspondent à des solutions stationnaires ou oscillantes. On a une transition d’un point fixe à une oscillation cohérente. Au vu de l’analyse spectral et des figures dans l’espace de phase, nous pouvons affirmer que du chaos n’est pas relevable expérimentalement dans l'expérience 1. On n’aperçoit pas d’attracteur étrange distinct, qui pourrait vérifier la sensibilité aux conditions initiales nécessaire à la détermination d’un régime chaotique.



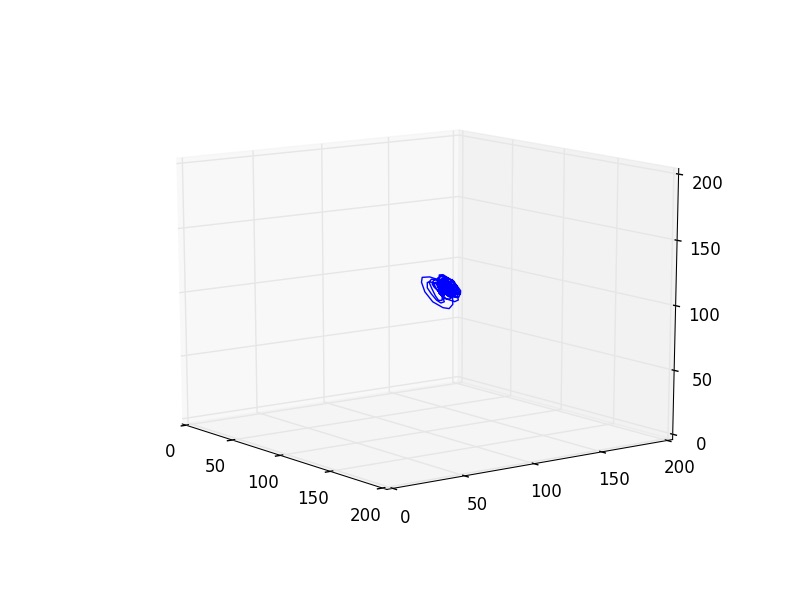
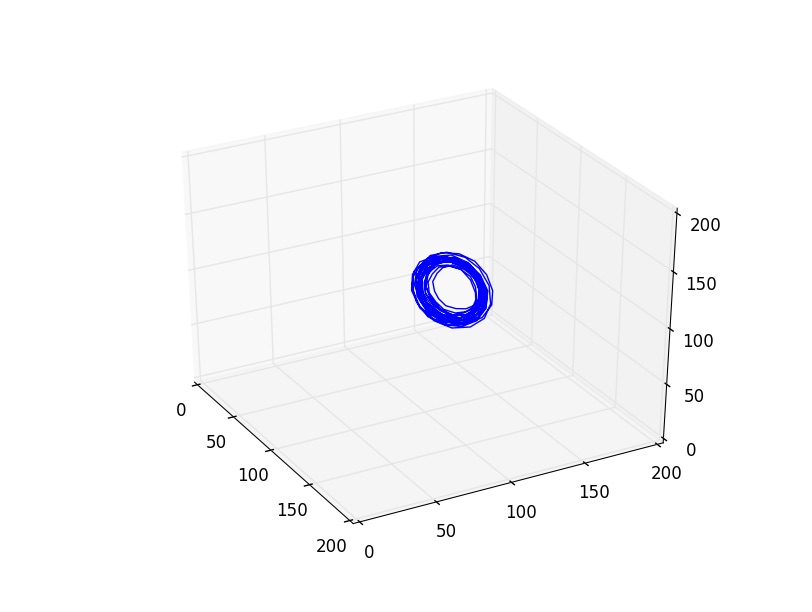
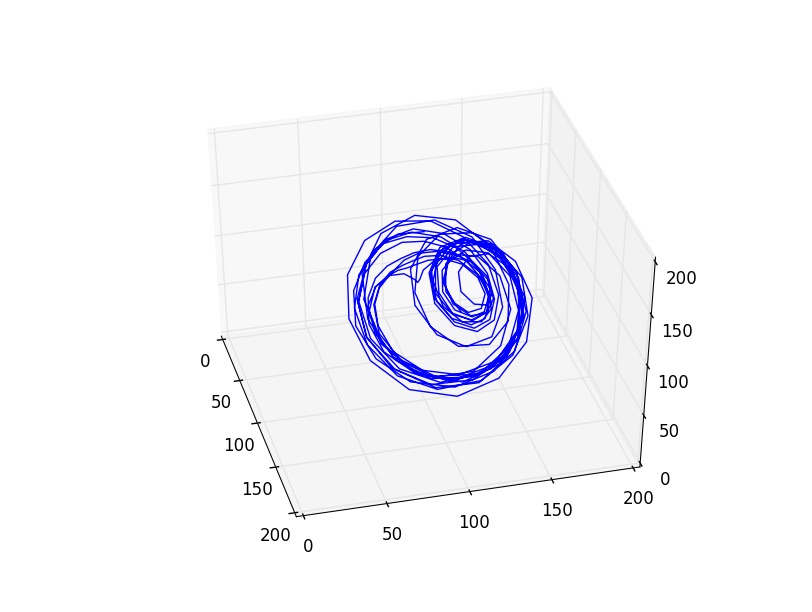
Nous remarquons que dans l’expérience 2, les figures obtenues sont plus complexes : amas de point, cycle régulier, cycle irrégulier et même attracteur étrange. Ces figures sont associés des situations dynamiques particulières : au mélange à 4 pics, on associe un cycle bien déterministe et régulier; au spectre continu et irrégulier, on y voit un attracteur parfois plus irrégulier, voir étrange, chaotique.



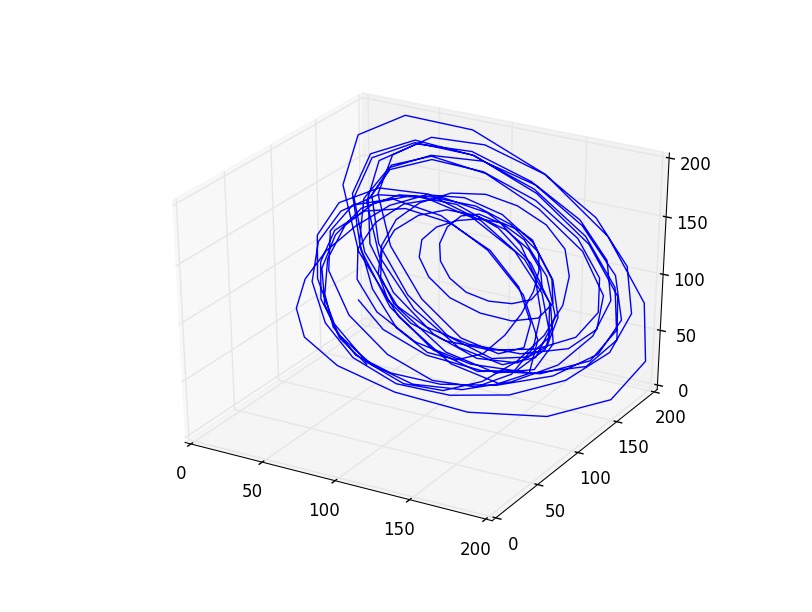
Nous parvenons alors à identifier la séquence de bifurcations menant au chaos correspondant à la voie de doublement de périodes. On peut la décrire comme une cascade de trois bifurcations : la première amène le système d'un point fixe à une orbite périodique, alors qu'après la deuxième bifurcation, l'attracteur devient un cycle limite car la deuxième fréquence générée est incompatible avec la première. Enfin, après la troisième bifurcation, on passe à un hypertorus. Ce dernier attracteur est habituellement instable et la dynamique devient chaotique. La première bifurcation correspond à trajectoire captée par un autre attracteur et l’on a simplement une transition d’un point fixe à un autre.



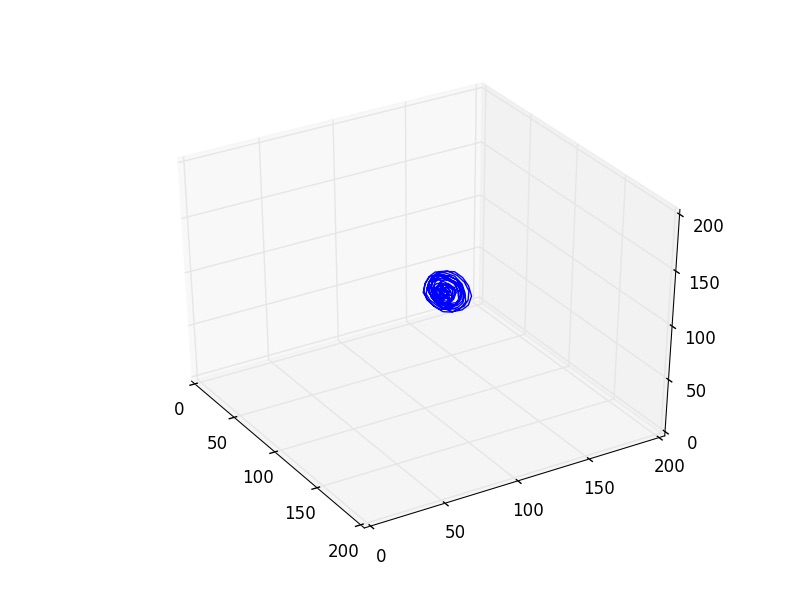
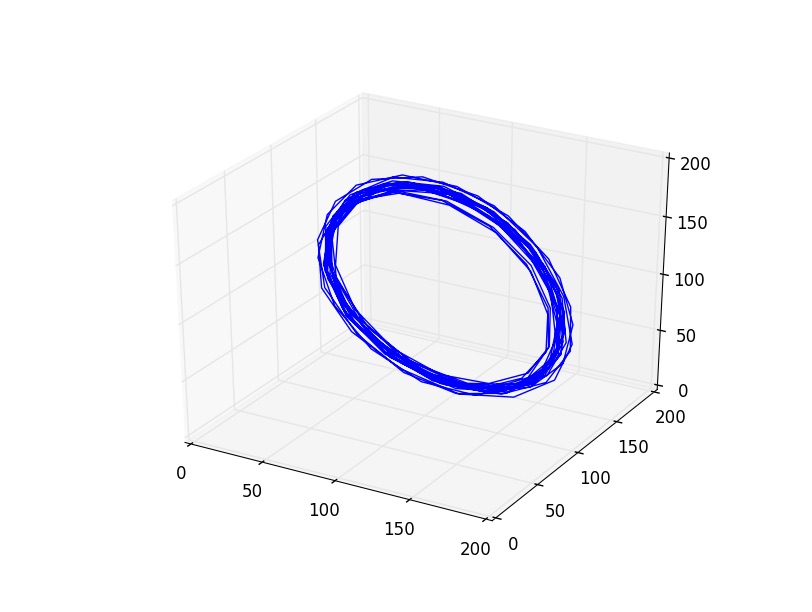
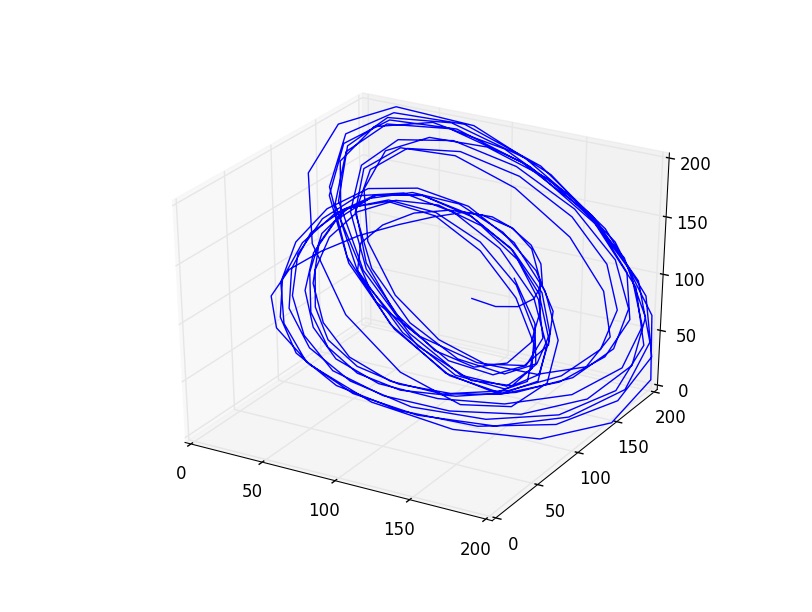
Lorsque le système présente des solutions chaotiques, les oscillations issues de deux conditions initiales voisines sont fortement corrélées au début de l’évolution, mais rapidement, la différence entre les deux trajectoires augment et conduit à une décorrélation totale après quelques oscillations. Cette fois-ci, la distance entre les deux trajectoires augmente exponentiellement avec le temps. La divergence exponentielle des trajectoires est due à l’impossibilité de connaître avec une précision infinie les coordonnées du seul point de départ. Le système manifeste alors une sensibilité extrême aux conditions initiales, déterminant ainsi un chaos déterministe.

Lorsque les attracteurs ne sont pas bien définis dans tout l’espace de phase, et ne sont donc pas exploitables, comme dans l’expérience 1, la divergence exponentielle des trajectoires n’est pas considérable. Cet argument nous a permis d’exclure la présence de chaos au sein de cette expérience. Toutefois, nous allons tenter de vérifier cette propriété dans l’expérience 2, avec une amplitude de forçage maximale.

Pour des trajectoires vérifiant la SCI, le système associé n’admet aucune prédiction précise, on ne prévoit qu’un comportement statistique et l’existence de basculements catastrophiques à des instants imprévisibles.[1] Cela constitue notre caractère principal pour évaluer la présence ou non de chaos.

Nous considérons alors pour un espace de phase donné, un amas de points correspondant à des conditions initiales voisines. Nous voulons voir comment ces points évoluent au cours du temps indépendamment des autres, chaque point suivant sa trajectoire dans l’espace de phases. Si la distance entre deux points n’augmente que très peu ou de façon linéaire, alors on n’exclut la présence de chaos dans un tel système. Si, au contraire, la distance entre chaque point augmente de façon exponentielle, alors on a vraisemblablement affaire à régime chaotique. Les points initialement très proches prendraient alors place dans l’ensemble de l’espace considéré.

Tout d’abord, regardons un cycle parfaitement régulier dans l’expérience 2 pour i=1.,172mA.



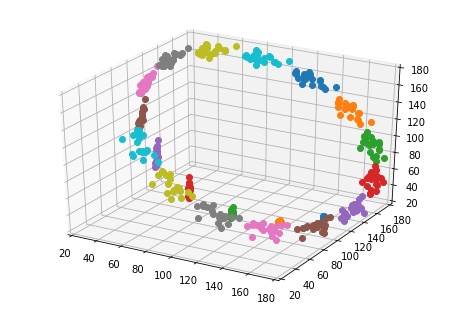
On y voit un système purement déterministe et les trajectoires restent nettement corrélées.

Puis, pour des intensités électriques suivant le mélange à quatre ondes relevé précédemment, nous obtenons l’’évolution suivante :



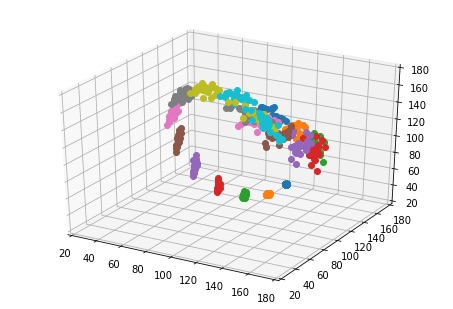
La distance relative entre les points n’évolue clairement pas de façon exponentielle. Quant bien même le signal obtenu présente des distinctions dans les deux espaces d’étude, nous arrivons à la conclusion que dans ce régime, le chaos ne règne pas.

Finalement, nous allons étudier le spectre avec un motif continu, suivant le doublement de périodes, correspondant à une voie menant au chaos.



Les points initialement proches vont s’étaler dans l’ensemble de l’espace de phases au bout de quelques pas seulement. On a bien affaire à une divergence exponentielle des trajectoires, manifestant une sensibilité extrême aux conditions initiales. Dans ces conditions règnent alors le chaos.

Remarque générale : Nous tenons à préciser qu’au cours des acquisitions, nous avons uniquement étudié la cascade de bifurcations menant au chaos de notre système en augmentant le pompage électrique, i.e, en diminuant sa fréquence d’oscillation. Lorsqu’on diminue le pompage, i.e, on augmente la fréquence d’oscillation, un scénario différent peut se manifester.