Méthode de Boltzmann sur réseau
Présentation
La méthode de Boltzmann sur réseau ou en anglais Lattice Boltzmann Method (LBM) est issue de la théorie cinétique des gaz établie par Boltzmann.
Cette méthode est très utilisée dans les domaines de dynamique des fluide.Elle permet de modéliser des phénomènes physiques à petite échelle avec une grande précision.
De plus comme nous l'avons expliqué dans l´introduction du projet, l'ordinateur ne pouvant pas traiter les données continues qu´admet l´équation de Boltzmann, cette méthode permet de la discrétiser en effectuant un maillage sur l´espace en deux dimensions.Plus cette discrétisation sera fine plus on se rapprochera du problème réel continu.
On considère un fluide se déplaçant de manière aléatoire dans cet espace constitué d´un grand nombre de particules. Les échanges d´énergie et de quantité de mouvement se font grâce à la diffusion et à la collision de particules qui interagissent telles des boules de billard au sein du fluide. Les chocs sont ellastiques et binaires, c´est à dire que les particules n´interagissent que deux à deux et qu´il n´y a pas de dissipation d´énergie lors de la collision.
L´équation de Boltzmann décrit un fluide par le biais de sa fonction de distribution. La résolution numérique de cette équation nécessite sa discrétisation par rapport à l´espace des positions et l´espace des vitesses.
On réalise une grille de noeuds espacés d'un pas Δx.On suit le schéma de la méthode DnQm, n étant la dimension du domaine et m le nombre de possibilités de directions de propagation du fluide. On se trouve donc dans notre cas en D2Q9 (2 dimensions et 9 possibilités de déplacement). Chaque chemin possible est associée à un vecteur vitesse \(\vec{e}_i\) défini par :
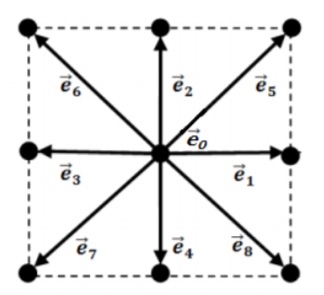
À chaque noeud sur le réseau correspond une fonction de distribution \(f_i\)(\(\vec{x}\),t) avec l´indice i=0,..,8 faisant référence aux vitesses discrètes et aux directions \(\vec{e}_i\) des particules. La fonction distribution est liée aux variables macroscopiques suivantes: la densité ρ(\(\vec{x}\),t) et la vitesse \(\vec{u}\)(\(\vec{x}\),t). Elle décrit la probabilité pour une particule de se diffuser dans une direction privilégiée.
Ces quantités sont définies par:
Diffusion
Collision
On s'intéresse ici à la partie gauche de l´équation de Boltzmann qui décrit l'étape de diffusion dans laquelle chaque distribution de particules de fluide se déplace vers les noeuds voisins du réseau selon la direction \(\vec{e}_i\) qui lui est associée.
Voici un schéma décrivant le processus de diffusion:
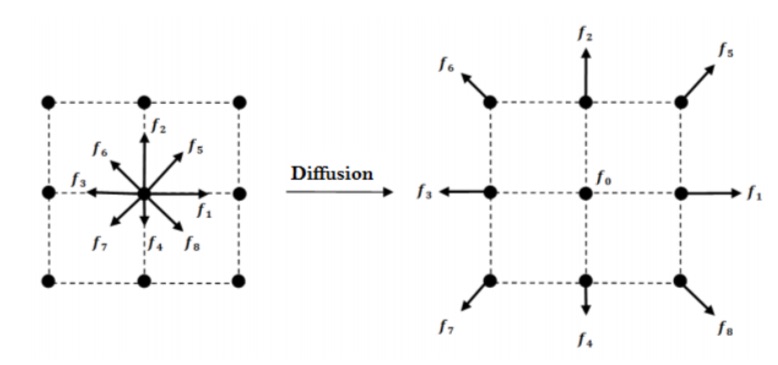
Aprés le processus de diffusion, à chaque point de l´espace est associé 9 nouvelles distributions de particules : \(f_i (\overrightarrow{x} + c\overrightarrow{e}_i,t + \Delta{t})\).
Dans notre programme nous choisissons des valeurs de c, Δx et Δt tels qu'elles répondent à la loi: $$c = \frac{\Delta{x}}{\Delta{t}}=1$$
Afin de simplifier le calcul on impose c=1.
À partir de cette nouvelle distribution, on va calculer les nouvelles valeurs des variables macroscopiques ρ et \(\vec{u}\) en utilisant les relations définies précédemment.
La partie droite de l´équation de Boltzmann décrit l´étape de collision, elle intervient après l´étape de diffusion, dans laquelle deux particules qui se trouvent au même noeud du réseau entrent en collision.
On simplifie cet opérateur en utilisant l´opérateur Bhatnagar–Gross–Krook, du nom de ses créateurs (BGK) qui se substitue à l´opérateur de collision de Boltzmann. Cette approximation va nous permettre de résoudre l´équation de Boltzmann plus facilement car le terme de relaxation vers l´équilibre est beaucoup plus simple que le véritable opérateur. Elle est néanmoins très bonne pour une interaction moléculaire qui respecte les propriétés fondamentales de conservation de la densité, de la quantité de mouvement et de l´énergie.
Voici l´opérateur BGK :
où \(f^{eq} (t,x,v)\) est la distribution d´équilibre locale.
La forme discrétisée de l´équation de Boltzmann se présente sous la forme :
La partie de droite est l´opérateur BGK discrétisé.
où \(f_i^{eq} (\overrightarrow{x},t)\) est la fonction de distribution à l´équilibre : \begin{eqnarray} f_i^{eq} (\overrightarrow{x},t) = w_i\rho[ 1 + 3\frac{\overrightarrow{e}_i.\overrightarrow{u}}{c} + \frac{9}{2}\frac{(\overrightarrow{e}_i.\overrightarrow{u})^2}{c^2} - \frac{3}{2}\frac{\overrightarrow{u}.\overrightarrow{u}}{c^2} ] \label{fequilibre} \end{eqnarray}
où c: la vitesse des particules sur la grille
\(w_i\): le poids qui correspond à la probabilité que la particule bouge suivant le lien i. Il prend les valeurs pour le modèle D2Q9 : $$w_i = \left\{ \begin{array}{ll} 4/9 & \mbox{i = 0}\\ 1/9 & \mbox{i = 1,2,3,4}\\ 1/36 & \mbox{i = 5,6,7,8} \end{array} \right.$$
On obtient donc grâce à cette formule une version discrète de la distribution de vitesse de Maxwell centrée autour d´une vitesse moyenne \(\vec{u}\). Durant cette étape on modifie la fonction de distribution et on recalcule sa valeur après un temps de relaxation τ en utilisant l´opérateur BGK discrétisé.
On donne aussi l´expression de la viscosité cinématique ν qui permet de remonter au temps de relaxation τ, qui caractérise le temps que met la fonction de distribution en terme de vitesse pour revenir à son état d´équilibre.\begin{eqnarray}
\nu = \frac{2\tau - 1}{6}\frac{(\Delta{x})^2}{\Delta{t}}
\end{eqnarray}
ν,c et Δx sont des paramètres du problème connus et définis précédemment.
On décidera par la suite de fixer la viscosité en prenant celle de l´air à 25°C \(ν=15,6.10^{-6} m^2.s^{-1}\).C´est donc le temps de relaxation τ qu´on cherchera à calculer dans notre programme.
Modélisation
Schéma algorithmique
- Initialisation de ρ, \(\vec{u}\),\(f_i\),\(f_i^{eq}\),
- Étape de diffusion : déplacement de la particule vers le noeud voisin suivant la direction \(\vec{e_i}\) ;\(f_{i} \rightarrow f_i^{\ast}\)
- Calcul des nouvelles valeurs des variables macroscopiques ρ et \(\vec{u}\)
- Calcul de la fonction de distribution à l´équilibre \(f_i^{eq}\)
- Étape de colision : actualisation de la valeur de la fonction de distribution \(f_i = f_i^\ast - \frac{1}{\tau}(f_i^\ast - f_i^{eq})\)
- Retour à l´étape 2
Conditions aux bords
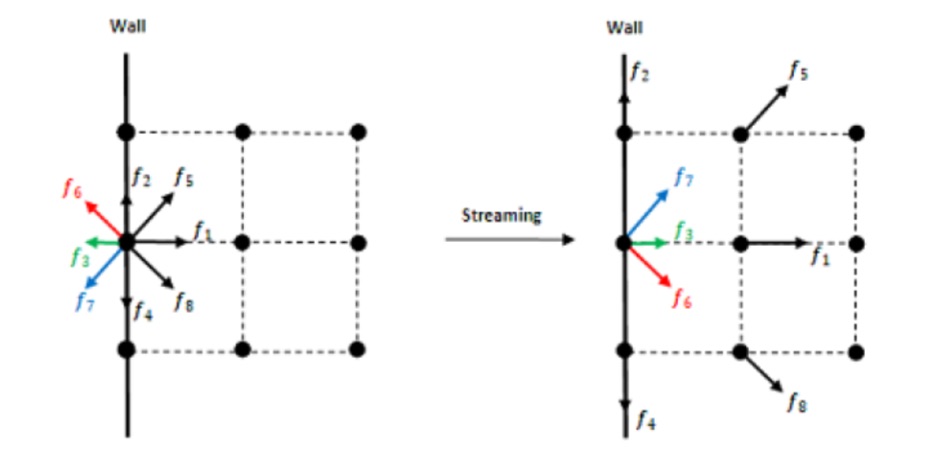
- La distribution de particules \(f_i\) se déplace dans la direction \(\vec{e_i}\) vers la case suivante sans rencontrer d´obstacle.
- La distribution se déplace vers la case suivante qui est un obstacle et est donc renvoyée dans la direction opposée.
- La distribution est déjà sur une paroi et se déplace de manière tangentielle à cette dernière, elle "glisse" sur la paroi.
Voici l´algorithme utilisé pour l´exécution de notre programme:
L´opérateur BGK peut définir la réaction des particules lorsqu´elles rentrent en collision entre elles mais pas lorsqu´elles le font avec un obstacle ou un mur. Il est donc nécessaire de mettre en place des conditions aux bords pour prévoir leurs comportements dans ces cas là.
Lors des premiers essais du fonctionnement du programme, nous n´avons pas établi de réelles conditions aux bords mais une simple périodisation des limites. À la fin de l´espace une particule va se retrouver de l´autre côté, ceci est peu physique mais permet de tester la fonction de diffusion dans toutes les directions de notre espace à deux dimensions. On attribue une quantité non nulle pour seule distribution dans une case de l´espace. On fait tourner la fonction pendant plusieurs pas de temps et on remarque que la distribution se propage correctement.
On peut donc desormais mettre en place les premières réelles conditions aux bords. On impose des murs autour de notre espace, ce qui limitera la propagation du fluide.Le but étant que lorsqu´une particule entre en contact avec l´un des murs, elle rebondisse dans le sens opposé. On a donc modifié notre fonction de distribution pour qu´elle est un comportement adéquat face à ces obstacles.
Après un pas de temps on distingue 3 cas possibles :
Vers une compréhension physique des phénomènes
Dimensions des paramètres
- Une unité de longueur : \(l_x\) \((m)\)
- Une unité de vitesse : \(c\) \((m.s^{-1})\)
- Une unité de temps : \(\frac{l_x}{c}\) \((s)\)
- Une unité de vitesse du son physique : \(c_{s,p}=c*c_s={c\over √3}\) \((m.s^{-1})\)
Utilisation du profil de Poiseuille
Le but étant de pouvoir interpréter les résultats obtenus suite à notre simulation numérique. On cherche à donner des dimensions physiques à nos variables.
Pour cela on utilise la méthode de conversion des unités du réseau de Boltzmann en unités physiques.
On définit :
\(c_s\) est la vitesse du son fixée pour la méthode BGK à \(c_s={1\over √3}\) .
De cela on peut tirer la valeur de l´écart entre deux points du réseau $$Δx = {lx\over N}.$$ N étant la longueur de notre système en lattice Boltzmann. On peut aussi définir Δt : $$Δt = {Δx\over c}.$$ et τ le temps de relaxation $$τ = {3Δtν\over Δx^2}+{1\over 2}$$.
Simulation de l´écoulement de Poiseuille entre deux plaques :
Un écoulement de Poiseuille décrit l´écoulement laminaire d´un fluide visqueux dans une conduite cylindrique. Il suit alors la loi de Poiseuille qui énonce la relation entre le débit d´un écoulement et les paramètres du fluide (viscosité, vitesse etc).
L´objectif de cette simulation est de mettre en évidence le profil de vitesse d´un écoulement de Poiseuille à deux dimensions.
On considère un fluide de viscosité égale à \(ν=15,6.10^{-6} m^2.s^{-1}\) (viscosité de l’air à 25°C) se diffusant entre deux plaques rectangulaires séparées d´une distance h, comme illustré dans la figure ci–dessous :
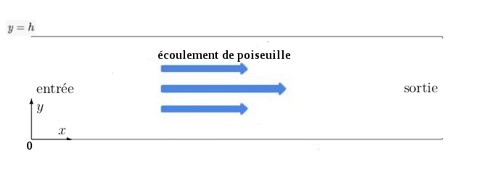
La simulation a été établie avec les conditions aux bords de rebond sur les parois exposées ci–dessus. On a imposé une vitesse nulle suivant l´axe y avec une petite perturbation «le bruit», et on injecte une vitesse constante en entrée et en sortie suivant l´axe x.
Cette vitesse est définie par la formule suivante :
\begin{eqnarray} v_x=v_{max}(\frac{4y}{h}-\frac{4y^2}{h^2}) \end{eqnarray} Avec \(v_{max}=0.1\) (sans unité en LBM) la vitesse maximale au centre du tube, c´est à dire en \(y=h/2\).
Ce profil, suivant l´axe x nous permet de maintenir un flux constant et adapté au tube.
Il dépend néanmoins de la largeur du tunnel et est parabolique, comparable à un profil de Poiseuille, comme illustré sur le graphe suivant :
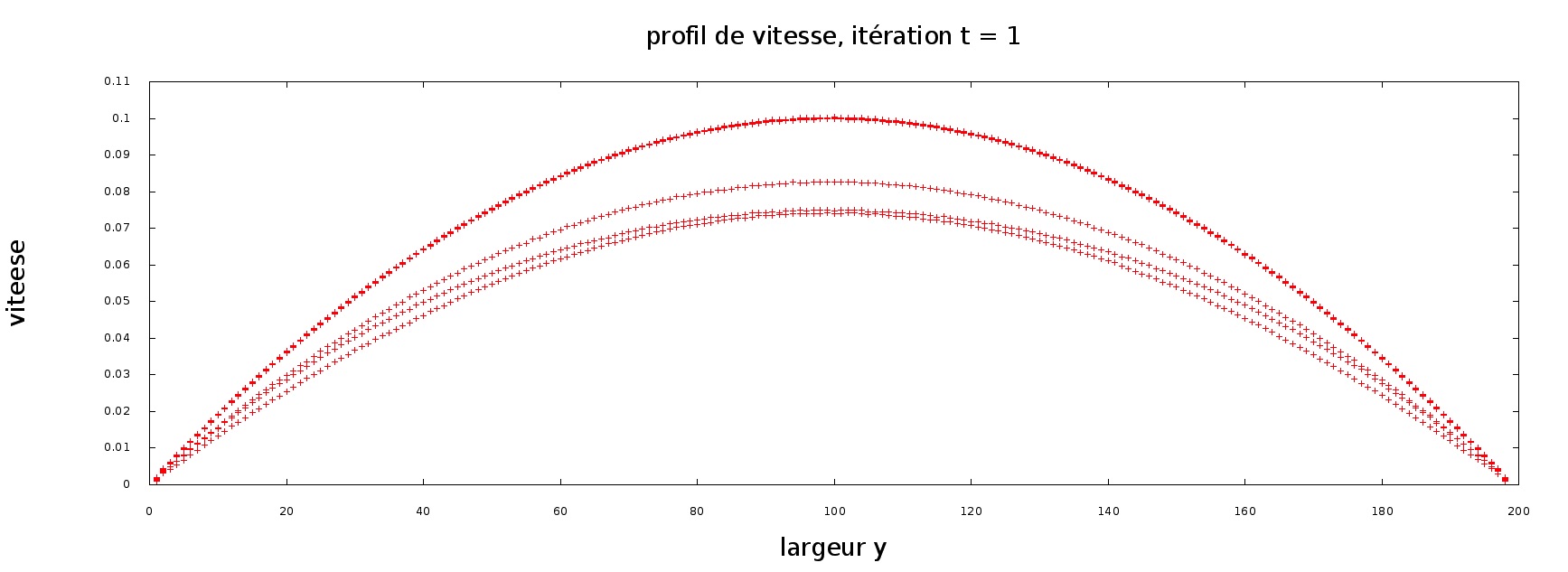
On remarque au début de la simulation que l´écoulement du fluide présente une légère anomalie. En effet, en entrée du tube une onde se propage sur tout le long et rebondit en sortie. Elle est dissipée du fait de la viscosité et disparait rapidement. Il s´agit en fait simplement d´une impulsion à l´initialisation du système.

