Résultats

Conditions aux bords périodiques et instabilités de Kelvin–Helmholtz

1. Mise en place des conditions périodiques




Pour pouvoir utiliser le schéma algorithmique, il est nécessaire de mettre en place des conditions aux bords et donc de prédire comment le fluide va se comporter lorsqu´il rencontre un solide. Une première ébauche de conditions aux bords et de poser qu´il n´y a pas d´extrémités à notre problème. On impose une périodicité aux extrémités afin de tester le bon fonctionnement du programme. Le principe de périodicité est simple. Lorsque le fluide entre en contact avec les délimitations de l´espace, il est envoyé de l´autre côté.

Prenons l´exemple de la fonction de distribution \(f_2\) de la méthode de Boltzmann sur réseau, qui se déplace uniquement vers le haut (vers les y positifs). Pour un espace de taille 200×100, qui fait donc 100 nœuds de largeur (y), lorsque l´on diffuse la distribution \(f_2\) située en (x, y=199) , la distribution se retrouve au pas suivant à la position (x , y=200), puis elle se retrouve de l´autre côté de l´espace en (x , y=0), puis (x , y=1)…




2. Un test simple : Kelvin–Helmholtz



• Dans la réalité



Lorsque deux couches fluides se trouvent en contact et que ces derniers ont des vitesses différentes, il peut se créer à l´interface des instabilités. Ce phénomène est étudié puis démontré par Lord Kelvin et Hermann Ludwig von Helmholtz. Il est lié à la viscosité et donc aux frottements issus du contact entre les deux fluides. Il existe ainsi une différence de vitesse critique à partir de laquelle on peut observer ces phénomènes.

Cette différence de vitesse dépend bien entendue du milieu considéré et des fluides en question, mais intervient généralement lorsque le nombre de Richardson, Ri<0,25.
Le nombre de Richardson est le rapport entre l´énergie potentielle gravitationnelle d´une quantité de fluide et son énergie cinétique. Ces phénomènes se retrouvent dans de nombreuses situations, mais sont facilement visibles dans l´atmosphère, où les conditions d´instabilités sont souvent remplies entre les couches nuageuses.







• Dans le programme (deux écoulements de sens opposés)




Au début de cette simulation nous avons édité un programme pour visualiser le phénomène physique des instabilités de Kelvin–Helmholtz introduit précédemment. Pour ce test, la vitesse est nulle partout sauf dans une large bande centrale où on impose une vitesse horizontale positive (vers la droite).
Aux deux interfaces (entre le fluide en mouvement et le fluide au repos) vont se créer des frottements dus à la viscosité, qui vont entraîner des instabilités semblables aux phénomènes étudiés par Kelvin et Helmoltz.






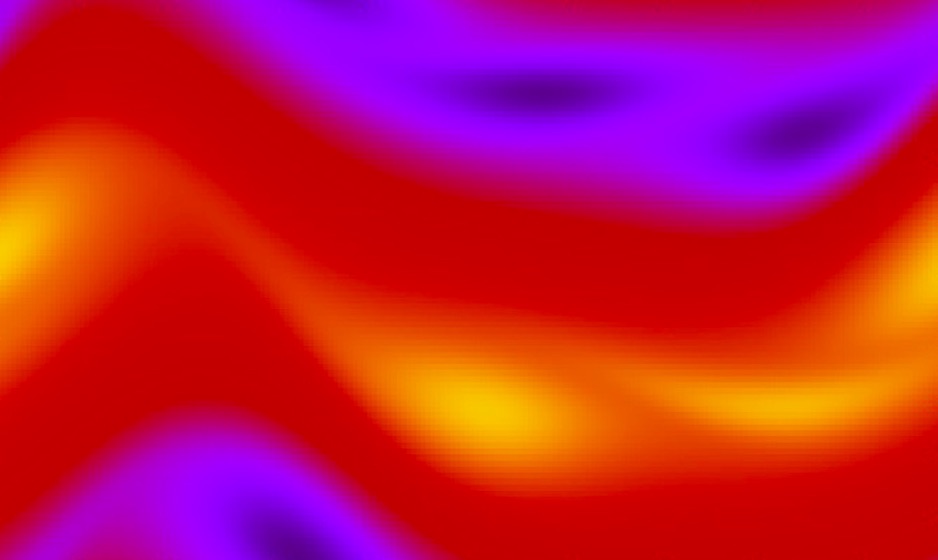
Vous trouverez plus de détails, et notamment des images qui montrent le développement des instabilités dans le rapport de stage, § 4.2 . Ce test permet dans les cas généraux de faire une étude qualitative du programme et de vérifier que dans des cas particuliers, les simulations convergent bien vers des résultats connus.

Premières vraies conditions aux bords : vers un régime réaliste

1. Mise en place des conditions aux bords réalistes




La mise en place de conditions périodiques (cf partie précédente) permet d´effectuer les premiers tests "visuels" du code. Les résultats obtenus semblent cohérents avec les phénomènes physiques qui se réalisent dans ces conditions (instabilités de Kelvin–Helmholtz).

Cependant, les conditions périodiques sont loin de correspondre à la réalité physique. En définitive, nous voulons être capables de simuler l´écoulement d´un fluide dans une portion de tube, avec des bords et deux extrémités. En s´inspirant de la publication de Y.Bao et J.Meskas d´avril 2011, nous avons donc mis en place des conditions aux limites plus réalistes.
Le principe de diffusion est toujours le même : Rappelons que le modèle de diffusion est constitué de 9 distributions de vitesses qui vont chacune dans une direction privilégiée à chaque étape de diffusion.
On se pose donc ensuite la question suivante: "Sur la position suivante se trouve–t–il un solide?".
Si ce n´est pas le cas, le programme fonctionne comme précédemment et la distribution se diffuse dans la même direction. C´est bien évidemment le cas où le fluide rencontre un obstacle qui nous intéresse.




2. Test du rebond sur les parois




Le principe que nous utilisons pour notre modèle de simulation est appelé en anglais "mid–grid bounce–back" que l´on pourrait traduire en français par "rebond sur mi–réseau". Voici ci–dessous une illustration qui permettra de vous éclairer un peu sur le sujet.





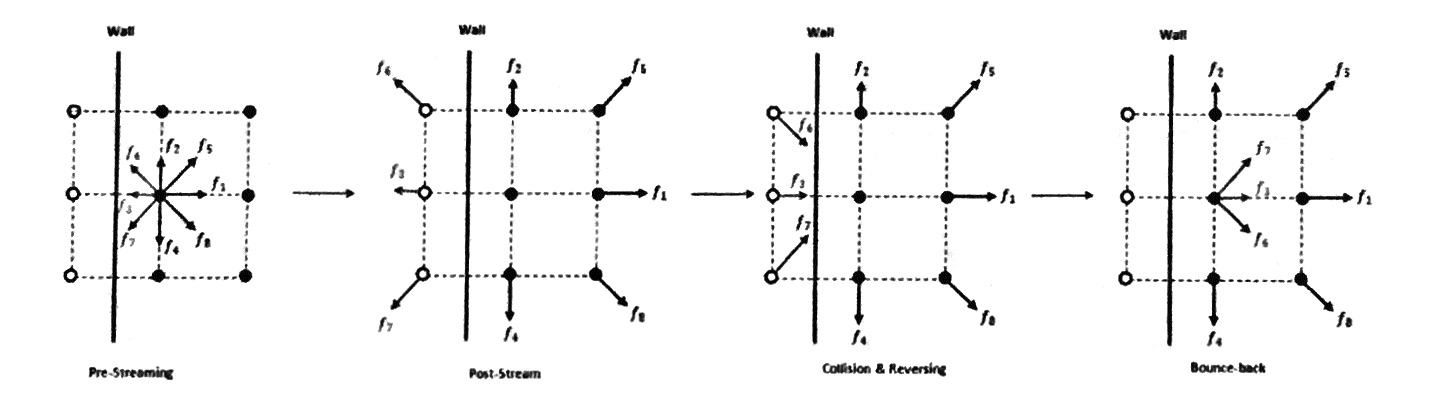
Comme vous pouvez le voir sur l´illustration, après l´étape de diffusion, les distributions qui ont passé un mur (ou tout autre obstacle) sont inversées (une distribution «N–O» se retournera vers le «S–E», cas de la distribution \(f_6\)), et elles sont replacées sur le nœud de départ. Ainsi, elles ont donc "rebondi" sur le mur pour être renvoyées.
Bien entendu, même si ce modèle reflète mieux la réalité que les conditions périodiques (qui rappelons le, ne servaient qu´à tester le programme), il n´est pas réaliste.

Dans un premier temps, il suppose que le choc est totalement élastique, il y a donc conservation de l´énergie cinétique.

De plus, sur une surface lisse, les particules ne se comporteraient pas forcément comme le font nos distributions : une particule envoyée sur un mur avec un angle de 45° avec ce dernier ne repart pas dans le sens opposé, il est bien plus logique que cette particule reparte avec un angle de 135° plutôt que de revenir à son point de départ.
N´oublions pas qu´il s´agit d´un modèle numérique qui tente de se rapprocher du modèle physique réel.

Ces nouvelles conditions aux limites mises en place, il est possible de traiter des problèmes plus intéressants qu´une simple interaction fluide–fluide comme dans la partie précédente. On cherche donc à étudier l´interaction entre le fluide et des solides (bords du tuyau, réseau, obstacles, murs).
Il convient bien entendu tout d´abord d´effectuer quelques tests après avoir modifié le code pour s´assurer que la simulation s´accorde avec la théorie.

Un premier test très simple consiste à envoyer une distribution de vitesse dans une unique direction et d´imposer des murs dans les deux sens. On affiche à chaque pas de temps la position (x,y) de la distribution sur le réseau et on s´assure qu´elle rebondit à l´endroit où des murs sont placés. C´est un petit test rapide qui nous permet de voir que les distributions se déplacent toujours convenablement (à la fois dans les directions horizontales et verticales, mais également en diagonales) en connaissant au préalable bien évidemment l´allure du résultat.

Régimes laminaire, transitoire, turbulent (Von Karman)

Maintenant que le code a pu être vérifié par des tests simples, le travail se concentre sur l´expérimentation et la simulation de divers problèmes. Pour définir le type d´écoulement, il faut prendre en compte la géométrie du problème, la vitesse de l´écoulement et les caractéristiques du fluide (viscosité). Pour cela, Osborne Reynolds introduit en 1883 une quantité sans dimension qui portera son nom, le nombre de Reynolds. Il s´agit du rapport entre les forces d´inertie et les forces visqueuses. Le nombre de Reynolds (Re) rend compte du régime d’un écoulement. Ce dernier peut–être laminaire à faible nombre de Reynolds, transitoire ou alors totalement turbulent (à grand nombre de Reynolds). Notons que ce nombre est une quantité numérique qualitative plutôt que quantitative. $$Re={U*L\over ν}.$$

• \(U\) : vitesse caractéristique du fluide \((m.s^{-1})\)
• \(L\) : longueur caractéristique du problème \((m)\)
• \(ν\) : viscosité cinématique du fluide considéré\((m^2.s^{-1})\)



La valeur du nombre de Reynolds dépendant du choix de ces grandeurs caractéristiques, les valeurs que nous obtiendrons seront à comparer entre elles plutôt qu’avec des valeurs de référence.

Il est intéressant de noter que le nombre de Reynolds est invariant suivant le modèle, c´est–à–dire que si deux écoulements sont géométriquement identiques mais pas de même taille, ils auront la même solution de vitesse et de force de trainée si le nombre de Reynolds reste le même. C´est la loi de similitude. En d´autres termes, le nombre de Reynolds reste globalement le même lorsque l´on change l´échelle d´une expérience. Ce nombre est donc très utile pour étudier les phénomènes physiques sur des maquettes d´objets ayant une taille réelle trop grande pour faire ces études en laboratoire. Cela signifie donc aussi que dans le cas d´une simulation numérique on peut tout aussi bien utiliser les quantités physiques du phénomène que celles adimensionnées du programme pour déterminer le nombre de Reynolds.

Pour calculer le nombre de Reynolds, nous utilisons les quantités suivantes : la viscosité du fluide, qui est fixée, la vitesse définit comme étant la vitesse maximale du profil de vitesse de Poiseuille et enfin la largeur de l´espace. En augmentant la vitesse sans changer les deux autres quantités, il est évident que le régime de l´écoulement sera de plus en plus instable et donc que le nombre de Reynolds augmentera. On peut donc distinguer les différents régimes en fonction du nombre de Reynolds



1. Régime Laminaire à petits nombres de Reynolds (Re<10)




Un écoulement est dit laminaire lorsque la majorité du fluide s´écoule dans une seule direction, c´est le régime le plus stable. Dans ce régime, en présence d´un obstacle, le fluide va en faire le tour et continuer son chemin.








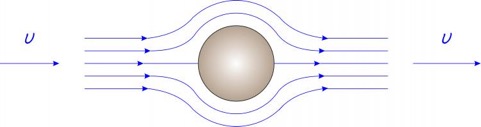
Résultats de la simulation:



Re=7,4








2. Régime Transitoire (10<Re<185)




En régime transitoire commence à se former des tourbillons à l´arrière de l´obstacle. Le régime n´est plus stable comme pour l´état laminaire mais n´a pas passé un seuil critique d´instabilité. Pour le cas d´un obstacle unique circulaire au milieu du tube, on observe généralement dans ce régime la formation de deux vortex tournant en sens opposé à l´arrière de l´obstacle.








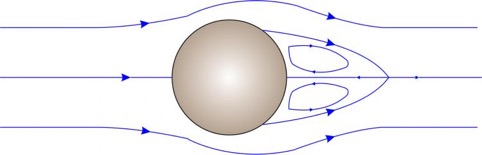
Résultats de la simulation:



Re=74








3. Allées de tourbillons de Von Karman (Re>185)




Lorsque l´on augmente encore la vitesse d´écoulement dans le tube, les instabilités s´intensifient et les deux tourbillons présents à l´arrière de l´obstacle se détachent alternativement. On observe ce que l´on appelle des allées de Van Karman. Ce phénomène est relativement courant dans la nature, notamment lorsqu´une couche de fluide (nuages) en mouvement rencontre un obstacle, comme une montagne.



• Résultats attendus














• Résultats avec animations :



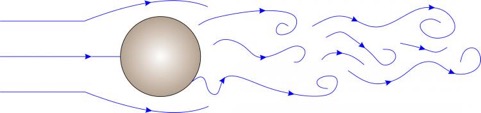
Re=259









4. Régime totalement Turbulent et limite du programme




Lorsque les instabilités se renforcent encore, le régime devient totalement turbulent. Il n´y a alors plus aucune symétrie dans l´écoulement.







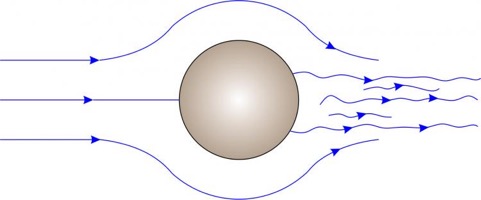
Pour nous, c´est là que notre code atteint sa limite. Étant donné que le programme reste stable uniquement pour un petit nombre de Mach (rapport entre la vitesse du fluide et la vitesse du son dans le milieu), augmenter encore la vitesse revient à violer cette règle. Dans ce cas, le programme n´est plus en mesure de simuler l´écoulement et nous renvoie systématiquement des résultats faux. Le programme permet donc d´afficher des écoulements stables (laminaires) jusqu´à des écoulements relativement instables (Von Karman) mais il n´est pas possible d´atteindre un régime totalement instable et turbulent comme le montre l´illustration ci–dessus.

Autre résultat intéressant: Le trou dans un mur

1. Résultat attendu : formation de vortex sur les côtés




Il est possible d´étudier d´autres géométries intéressantes de notre problème afin de tester le bon fonctionnement du programme. Bien entendu, à réaliser des montages trop compliqués, il nous est impossible de prévoir des résultats et donc d´attester de la viabilité physique de la simulation. Un montage intéressant en terme d´écoulement consiste à placer un mur de la largeur du tube sur le trajet du fluide, et de l´ouvrir en son centre. Lors de l´écoulement, on peut s´attendre à la formation de tourbillons, tournant en sens inverse à chaque bord du trou, tourbillons qui à partir d´une certaine vitesse du fluide, vont se détacher et rester dans la section de tube sans en sortir, plaqués par le flux constant qui passe par le trou.







2. Résultat obtenu

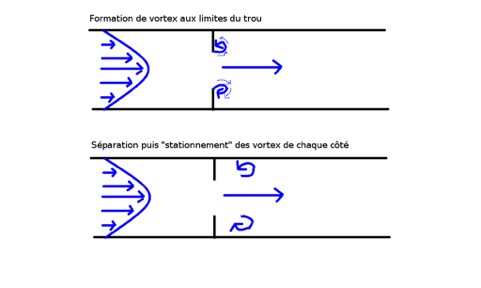
Conclusion

La méthode de Boltzmann sur réseau est une façon efficace de répondre aux questionnements concernant la façon dont un fluide s´écoule dans un tube. Durant notre projet, nous nous sommes concentrés sur la réalisation d´un code mettant en œuvre cette méthode pour un écoulement bidimensionnel et nous avons été capables de retrouver des résultats cohérents avec la réalité. Par exemple, nous avons été capables de simuler des instabilités de Kelvin–Helmholtz, d´établir un profil de vitesse de Poiseuille ou encore de perturber un écoulement en posant des obstacles sur le chemin du fluide (Von Karman).

Le principal défaut de la méthode de Boltzmann sur réseau est qu´à partir d´un seuil critique de stabilité, ce modèle ne fonctionne plus. Le modèle impose en effet un petit nombre de Mach, Ma<<1, c´est–à–dire une vitesse du fluide petite devant la vitesse caractéristique du réseau qu´est la vitesse du son. Le modèle de Boltzmann sur réseau est limité à des fluides incompressibles.

Cependant, la LBM a des avantages non négligeables. Elle est facilement mise en place pour des écoulements simples et permet de représenter des profils d´écoulements non triviaux, tels que l´écoulement à travers un réseau périodique ou le passage dans un goulot d´étranglement.
La mise en place de telles techniques permet d´étudier l´effet d´un fluide sur une structure et d´en tirer des données physiques, qui peuvent être utilisées pour parfaire
l´aérodynamisme d´une carrosserie par exemple.