Résultats

Nous avons utiliser Matlab pour traiter les données et comprendre comment les particules collisionnent entre elles dans le sillage d'une grosse sphère pour un nombre de Reynolds $Re=200 $ pour le cas laminaire et $Re=1000$ pour le cas turbulent, et nous avons réussi à visualiser le champs de vorticité pour chaqu'un de ces deux type d'écoulement , ainsi que les positions de collisions des petites particules et ce nombre en fonction de leurs tailles, et la moyenne de ce nombre en fonction de de la distance r de l'axe de symétrie $z$
Voici les résultats obtenus :

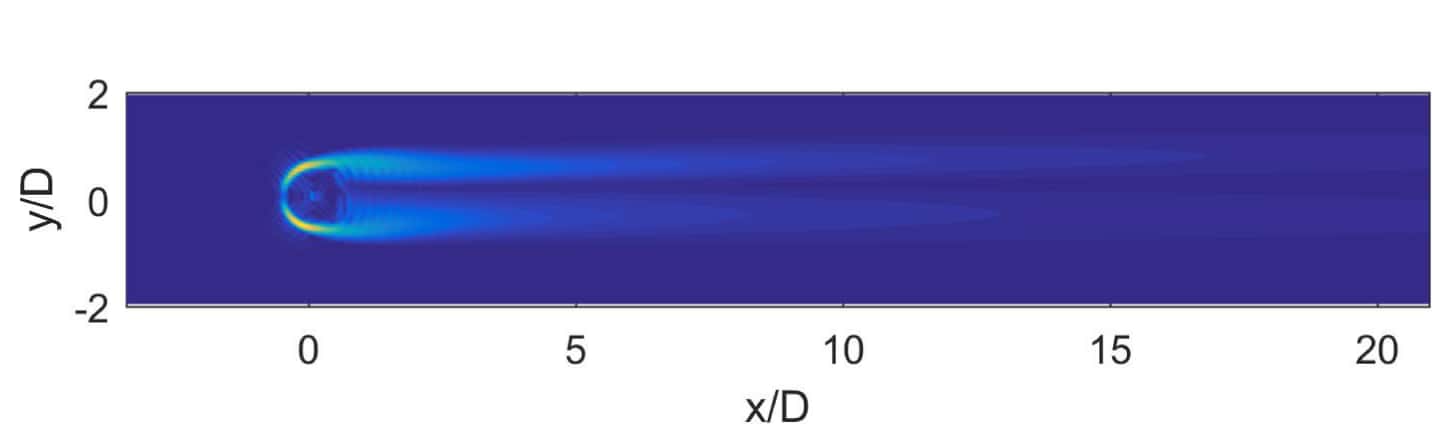
Visualisation du champ de vorticité pour les deux types d'écoulements

On remarque un écoulement quasi stationnaire et un écoulement de sillage turbulent pour le cas turbulent.

influence de la taille des petites particules sur le nombre des collisions

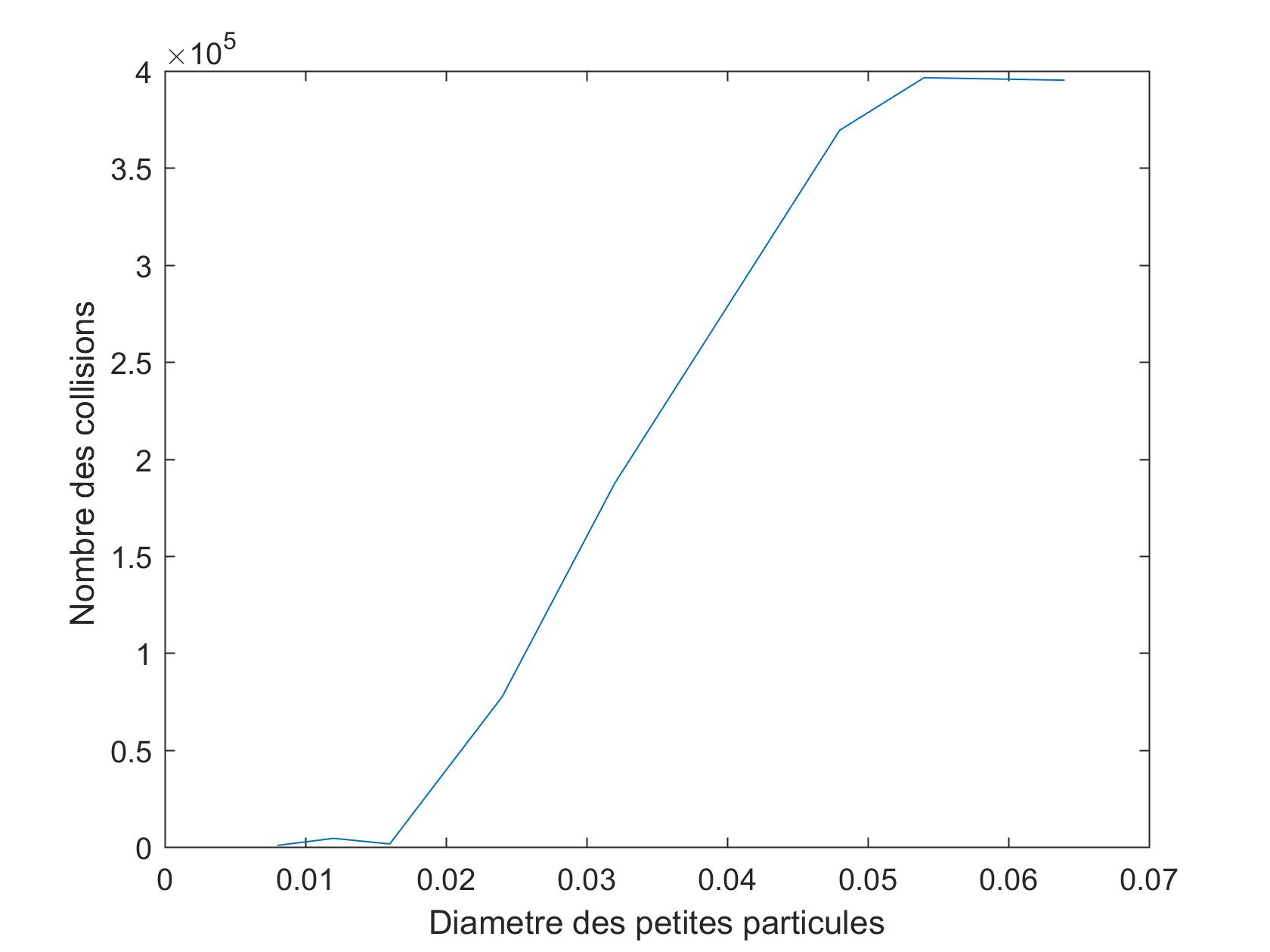
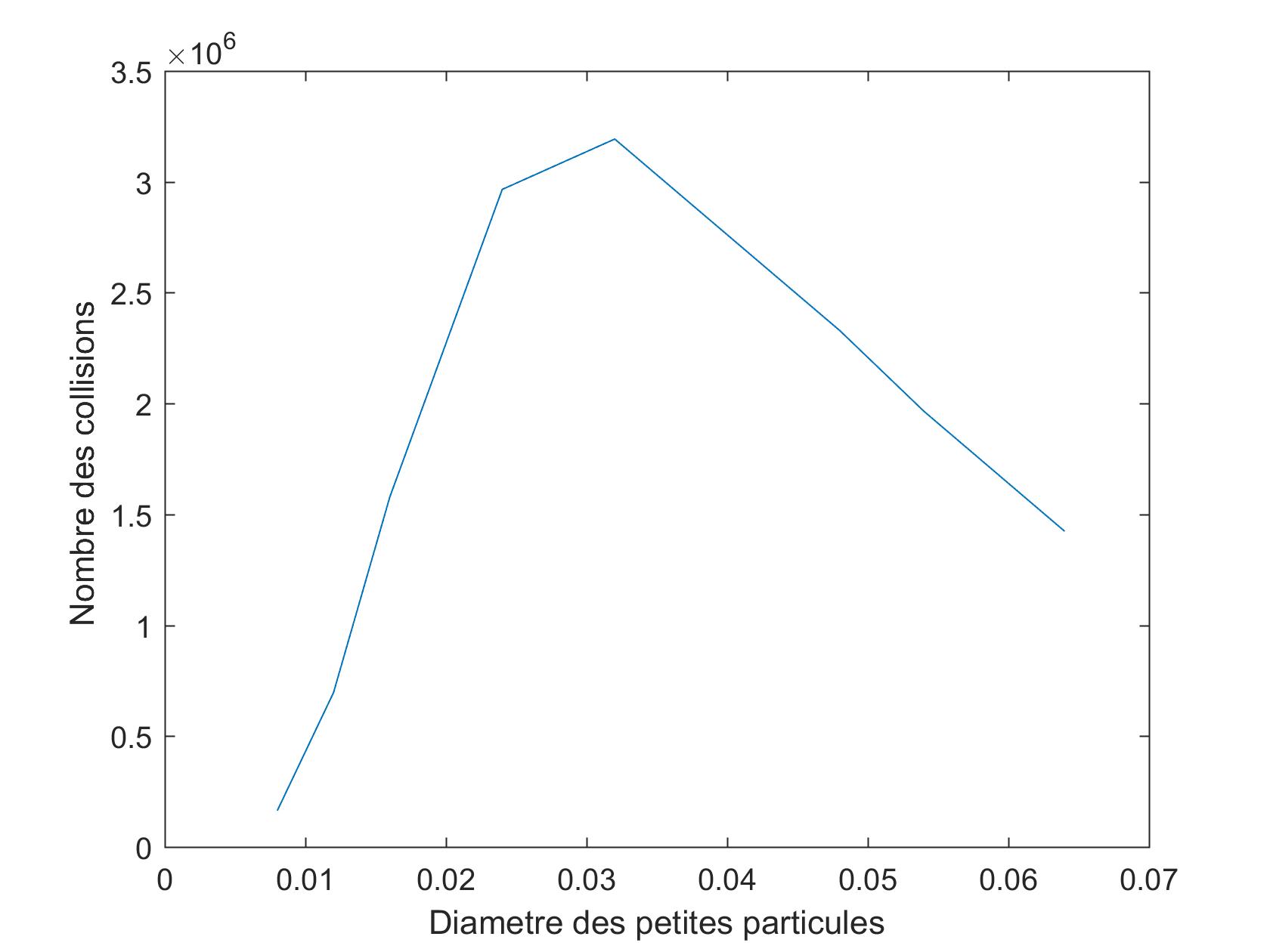
Une résultat qui montre l'influence de la turbulence sur les collisions des petites particules .

Les deux figures suivantes montrent le nombre total de collisionen fonction de la taille des petites particules pour le cas laminaire (à gauche) et pour le cas turbulent (à droite).
Pour un sillage laminaire, la probabilité de collision augmente de façon monotone avec la taille des petites particules. Dans le cas turbulent la probabilité a un maximum indiquant une sorte de résonance. Mais encore plus important, on observe que l'on enregistre beaucoup plus de collisions dans le sillage turbulent.

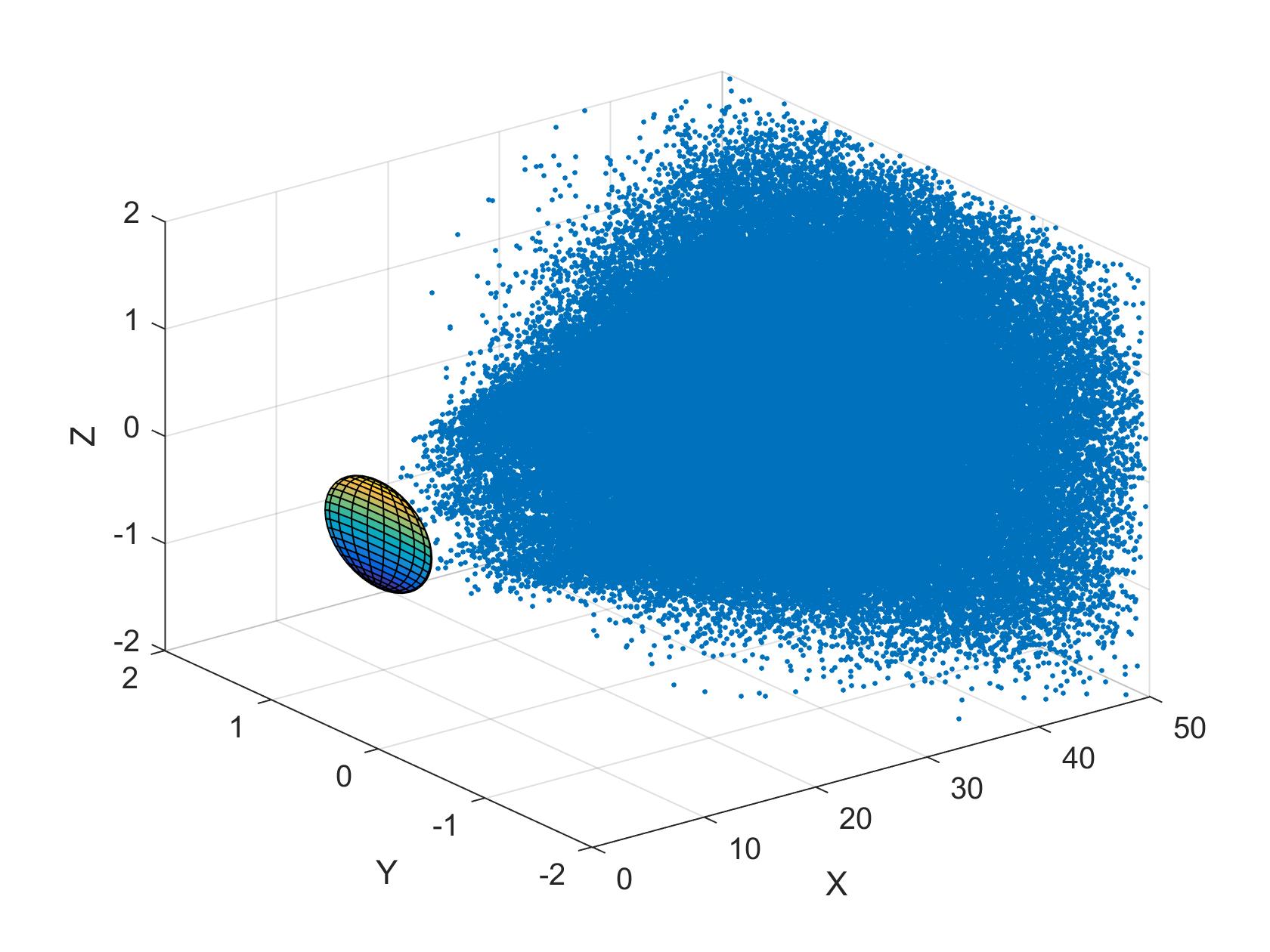
Positions des collisions

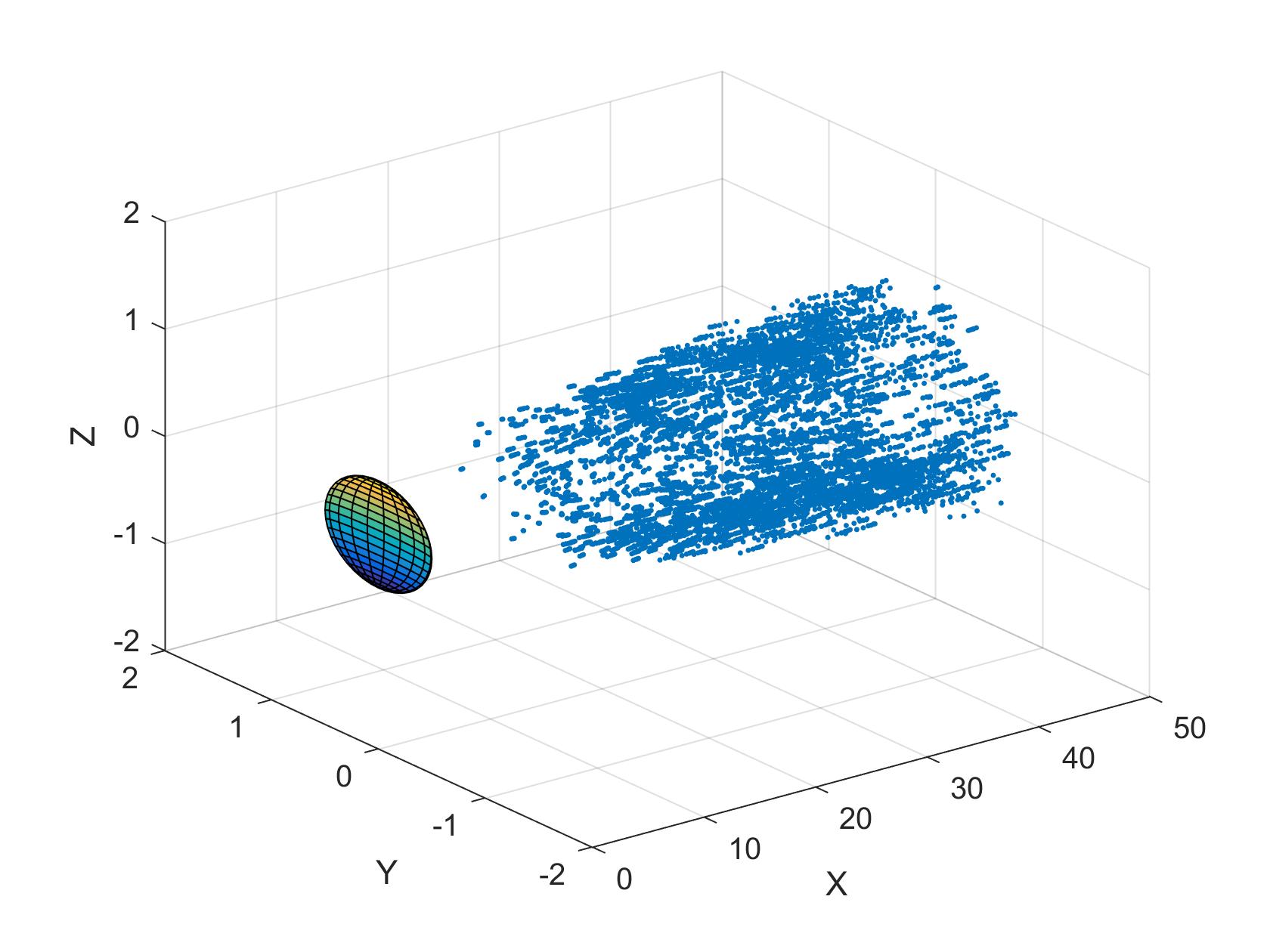
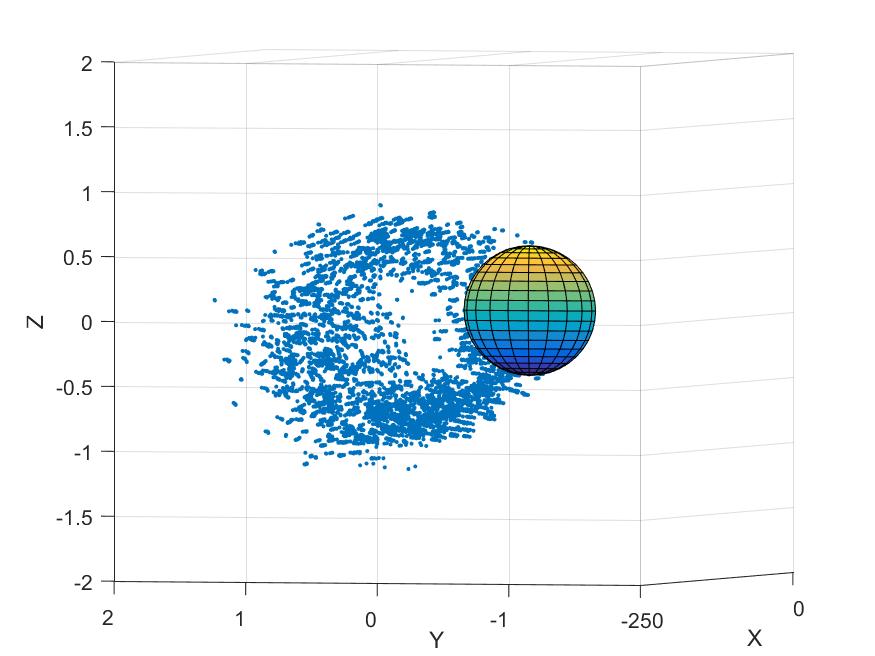
Elles sont visibles par des petits points bleues dans les figures suivantes (laminaire toujours à gauche et turbulent à droite).


On observe que les collisions ont eu lieu dans une zone serrée derrière la grosseparticule dans le cas laminaire et que cette zone et beaucoup plus large dans le turbulent. On peut supposer que ce sont les tourbillons du sillage turbulent qui augmentent fortement le nombre de collision et disperse leurs positions. Si on observee une de ces deux dernières figures d'une côté différente :

On remarque que la distribution des collisions est différente , c'est comme s'il n'y a pas beaucoup de collision juste derrière la grosse sphère , et cela nous a invité a moyenner le nombre des collisions autour de l'axe de symétrie .

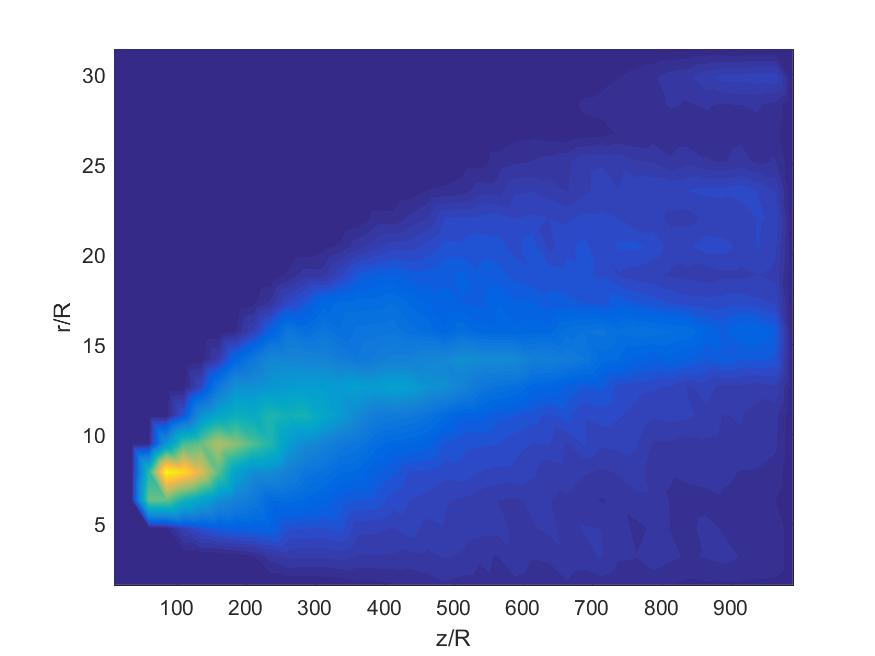
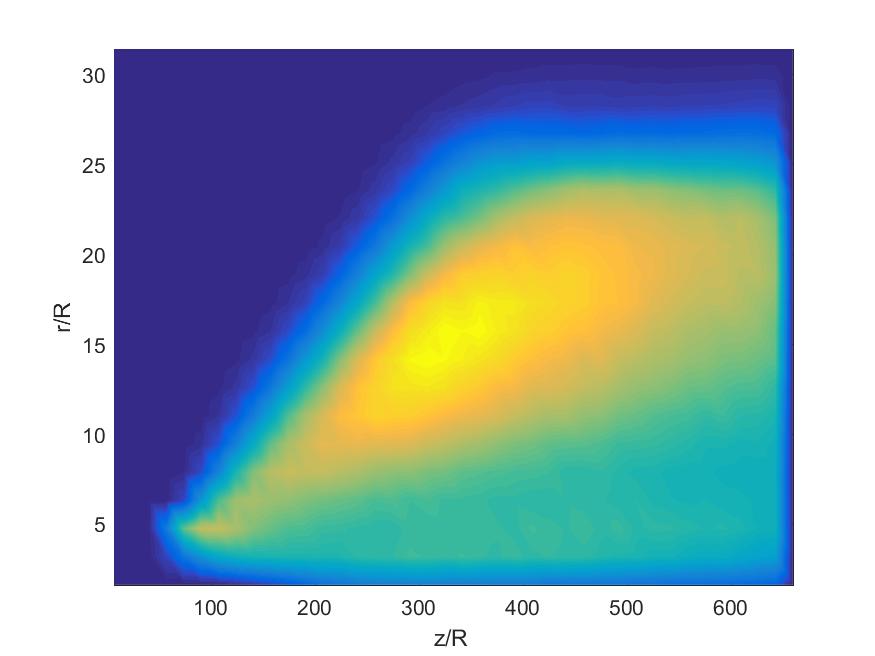
probabilité de collision moyenne

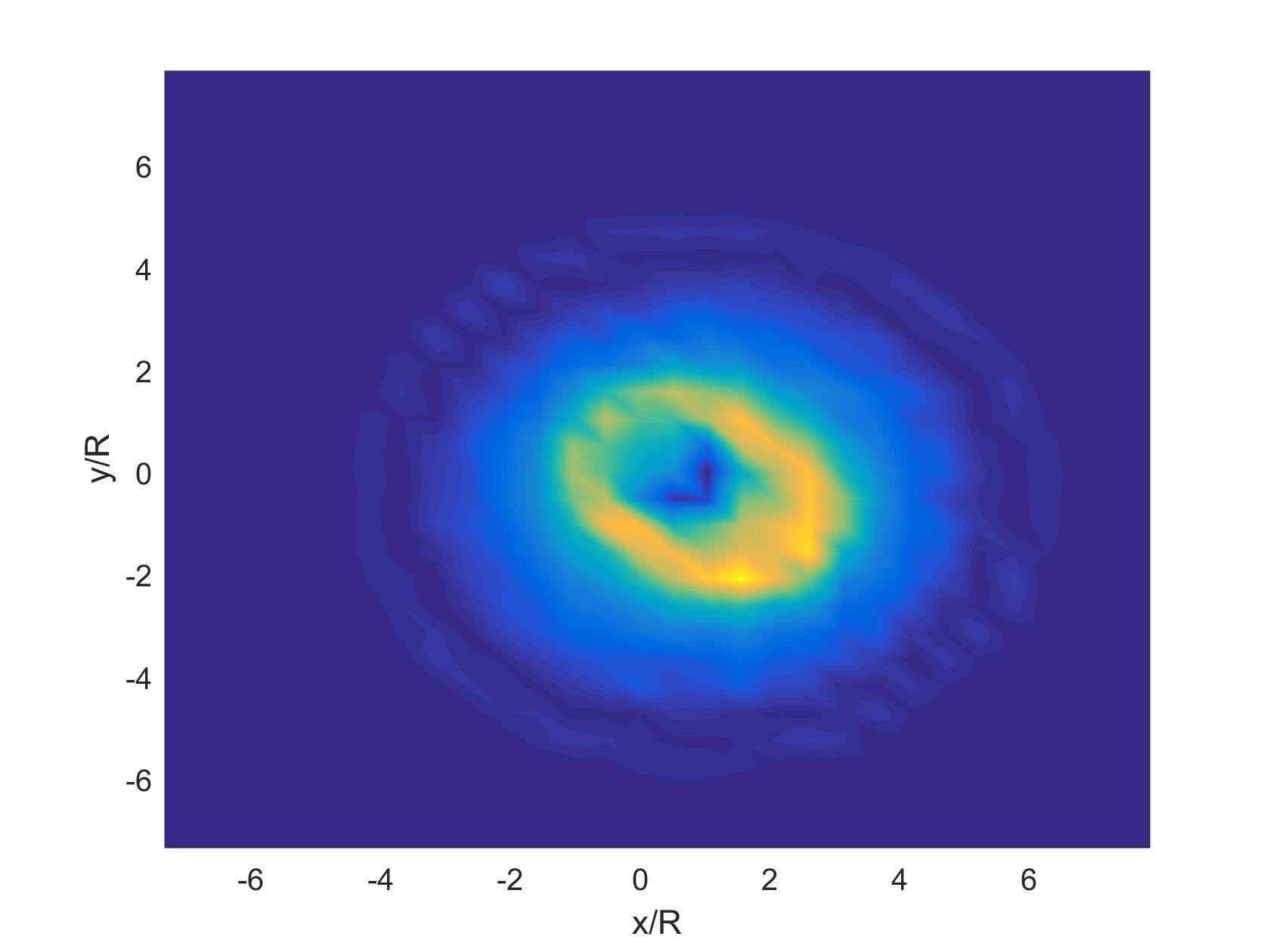
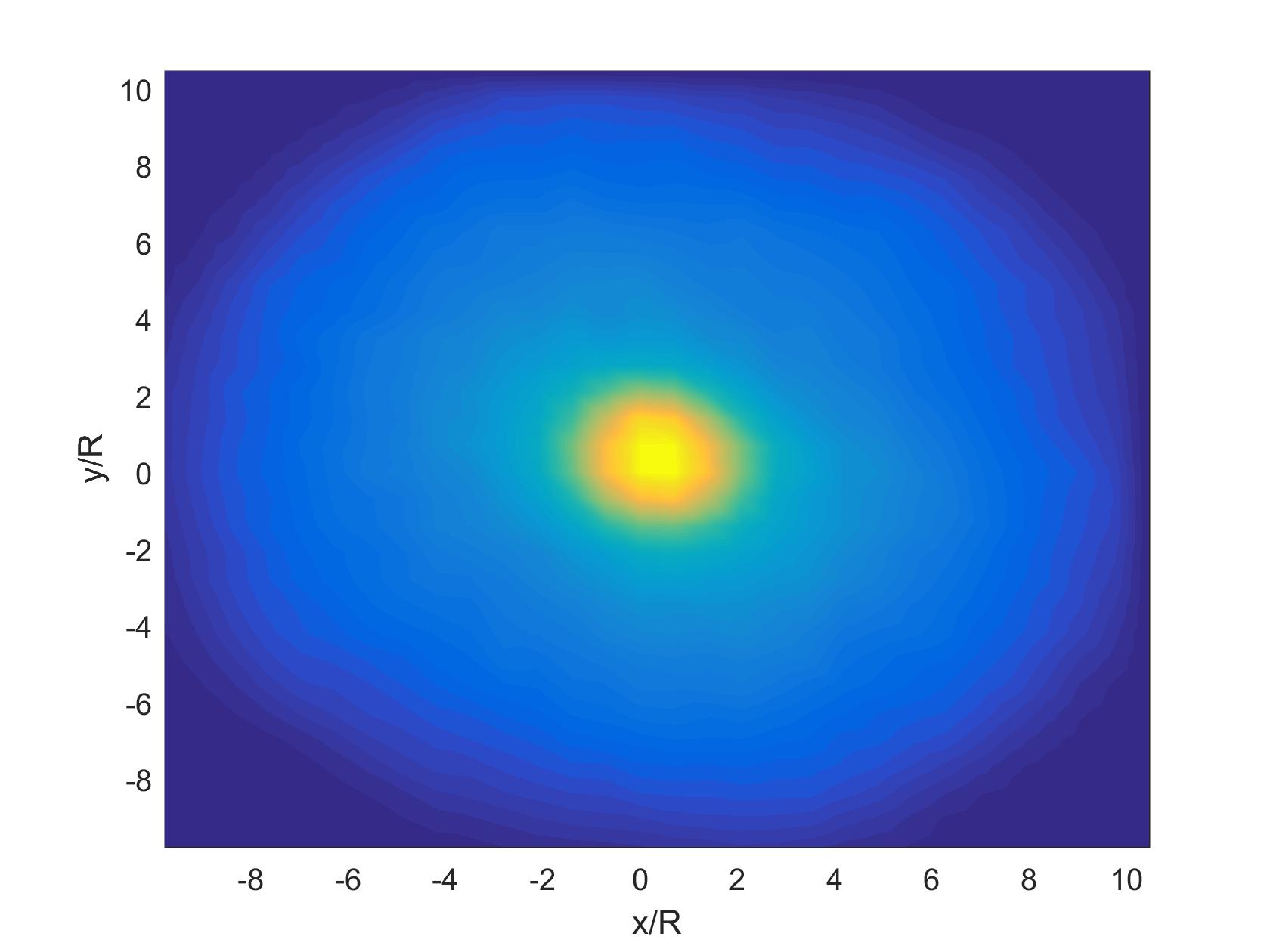
La probabilité de collision, pour une collision dans le cas laminaire (figure à gauche) est maximal très proche de la grosse sphère. C'est dans la couche limite avec ces grands gradient que les petites particules se rencontrent le plus. C'est diffèrent dans le cas turbulent (figure à droite). Ici, le maximum se situe dans le sillage. Ce sont alors les tourbillons qui créent des collisions.
Voici une autre resultat de vue de face sur le plan (x,y)

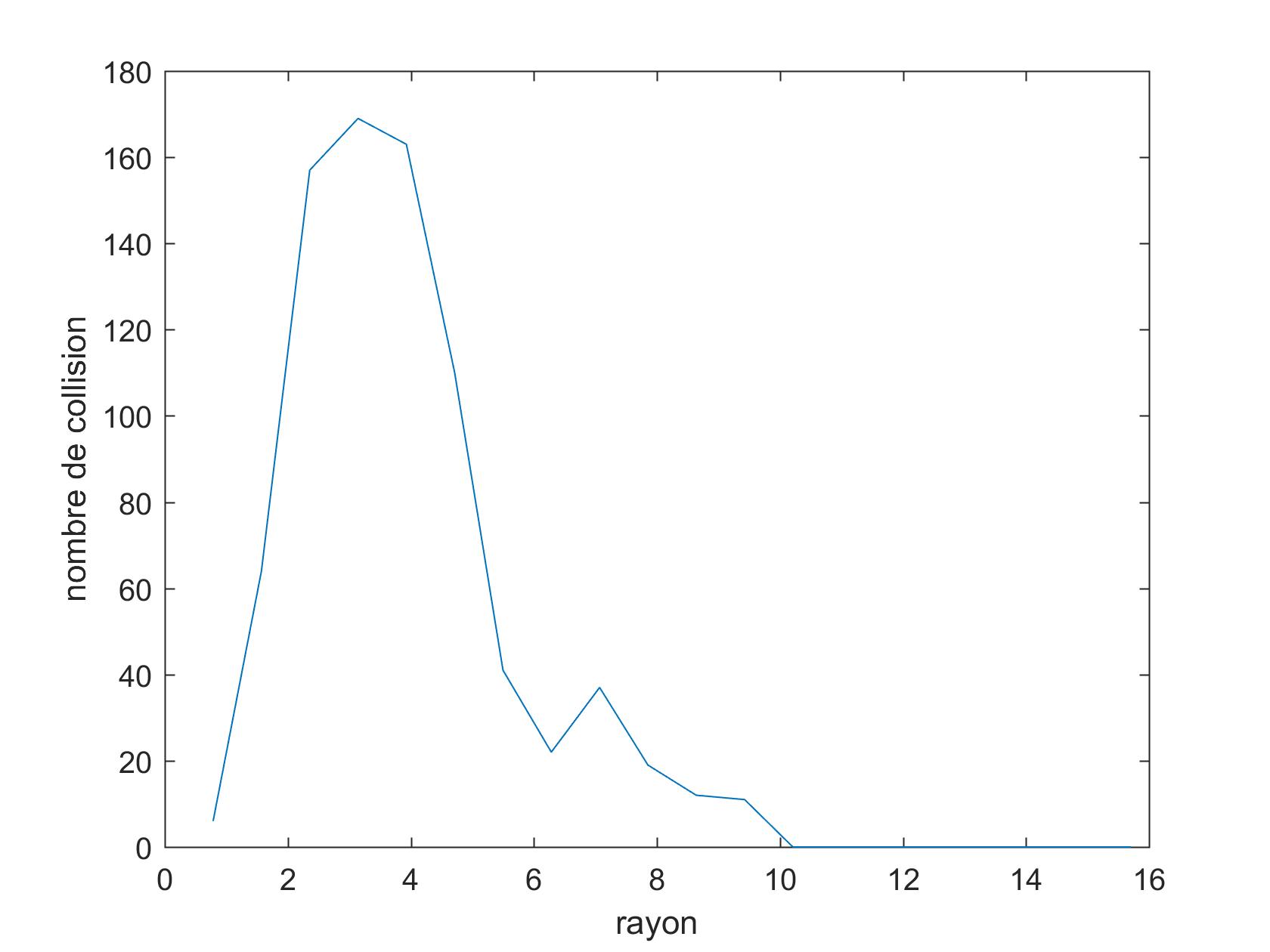
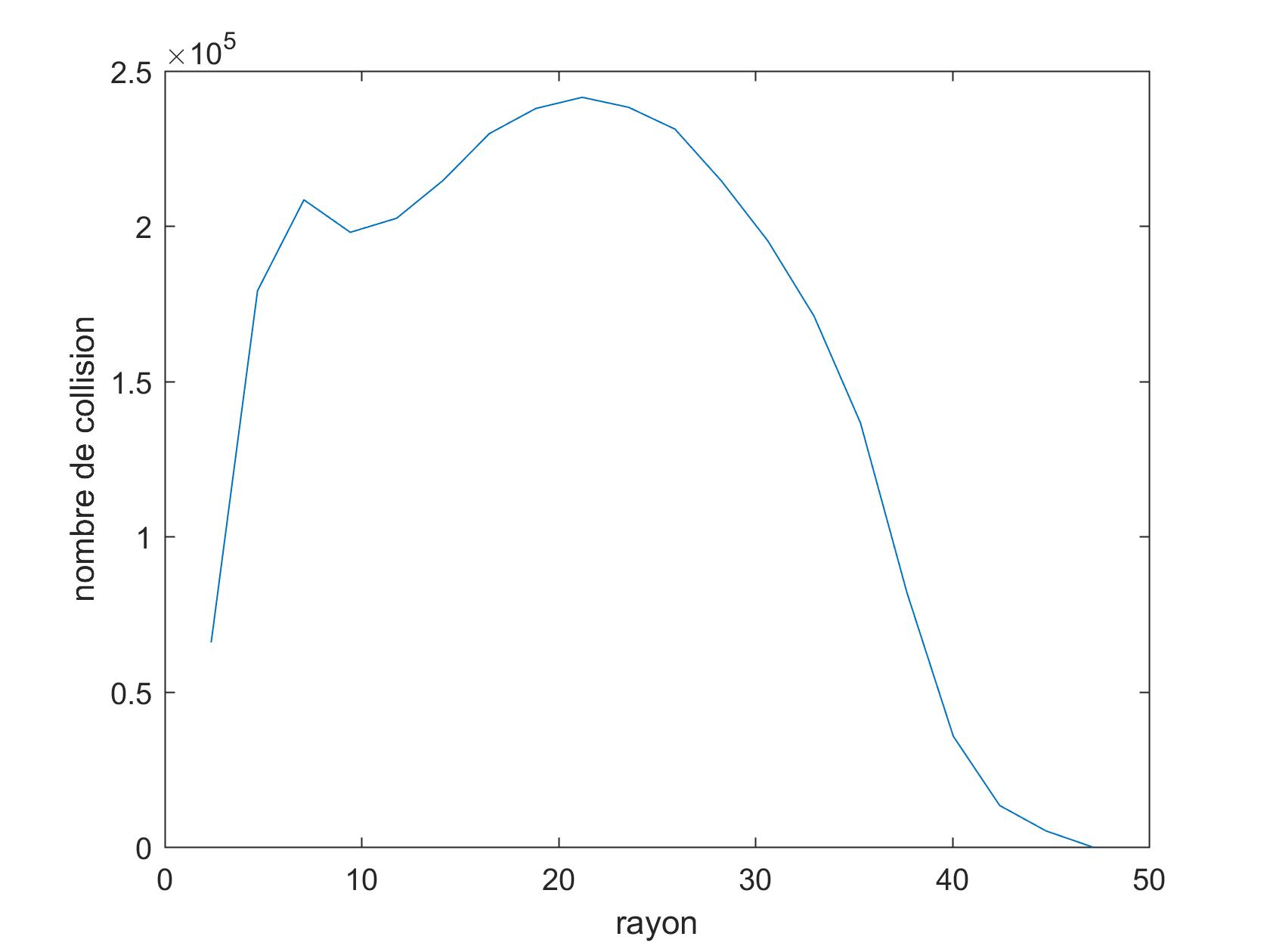
moyenne du nombre de collision en fonction de rayon

ici le rayon r est la distance qui sépare l'axe de symétrie à un point donné, ce rayon est défini par $r=\sqrt {x^2+y^2}$

Conclusion:

Pour conclure, notre objectif etait de comprendre comment le passage d'une goutte dans un nuage peut influencer les petites gouttelettes de ce dernier, nous avons essayé de comprendre les différents types d'écoulement, modeliser théoriquement et numériquement le système et enfin d'analyser les données des simulations issues de ce travail numérique. Et nous avons pu déduire que la taille des petites gouttelettes influence le nombre des collisions et que plus le sillage est turbulent plus on le nombre des collisions est important. Nous avons aussi à reuissi à apprendre que la probabilité des collisions dans le domaine change selon le type de sillage.