Mesure statique du Module de Young
Avant de pouvoir se pencher sur le coeur du problème, il nous faut caractériser les éléments, et notament la sagaie qui est notre objet déformable. Un des paramètres importants dans ce phénomène est la fréquence propre de la sagaie, c'est à dire la fréquence à laquelle elle vibre quand elle est dans son premier mode propre. Pour estimer cette valeur, nous avons choisi deux approches, la première étant de mesurer le module de Young par la mesure de la flèche.
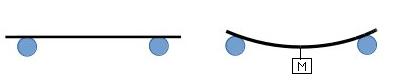
Il s'agit de poser le projectile sur deux points d'appui à une distance connue, puis imposer un poids en son centre. Alors que le projectile ploie, on mesure la "flèche" qui est la distance parcourue par le centre de la sagaie lors de la flexion. Connaissant la distance entre les appuis, le poids donc la force appliquée, les dimensions de la section du projectile le module de Young est donné par la relation suivante:
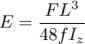
Avec F la force : le poids de la masse que nous suspendons à la sagaie (appliquée au centre des points d'appui), L la distance entre appuis, f la flèche et Iz le moment quadratique suivant l'axe normal au plan d'experience.
Déduction de la fréquence propre
Maintenant que nous avons pris en compte les dimensions de la sagaie, ainsi que son module de Young avec l'hypothèse que notre projectile est une poutre cylindrique pleine. On peut alors en tirer les fréquences propres pour le 1er mode de vibration grâce à la relation :
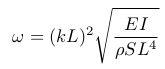
Avec L la longueur de la sagaie, E le module de Young, I le moment quadratique suivant l'axe normal au plan de flexion passant par la fibre neutre, ρ la densité de la poutre, S la surface de sa section et (kL)² une constante que nous prenons pour le régime libre libre = (4,73004)2.
Les résultats obtenus avec cette démarche sont :
| Taille de la sagaie | Module de Young | Fréquence |
| Petite | 9.41 GPa | 15.72Hz +/- 1,5 |
| Moyenne | 8.26 GPa | 12,18Hz +/- 0,1 |
| Grande | 7.60 GPa | 11.14Hz +/- 0,4 |
