Préparation d'un état initial (résolution de Boltzmann en statique)

1. grid_ff La résolution de l'équation de Boltzmann nous donne les fonctions de répartition des atomes dans l'espace des phases. Dans un premier temps, le code résout l'équation (17) en minimisant 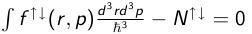à l'aide de broyden. Dans un second temps, une simple intégration sur les impulsions permet d'obtenir les densité (=nombre de particules par case). Il est facilement possible de représenter les densité en fonction de deux coordonnées sur un graphe en 3D. Densité des particules


2. vlaini.c A partir des densités,calculé ci-dessus, on détermine de manière aléatoire les positions dans l'espace des phases de chaque particule.

Dynamique du gaz (résolution de Boltzmann en dynamique)

Vla.c calcul les forces dues au pièges et aux intéractions entre les deux spins différents sur chaque particules et en déduit les nouvelles impulsions.

A partir des positions-impulsions calculé précédemment, on recalcule les densités sur la grille Puis, on détermine les forces sur chaque point de la grille (force).

A partir de ces forces, pour appliquer à chaque particule, on fait une interpolation tridimensionnelle (pour donner une idée cela ressemble à un barycentre où les poids des différents forces sont la distance avec la particule).

Dans cet exemple en 2 dimensions, la force appliquée à la particule:

• Fx=(Fx1 x Dx1)+(Fx2 x Dx2)
• Fy=(Fy1 x Dy1)+(Fy2 x Dy2)

Enfin, push applique ses forces sur les particules, modifiant leur impulsions. Les chocs, ayant un comportement différant seront étudiés plus en aval.