La propriété qui permet de déterminer si un gaz a un comportement quantique est la longueur d´onde de De Broglie :

Avec :
- p : quantité de mouvement de la particule
- m : masse de la particule
- T : température
- KB : constante de Boltzmann
Lorsque les fonctions d´onde des particules commencent à se recouvrir c´est–à–dire lorsque la longueur d´onde de De Broglie associée aux particules est de l´ordre de grandeur de la distance interparticulaire, la mécanique quantique influence les propriétés macroscopique, on dit que le gaz est quantique.
Le photon de masse nulle est donc une particule quantique quelques soient les conditions.
Dans notre cas, nous travaillons avec un gaz de rubidium, de masse non nul. Le seul autre paramètre modifiable est la température. On doit donc avoir λ de l´ordre de grandeur de l´ atome de rubidium (quelques Å).

On a donc besoin d´un gaz à une température de l'ordre du μK : un gaz froid.
Dans notre expérience, nous utiliserons un MOT (magnetic optical trap) ou piège magnético–optique dont le but est de refroidir les atomes et de créer un piège de potentiel V=(m/2)r2ω2 avec r, la distance au potentiel minimal supposé égal à zéro, ω, la fréquence du potentiel.
Pour refroidir les atomes, c´est–à–dire les ralentir, on utilisera les lasers. Le principe est basé sur l´échange d´impulsion entre les photons et les atomes.
Soit un atome qui se déplace à la vitesse v0 dans une onde laser de fréquence ν:
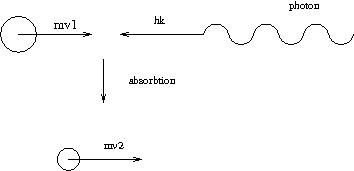
L´impulsion de l´atome dans l´étape 2 est :
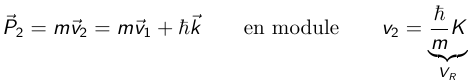
Après l´étape 2, l´atome passe à un état 3 : l´émission aléatoire d´un photon
 S
S
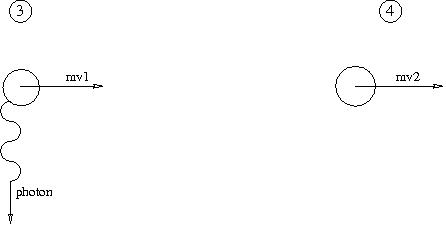
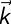 S : vecteur d'onde du photon émis spontanément dans une direction aléatoire de même module que
S : vecteur d'onde du photon émis spontanément dans une direction aléatoire de même module que 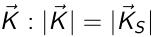
Si le processus est répété n fois, la vitesse finale de l'atome est :

La direction de
 S étant aléatoire, sa moyenne est nulle :
S étant aléatoire, sa moyenne est nulle :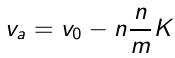
Exemple du sodium : λ=852 nm, vr=3,5 m/s.
A températute ambiante, la vitesse moyenne est d'environ 300 m/s et la durée de vie d'un état excité est de 3.10-7 s : le processus se répète 3.106 fois par seconde.
L'atome peut être arrêté en quelques dixième de seconde.Cette méthode est envisageable pour réduire la vitesse des atomes.
Outre le spin, la principale différence entre les bosons et les fermions concerne le principe d´exclusion de Pauli ( deux particules ne peuvent avoir le même état quantique), seuls les fermions y obéissent.
- Les bosons Un boson est une particule de spin entier qui obéit à la statistique de Bose–Einstein :
- Les fermions
- Un fermion est une particule de spin demi–entier qui obéit à la statistique de Fermi–Dirac :
l´électron en est un exemple.
De part leur obéissance au principe de Pauli, deux fermions ne peuvent se trouver dans le même état quantique ( position, énergie, spin,etc ).
Un gaz de Fermi dont la température est nulle, donc d´énergie totale minimum est dit complètement dégénéré. Les particules occupent les niveaux les plus bas mais elles ne peuvent pas se trouver dans le niveau le plus profond à case du principe d´exclusion de Pauli. On va donc disposer les N particules sur les niveaux de manière indivuduelle en partant de l´état le plus bas et en respectant le principe d´exclusion de Pauli.
Pour un spin de particule égale à s, on peut mettre 2s+1 particules sur chaque niveau de particule individuelle.
Le niveau d´énergie occupé le plus haut s´apelle le niveau de Fermi EF. Comme indiqué plus haut, les fermions obéissent à la distribution de Fermi–Dirac.
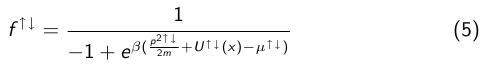
Avec :- εi : énergie du micro état :
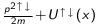
- μ : potentiel chimique de la particule
- β=1/(kBT)
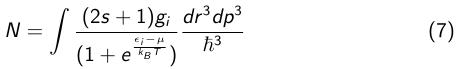
- εi : énergie du micro état :
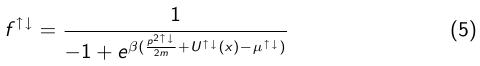
A une température proche du zéro absolu, les bosons peuvent se trouver exactement dans le même état quantique, formant un gaz quantique appelé condensat de Bose–Einstein, les particules ayant la même fonction d´onde ont le même comportement que des photons dans un laser(lumière cohérente ...). La première observation d´un tel état a eu lieu en 1995 suite aux travaux d´Eric Cornell et Carl Wieman qui refroidirent un gaz de rubidium à des températures de 170 nanokelvins.
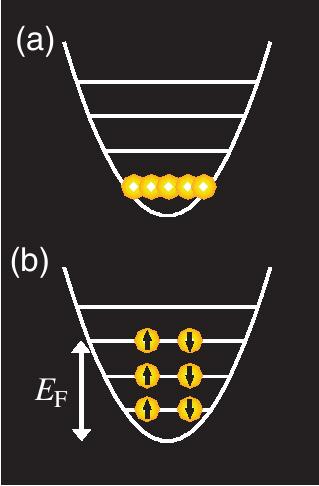
Etat fondamental d'un gaz de bosons (a) et de fermions de spin ½ (b) piégés.
Tout comme en physique classique, l´étude d´une collision entre deux particules quantiques de masse m peut être représentée comme la diffusion d´une particule fictive de masse μ=m/2 évoluant dans un potentiel statique V(r).
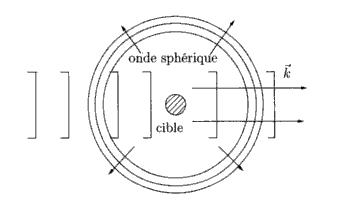
De manière analogue à la diffusion de la lumière par un atome, la fonction d´onde φ décrivant la diffusion de la particule fictive est la somme d´une onde plane et d´une onde sphérique .
r très grand (par rapport à la distance caractéristique du problème) est :
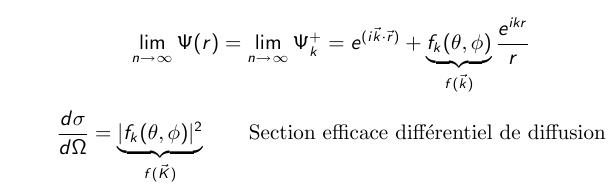
Une méthode permettant de déterminer le coefficient de diffusion est décrite par le schéma suivant :

Un flux de particules de masse et d'impulsion connues ( F=nivi où ni est la densité et vi leur vitesse) est envoyé sur des particules cible de densité connue nc dont on souhaite connaître le coefficient de diffusion σ.
A l´aide d´un détecteur d´angle solide ΔΩ(ΔΩ → 0, on le considérera égal à dω) on peut enregistrer le nombre de particules nd dévié par la cible, on en déduit le différentiel du coefficient de diffusion sur l´angle solide ΔΩ
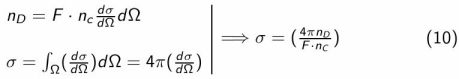
L'équation de Boltzmann se dérive rigouresement du théorème de Louville. Il est possible d'obtenir cette équation plus rapidement( de façon purement formel), en faisant, dans un premier temps l'hypothèse de l'absence de collisions entre les particules. Dans un second temps, l'effet des collisions sera pris en compte.
A l'instant t, le nombre de particules dans l'élément de l'espace des phases drdp centré autour d'une valeur de r,p est f(r,p,t)drdp, où f(r,p,t) est la fonction de distribution des particules dans l'espace des phases. En l'absence de collision, l'écoulement dans l'espace des phases se comporte comme un fluide incomprssible (théorème de Liouville) de sorte qu'a un temps t+dt, les particules de cet élément drdp se retrouvent au point
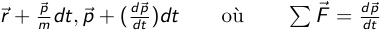 représente les forces extérieures.
représente les forces extérieures.En dévelopant en série de Taylor cette expression au premier ordre, on trouve
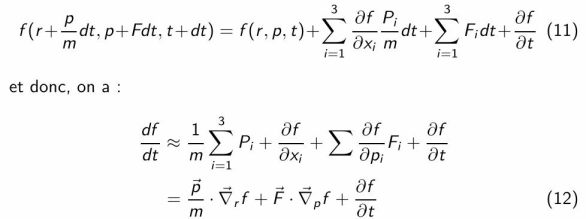
Où
 r et
r et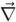 p sont les gradiants dans l'espace des positions et dans l'espace des impulsions.
p sont les gradiants dans l'espace des positions et dans l'espace des impulsions.
En l'absence de collisions, le nombre de particules contenues dans un élément de volume de l'espace des phases est conservé, ainsi df/dt=0, d'où, l'équation de Vlasov (équation de Boltzmann sans le terme de collision):
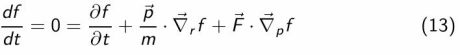
Pour la seconde étape, nous considérerons des collisions binaire.Nous poserons, sans autre justification :
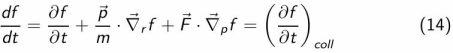
Dans notre expérience, les particules sont des fermions, deux fermions qui subissent un potentiel Vext(r) sont décrits par les fonctions de distributions f↑↓(r,p,t) qui obéissent à l'équation de Bolztmann :
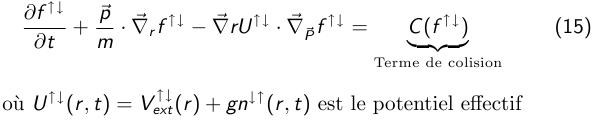
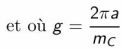
Les collisions entre deux fermions de même spins sont négligées à notre échelle de température.
L'état stationnnaire du nuage est donné par la solution stationnaire de l'équation de Boltzmann (15), qui est la distribution de Fermi-Dirac :
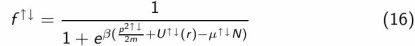
où μ↑↓ est le potentiel chimique qui vérifie la condition de normalisation :
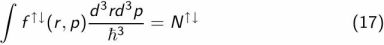
On doit donc trouver μ↑↓ tel qu´il est imposé dans l´équation (17).
Dans cette partie, nous prendrons en compte les intéractions interparticulaires qui existent dans le gaz fermionique. Alors, nous aurons besoin de quelques notions théoriques pour bien comprendre ce phénomène au sein de notre système quantique.
Notion de longueur de diffusion
Tout comme en physique classique, l'étude d'une collision entre deux particules quantiques de masse m peut être remplacée par celle de la diffusion d'une particule fictive de masse réduite μ=m/2 évoluant dans un potentiel statique. De manière analogue à la diffusion de la lumière par un atome, la fonction d'onde ψ décrivant la diffusion de la particule fictive est la somme d'une onde plane incidente et d'une onde diffusée. A longue distance du point de collision, l'onde diffusée est une onde sphérique ,donc ,pour une particule fictive de quantité de mouvement p= hK avant le choc , l'onde résultante est donnée par:
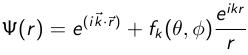
où r et k désignent respectivement la distance au point d'impact et la direction dans laquelle la particule est diffusée. Dans le cas d'une collision élastique où l'énergie cinétique totale des deux particules est conservée, les modules des vecteurs d'ondes sont identiques pour l'onde incidente et l'onde diffusée. L'amplitude de diffusion f est homogène à une longueur et caractérise complètement les propriétés de diffusion. D'après l'interprétation probabiliste de la fonction d'onde, | f (K )|2 est proportionnel à la probabilité d'être diffusée dans la direction K. Bien souvent dans les expériences d'atomes froids, la température des atomes, et donc leur énergie cinétique est tellement basse que l'on peut remplacer f (K ) par sa valeur en K=0 . On pose alors conventionnellement f(0)=-a, où a est appelé longueur de diffusion. a peut être aussi bien positif que négatif et physiquement sa valeur absolue représente la taille effective de l'atome puisqu'en intégrant |f|2 sur toutes les directions de l'espace, on trouve que la section efficace de diffusion élastique à basse énergie vaut simplement 4πa2. Il est notable que, dans la limite de basse énergie, l'amplitude de diffusion ne soit caractérisée que par cette seule longueur de diffusion