Comme indiqué dans la partie programme, le code établit les densités de particule sur chaque case de la grille. Pour afficher ses densités, il nous est obligé d'afficher ses courbes en fixant une quantitée. Dans le compte-rendu, nous avions fixé z, ici, nous fixerons y et observerons les courbes :
- y=5
- y=75
- y=150
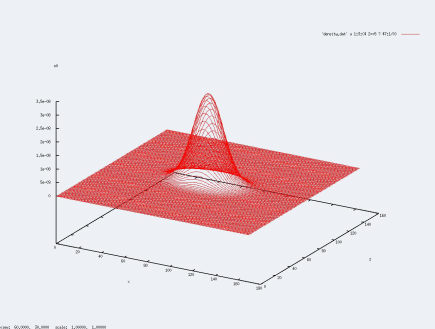
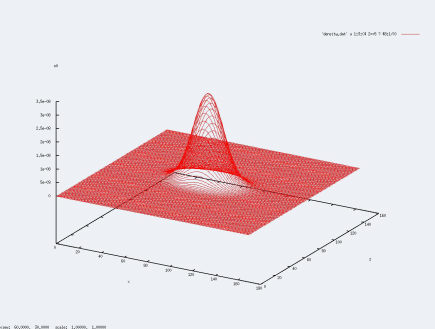
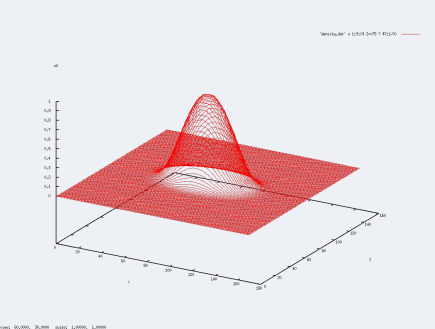
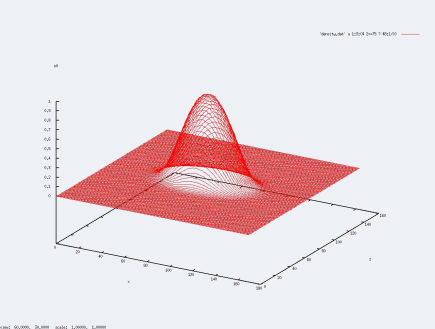
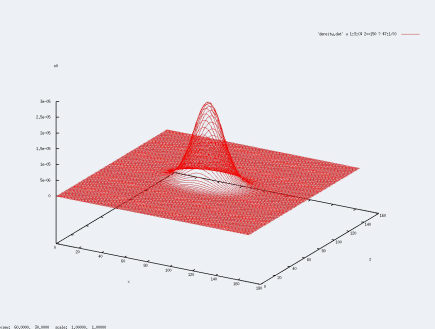
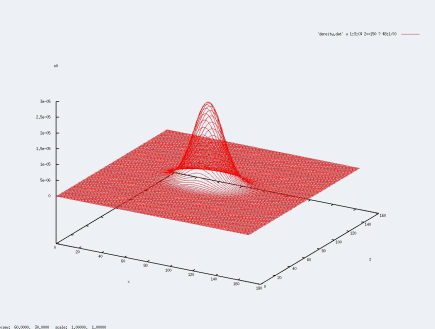
Comme nous l'avons prouvé dans le compte-rendu, dans toutes les simulations que nous effectuerons, la position du centre de masse ne variera que dans la direction z.
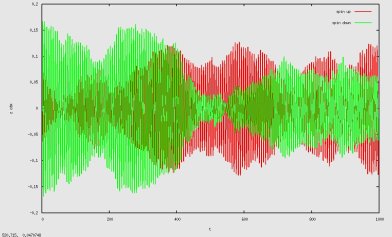
Nous n'afficherons donc que des graphes de l'évolution de la coordonnée du centre de masse en fonction du temps, tout en faisant varier les différents paramètres.
- a : longueur de diffusion
- a fortement répulsif (+1e4)
- a très faible(a=+80) et très attractif(a=-150000)
- cas intermédiaire :a peu négatif a=-500 et -1000
- ω : Fréquence du piège Pour une meilleure visibilité, nous avons choisi de n'augmenter ω que sur le spin up :
- Taille de la grille En augmentant le nombre de cases, on diminue la taille de chaque case ce qui entraîne une augmentation de la précision et donc, une diminution du bruit. Or, le bruit est moins marqué pour un a faible, nous alllons donc comparer les courbes deux a différents :
- a faible
- a élevé
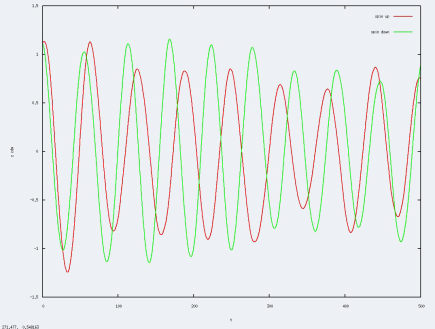
Le résultat correspond bien à la trajectoire de deux pendules reliés par un ressort.
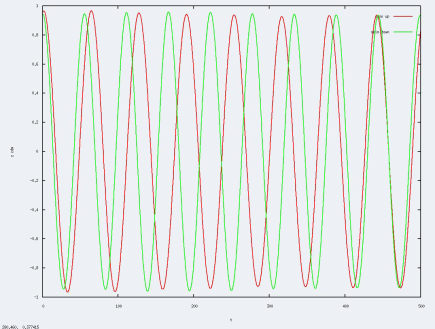
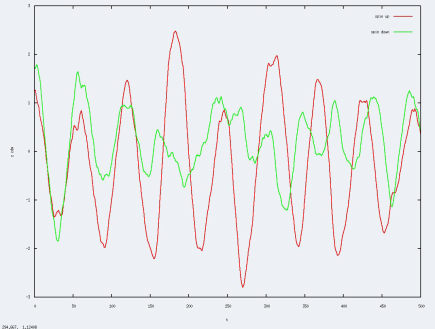
Malgrés le fait que les expériences ne soient pas toujours les même par rapport au compte-rendu, on observe les même types de résultats : pour un a faible, quasiment aucune intéractions ( dans le compte-rendu a=-100, avec les même courbes trouvées), et pour un a très négatif ( les nuages s'attirent très fortement), nous observons bien l'attraction des deux nuages.Cependant, les résultats, pour un a très élevé sont entachés de beaucoup de bruit, nous étudierons donc l'influence de la taille de la grille sur ce bruit.
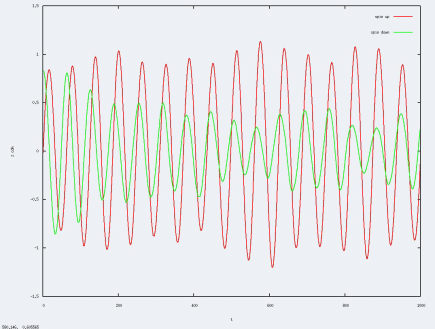
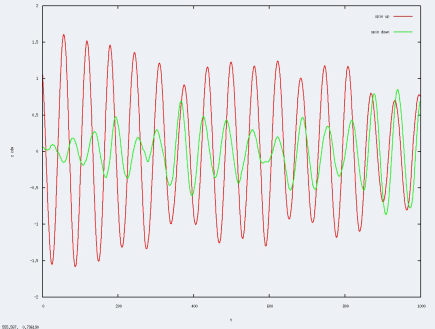
Les résultats collent aux prévisions : on retrouve un comportement hybride entre les extrêmes: les nuages mettent plus de temps à se mettre en phase et gardent une certaine indépendance.
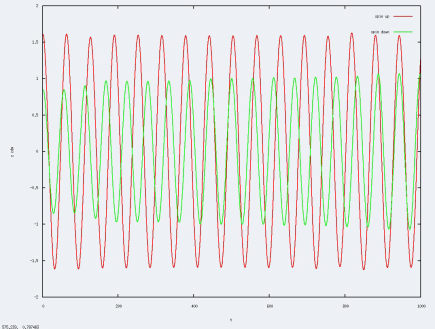
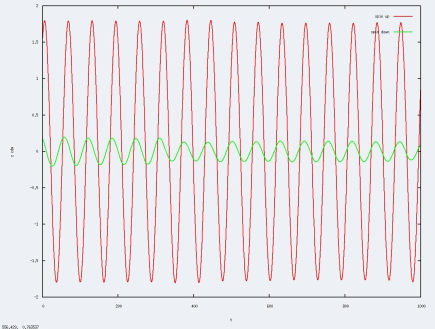
On a bien la longueur caractéristique( amplitude du graphe) inversement proportionnel à la fréquence, comme prévu par l'adimensionalisation du système.


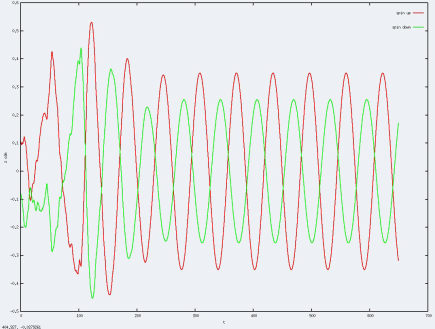
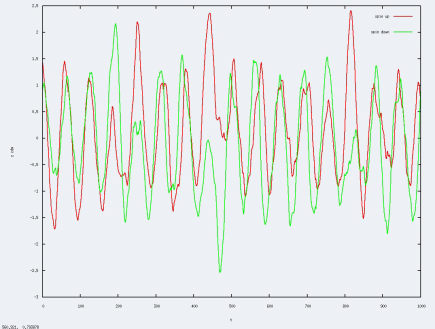
On constate que pour un a faible, il n'y pas de grande différence au niveau du bruit alors que pour a élevé, l'augmentation de la précision sur la grille est très marquée. Si une augmentation de la précision doit être réalisé ce serait pour un a très élevé, si on a le temps : la simulation prend énormément plus de temps en augmentant la précision.