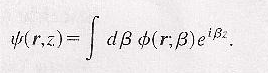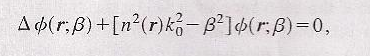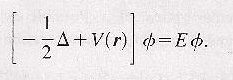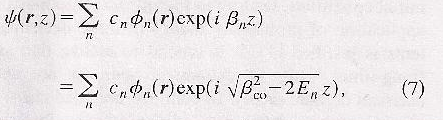| Accueil |
|
PLAN
|
A-FIBRES UTILISÉES :
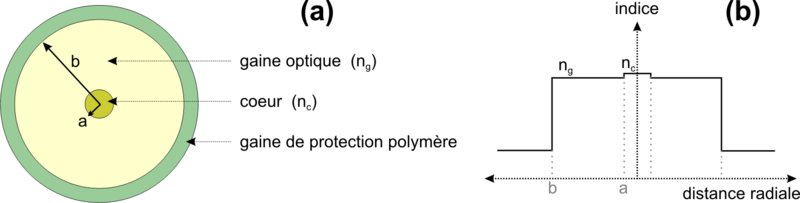
Coupe d'une fibre classique à saut d'indice (a) et répartition radiale de l'indice (b)
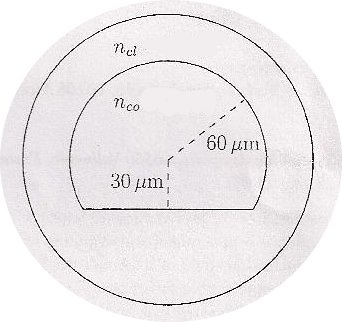
Coupe d'une fibre chaotique à saut d'indice
B-THÉORIE DE LA PROPAGATION ET ANALOGIE QUANTIQUE
Les fibres peuvent être considérées comme des filtres de mode pour le laser. A ce titre on peut comparer les modes guidés par la fibre aux états liés d'une particule quantique, représentée par sa fonction d'onde, dans un puits de potentiel. En mécanique quantique l'état de la particule est une superposition des états liés du puits de potentiel sélectionnés en fonction de l'énergie de la particule, en optique, l'image sur l'écran en sortie de fibre est une superposition des modes guidés par la fibre sélectionner en fonction de l'angle d'entré du laser dans la fibre. Montrons cette analogie
Soit l'équation de stationnaire d'Helmholtz en 3D où : -z représente la position le long de l'axe de la fibre , -r la position dans le plan transverse, -n l'indice du milieu supposé invariant par translation -Δ est le laplacien transverse -k0=2π/λ, λ la longueur d'onde dans le vide de la source
Maintenant si on pose
(1) devient :
Si on note ncl l'indice de la gaine et nco l'indice du coeur, pour
l'équation (3) se résout avec des valeurs discrètes de β qu'on nommera βn. Ces βn sont les constantes de propagation des modes guidés
L'équation (3) peut être alors écrite sous la forme
en posant : -V(r)= ((βco)²-n²(r)(k0)²)/2 , n ne prenant que deux valeurs V(r) ressemble à un puits de potentiel -E= ((βco)²- β²)/2
on a alors l'analogie avec l'équation de Schrödinger stationnaire pour un puits de potentiel
Les valeurs propres d'un tel Hamiltonien sont discrètes, E prend des valeurs discrètes En liées aux βn par
Ainsi la solution de l'équation (1) est
la valeur des coefficients devant l'exponentielle dépend de l'angle entre le rayon lumineux et l'axe de la fibre. (les équations et les notations utilisées dans ce paragraphe sont extraits de l'article Speckle statistics in a chaotic multimode fiber, de V.Doya, O.Legrand et F.Mortessagne)
C - VISUALISATION DES MODES ET CONSIDÉRATIONS EXPÉRIMENTALES :
L'interféromètre de Michelson construit est réglé est caractérisé par les expériences précédentes. Nous pouvons à présent introduire les fibres, pour l'instant non chaotiques à symétrie cylindrique, sur les bras retour des rétroréflecteurs :
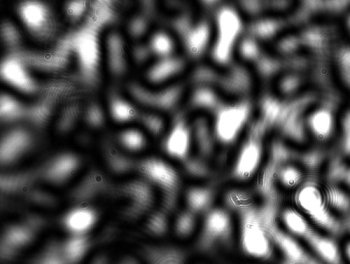
En cachant un bras et en faisant passer le faisceau par une fibre sur l'autre, nous obtenons la figure corrrespondant aux modes séléctionnés par la fibre :
Image reçue par la caméra à la sortie d'une fibre
Cependant avant de faire interférer les faisceaux issus des deux fibres, nous devons nous assurer que les fibres optiques sont parfaitement alignés avec le faisceau laser et fournissent la même figure lumineuse en sortie. Ceci nécessite de pouvoir effectuer la translation habituelle, plus une rotation autour de l'axe optique. Nous devons donc faire construire de nouveaux supports qui répondent à ces conditions.
|