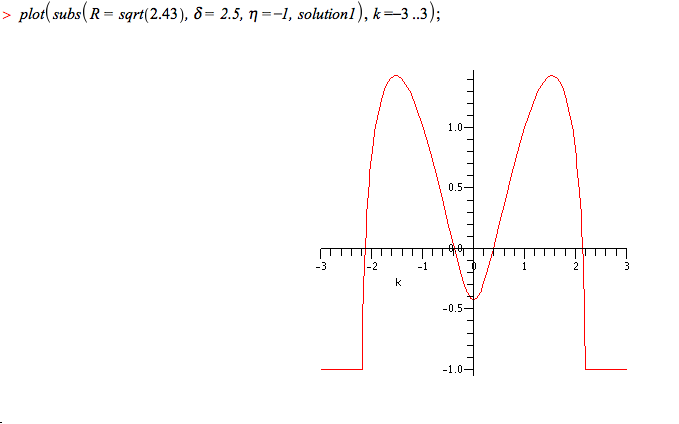Dans le cas de la solution générale, on ne peut pas résoudre l’équation différentielle par l’analyse. Nous sommes donc passer par une résolution à l’aide du logiciel Maple.
Sur le logiciel, on fixe les valeurs de delta et S.
Si delta² > 3, il peut y avoir plusieurs valeurs de E pour un S donné.
Il peut donc y avoir pour un S des valeurs de E correspondant à un régime stable et d'autre à un régime instable.
Dans un premier temps, il a fallu identifier ces différentes valeurs.
On commence donc en posant :
F = x + iy et F* = x – iy
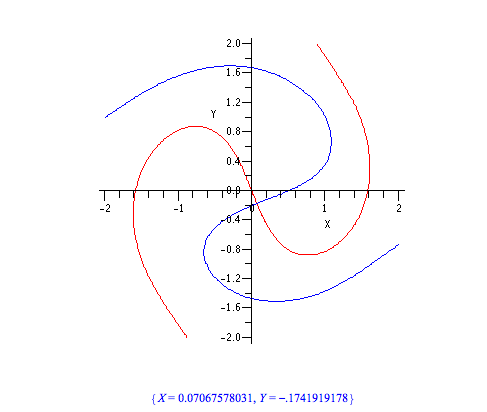
En remplaçant F ou F* dans , on obtient une équation pour la partie réel (rouge ) et une autre pour la partie imaginaire. ( bleu )
Exemple pour un S n'ayant qu'une valeur de E associée.
Exemple pour un S ayant plusieurs valeurs de E associées.
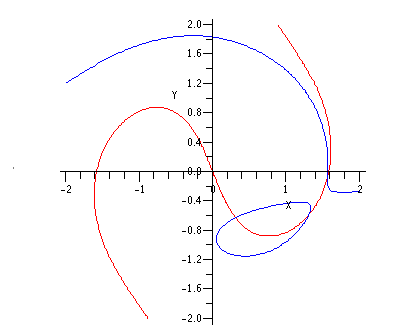
Le tracé des solutions a ces deux équations nous donne au point d'intersection des courbes les valeurs de E correspondantes.
Nous avons juste appliquer la méthode de Newton pour que le programme nous renvois les solutions.
Une fois chaque valeur de E identifiée, on peut commencer l'étude de stabilité locale.
Le principe est le suivant :
Si le système se trouve dans une position d'équilibre instable, une perturbation ɛ le fera diverger de cette position. Si la position d'équilibre est stable, une perturbation ɛ ne changera pas la position.
Pour cela, on passe en séries Fourrier en posant :
F = S + ɛEexp(i*k*z) et F*= S +ɛE*exp(-i*k*z)
avec k nombre d'onde.
On introduit ensuite ces deux équations dans l'équation initiale pour obtenir un système d'équation que l'on peut aisément résoudre grâce à Maple. Le déterminant de la matrice associée à ce système nous donne par la suite une équation d'onde dépendant de k. L'étude de cette équation nous a permit d'établir que les résultats suivant ) :
De X = 0 à X= X1 (1) , l'onde est stable pour tout k.
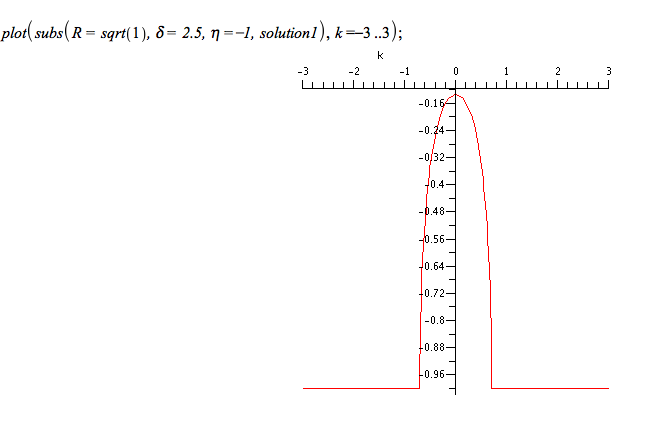
De X = X1 à X = X2 (2), l'onde est instable pour tout k.
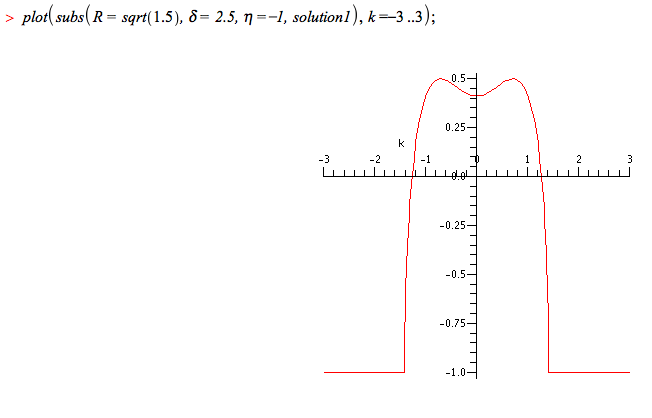
De X = X2 à X divergeant vers l'infini, l'onde est instable jusqu'à une certaine valeur de k où elle se stabilise.