Programmation
Pour l'élaboration de notre programme, nous avons décidé de choisir le language Python, en effet, Python dispose d'une interface graphique permettant d'interférer directement avec les données du programme. Pour un système où les propriétés physiques ont sans cesse besoin d'être ajustées, l'interface graphique est indispensable.
Dans cette partie numérique, nous traiterons uniquement les résultats sans feedback.
Pour le neurone optique, nous avons eu besoin de résoudre les équations de Maxwell-Bloch grâce à la méthode de Runge-Kutta d'ordre 4.
Les équations de Maxwell-Bloch sont couramment utilisées pour modéliser l'interaction lumière matière et décrire la propagation dun faisceau laser dans un milieu non-linéaire.
Voici les équations de Maxwell-Bloch simplifiées par élimination adiabatique de la polarisation pour les VCSELs (Vertical Cavity Surface Emitting Lasers) :
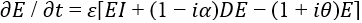
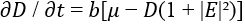
avec E le champ Electrique du laser, ε le taux de décroissance du champ E, EI le champ injecté, α est une constante, θ un paramètre lié au désaccord de cavité, D est la variation de population, b le taux de décroissance de D et μ un paramètre lié au courant de pompage.
Tout d'abord, il nous faut trouver un point d'équilibre instable pour lequel une perturbation de la phase du champ injecté (soit positive, soit négative) va pouvoir générer une réponse excitable. Pour ce faire, nous devons donc nous rapprocher des paramètres physiques qui nous permettront de visualiser au mieux les réponses du système. Il suffit pour cela de trouver une valeur du désaccord de cavité qui fait que le système passe tout juste d'un état instable à un état stable. On passe alors respectivement d'une phase dite "décrochée" à une phase dite "accrochée". On parle de bifurcation. Graphes 1
Une fois les paramètres du sytème trouvés, il nous faut trouver le seuil d'excitabilité en ajoutant une perturbation dans la phase du champ injecté à l'aide des touches du clavier auquelles nous aurons associé auparavant différentes valeurs de perturbation. Graphes 2Par exemple, pour une perturbation de 34.6 degrès, nous n'observons aucun changement sur le graphe de la différence de phase (juste une très légère augmentation, puis stabilisation). Pour une perturbation de 36 degrès, nous observons une impulsion, preuve d'une réponse excitable. Le seuil d'excitabilité sera donc compris entre ces deux amplitudes de perturbation de la phase du champ injecté.
On montre aussi l'espace des phases dans le programme afin de vérifier, chaque fois que nous observons un saut de phase (passage de -π à π et vice versa), que nous obtenons bien une réponse excitable. De plus, nous savons que la projection de l'espace des phases (partie imaginaire du champ E en fonction de sa partie réelle) observée lors d'une réponse excitable représente une bifurcation noeud-col, qui est une bifurcation permettant un caractère excitable à un système.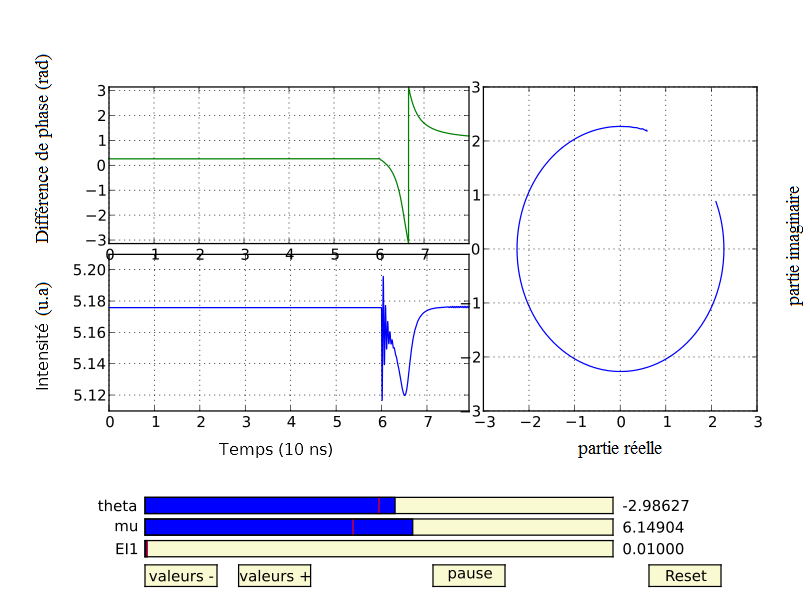
Fig 7. : espace des phases (droite) associée à une réponse excitable (gauche)
Une fois les paramètres physiques trouvés, ainsi que les valeurs de perturbation nécessaires pour mettre en évidence l'excitabilité, nous pouvons vérifier toutes les caractéristiques de cette dernière. En effet, nous vérifions qu'aucune amplitude de perturbation en dessous de la valeur seuil ne permet de bifurcation, et nous observons l'influence de l'amplitude de la perturbation, sur l'intensité et la différence de phase, lorsque la valeur de celle-ci est au-delà de la valeur seuil.
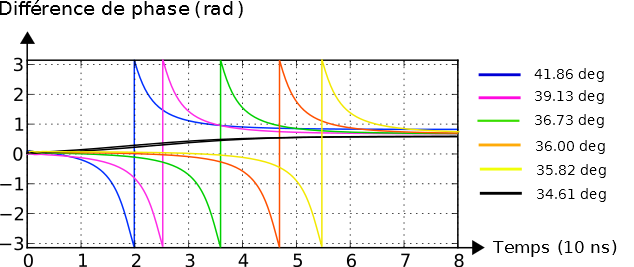
Fig 8. : différences de phase en fonction du temps pour différentes amplitudes de perturbation
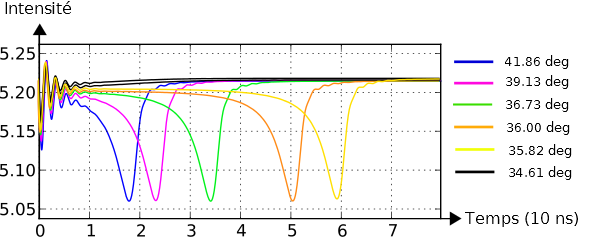
Fig 9. : "modèle de Hodgkin & Huxley" intensités en fonction du temps pour différentes amplitudes de perturbation
A la vue des deux graphes précédents, au dessus de la valeur seuil, plus l'amplitude de la perturbation augmente, plus la réponse excitable arrive rapidement. En effet, notre système numérique représentant un système mathématique presque parfait, sans bruit (autre que le bruit numérique) ni aucune autre source de gêne pour le système. Par conséquent, lorsque l'on se place pile sur le point d'équilibre instable, et que l'on n'applique aucune autre perturbation, le système met un temps infini à perdre cet équilibre et revenir à son état stable. Et, tout comme un pendule simple à tige rigide, si on lui applique en plus une toute petite vitesse initiale, il va perdre son équilibre plus rapidement... Et finalement, la vitesse de perte d'équilibre sera dépendante de l'amplitude de la perturbation.
On retrouve bien là les résultats vus précédemments dans la définition de l'excitabilité, à l'exception du fait que nous observons des impulsions négatives. Ceci est du au fait que les paramètres physiques que
nous avons fixé permettent de déstabiliser notre système en appliquant des perturbations positives dans la phase du champ injecté.



