Notions théoriques
Qu'est-ce qu'un matériau hydrophile/hydrophobe:
Du grecque hudor : hydr(o) eau, phileô aimer, qui aime l’eau. L’eau va s’étaler au maximum sur ce type de surface d’où le mot hydrophile. Pour l’hydrophobie, on part aussi des racines grecques, phobos peur. L’eau essayera d’avoir le moins de contact possible avec ce type de surfaces. Idem pour oléophile/oléophobe en ce qui concerne l’huile.
Qu'est-ce que la tension de surface:
La tension superficielle est l’énergie à une interface. Dans son état naturel, tout objet va tendre vers son énergie minimale (état d’équilibre). Pour tendre vers cette énergie minimale un liquide va soit s’étaler, soit à l’inverse prendre le moins d’espace possible.La conséquence est qu’à l’interface un liquide va prendre la plus petite valeur possible dans un milieu donné. Elle caractérise également la cohésion d’un liquide, puisqu’il faut vaincre les forces de cohésions internes de celui-ci pour accroître cette surface. Mécaniquement, elle s’exprime comme une force s’opposant à un accroissement de surface et rapportée à l’unité de longueur. L’unité utilisée est le N/m
Notions de mouillabilité:
Un liquide est un état condensé : les molécules s’attirent. Les molécules au sein d’un liquide bénéficient d’intéractions attractives avec toutes leurs voisines et sont dans un état « optimal ». Au contraire, à la surface du liquide, elles perdent la moitié des intéractions cohésives et sont dans un état «non optimal». C’est pour cette raison que les liquides vont ajuster leur formes pour exposer le minimum de surface. La mouillabilité est le résultat de la façon dont s’étale un liquide sur une surface. L’énergie de surface d’un solide : γ est l’énergie à fournir pour augmenter la surface d’une unité E.L−²
Paramètre d’étalement [2] : A partir des trois tensions γA, γB,γAB, on détermine le paramètre d’étalement d’un liquide A sur une surface B. S= γB-( γA+ γAB).
Si S › 0, le mouillage est total et le liquide s’étale complètement. Si S ‹ 0, le mouillage est partiel.
La partie suivante est l’étude d’un cas théorique simple pour comprendre comment un matériau peut être hydrophobe.
Le mouillage est un paramètre dans la caractérisation d’une surface bio-inspirée. Il dépend de deux composantes : la composante chimique avec la composition du matériau et la composante physique avec la structuration du matériau. Dans le cadre d’une surface lisse, on peut mesurer l’angle de contact θC d’une goutte d’eau déposée sur cette surface et déterminer si celle-ci est hydrophobe ou non.
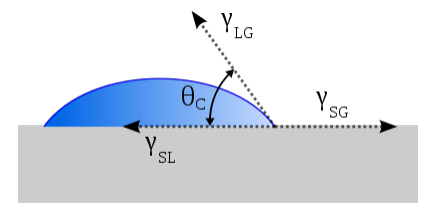
La relation de Young-Dupré [2] permet d’obtenir la valeur de cette angle de contact θC dans une situation de mouillage partiel où le paramètre d’étalement est négatif :
cos θC = (γSG−γSL)/γLG
où γSG, γSL et γLG désignent les tensions superficielles des interfaces solide/gaz, solide/liquide et liquide/gaz. Cette angle doit être mesuré au point triple, c’est-à-dire au point où les trois interfaces se rencontrent.Les résultats obtenus permettent de déterminer le caractère hydrophobe de la surface lisse. Si θC ‹ 90° alors la surface est dite hydrophile, si 90° ‹ θC ‹ 150° la surface est dite hydrophobe et si θC › 150° la surface est dite super-hydrophobe. Les surfaces utilisées par la relation de Young-Dupré sont des surfaces lisses, sans rugosité. La valeur de l’angle de contact ne dépend que de la composition chimique du matériau. Lorsque l’on souhaite étudier des surfaces avec de la rugosité pour savoir si celle-ci influe sur le mouillage, on doit séparer les résultats obtenus en deux cas qui sont décris par les modèles de Wenzel et Cassie-Baxter.
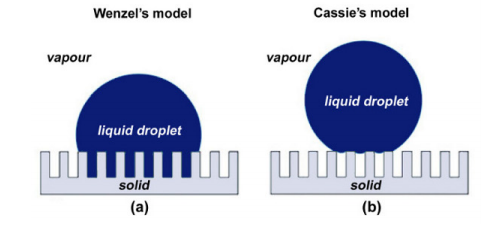
La goutte d’eau déposée sur la surface rugueuse peut être dans deux états différents.
L’état Wenzel [3] montre que la goutte d’eau s’infiltre dans les rugosités de la surface. Cet état peut être décrit par la relation suivante :
cos(θ) = r * cos(θC)
où r est le paramètre de rugosité définit comme le rapport de l’aire de la surface réelle sur celle de la surface apparente. On voit que θ dépend de θC, l’angle de contact pour la surface possédant la même composition chimique que la surface rugueuse, mais sans la rugosité. La valeur de r est supérieure à 1 dans notre cas et égale à 1 s’il n’y a pas de rugosité. Ainsi on observe deux comportements différents pour des valeurs de θC. Si θC ‹ 90° c’est-à-dire si la surface est hydrophile sans la rugosité, alors on aura θ ‹ θC. La propriété hydrophile du matériau est accentuée par la rugosité. A l’inverse, si θC > 90° c’est-à-dire si la surface est hydrophobe sans la rugosité, alors on aura θ > θC et le caractère hydrophobe sera accentué par la rugosité. L’état Cassie-Baxter [3] affirme que la goutte d’eau reste au sommet de la rugosité de la surface. Il s’agit alors d’une surface composite, avec deux milieux différents. Dans le cas du schéma (b), la surface est composée du matériau et de l’air présent dans les rugosités sous la goutte. L’angle de contact θ mesuré est en général supérieur à l’angle de contact du model de Wenzel, car la goutte garde au maximum sa forme sphérique. L’équation décrivant l’état Cassie-Baxter [3] est la suivante :cos θ = φ1 * cos θ1 + φ2 * cos θ2
Avec θ1 l’angle de contact du substrat 1 occupé par une surface φ1 et θ2 l’angle de contact du substrat 2 occupé par une surface φ2. Dans le cas de créneaux analogues comme montré sur le schéma (b), la somme de φ1 et φ2 vaut 1. De plus l’un des milieux étant l’air, l’angle de contact associé à ce milieu vaut 180°. Son cosinus vaut donc -1. On peut simplifier :cos θ = −1 + φS * (cos θC + 1)
Où φS est la fraction de surface occupée par le matériau. La condition qui permet de determiner si la goutte d’eau sera dans l’état Wenzel ou Cassie-Baxter est la suivante :cos(θC) > (1 − φS)/(r − φS) = cos(θF).
Lorsque θC ‹ θF la goutte d’eau imprègne la texture et se trouve dans l’état Wenzel où elle est le plus stable. A l’inverse si θC > θF, alors l’état le plus stable est celui de Cassie-Baxter. Ces deux modèles permettent ainsi de modéliser l’angle de contact apparent θ pris par un fluide sur une surface. Dans le cas du modèle de Wenzel, le fluide est sur une surface rugueuse et pénètre dans ses rugosités. Dans le cas du modèle de Cassie-Baxter, le fluide est sur une surface composite. On peut également parler de surfaces composites dans certains cas particuliers. Les fractions de surfaces φ1 et φ2 dépendant de l’angle de contact θC. La ligne de contact s’ajuste localement de manière à vérifier la relation de Young-Dupré. Dans le cas de picots hémisphériques, la ligne de contact s’ajuste entre la base et le sommet des picots :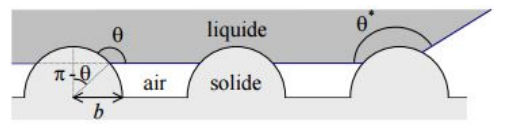
Si φB est la fraction de surface occupée par la base des picots de rayon b, le rapport entre la surface solide recouverte de liquide et la surface projetée est donné par :
φS = (1 + cos θC) * φB
On obtient cette relation en multipliant l’aire d’une calotte recouverte de liquide par le nombre de picots par unité de surface. La fraction de surface occupée par l’air est donnée par :φAir = 1 − φB * sin2 θC
Dans ce cas, l’équation de Cassie-Baxter peut s’écrire :cos θ = −1 + φS * ((cos θC) + 1)²
On voit ainsi que dans le cas de picots hémisphériques, l’angle de contact apparent θ tend encore plus vite vers 180°. Il s’agit alors de surfaces dont la rugosité permet d’obtenir un caractère super-hydrophobe