Menu

Dans cette partie, nous expliquerons comment étudier la pulsation d'une RR Lyrae, grâce à un outil appelé périodogramme.
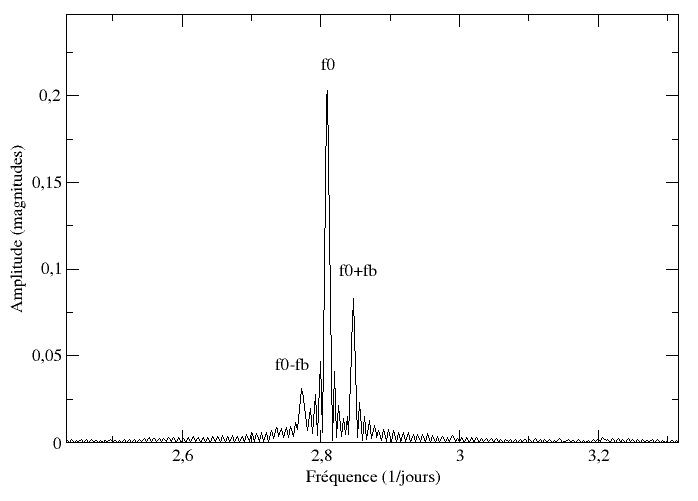
Puis nous verrons comment détecter l'effet Blashko.

Périodogramme

Pour étudier les mécanismes de pulsation des RR Lyrae que nous allons prochainement étudier, nous nous intéressons à l'analyse de fréquences.
En utilisant la décomposition en série de Fourier pour une courbe de lumière, on peut connaître les fréquences de pulsations et leurs amplitudes. On construit alors ce qu'on appelle un périodogramme.

Grâce à la décomposition en série de Fourier, on obtient l'expression de la courbe de lumière sous cette forme:

\( m(t)=A_0 + \sum_{i=1,N} A_i\sin(2 \pi F_i t + \phi_i ) \)

• \( m(t)\) correspond à la magnitude en fonction du temps
• \( A_i \) correspond à l'amplitude de la fréquence \( F_i = i \cdot F_1 \)
• \( \phi_i \) est le décalage de phase de la fréquence \( F_i \) que l'on nomme simplement la phase par abus de langage

On identifie alors chaque fréquence avec l'amplitude et la phase qui lui correspond.

Cas des RRab et RRc

C'est le cas le plus simple. Les RRab pulsent selon la fréquence \( F_1 = f_0 \) du mode fondamental et les RRc pulsent selon le mode de la fréquence \( F_1 = f_1 \) du 1^er harmonique.

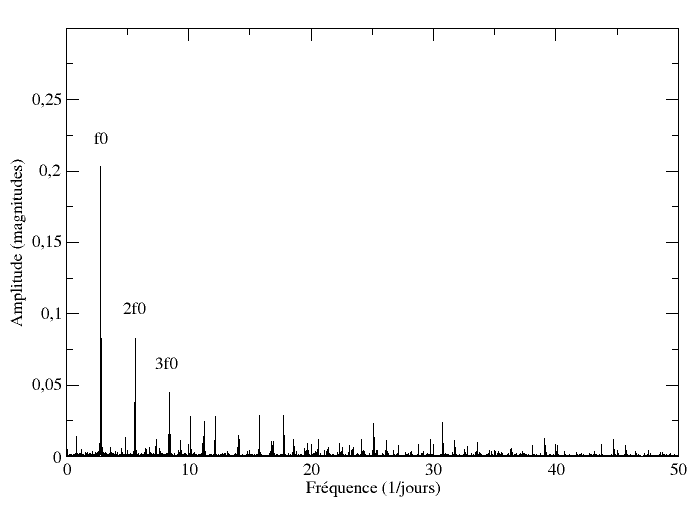
• Pour les RRab, on obtiendra un panel de fréquences de la forme \( n \cdot f_0 \), comme c'est le cas dans la figure 1
• Pour les RRc, on obtiendra un panel de fréquences de la forme \( j \cdot f_1 \)

Remarque: Nous pouvons déterminer si l'étoile pulse selon \(f_0 \) ou \(f_1 \) à partir de modèles théoriques que nous n'avons pas étudié, de par leur importante complexité. Néanmoins, nous pouvons déterminer le type de RR Lyrae que nous étudions grâce à sa courbe de lumière.

Cas des RRd

Ce cas est plus compliqué. En effet, les RRd pulsent selon les fréquences du mode fondamentale et du 1^er harmonique. Nous allons donc détecter à la fois les harmoniques de \( f_0 \), de la forme \( n \cdot f_0 \), et de \( f_1 \), de la forme \( j \cdot f_1 \). De plus, les harmoniques de \( f_0 \) et de \( f_1 \) vont interférer donnant lieu à des couplets de fréquences, qui sont des combinaisons linéaires de la forme \( n \cdot f_0 + j \cdot f_1\). Par exemple, nous pourrons trouver les combinaisons linéaires suivantes : {\( f_0 + 2 \cdot f_1 \)}, {\( 4 \cdot f_0 + 2 \cdot f_1 \)}, {\( 2 \cdot f_0 + f_1 \)}, etc..

Détection de l'effet Blazhko

La présence de structure en multiplet est un indice de la présence de l'effet Blazhko.

En fait, la fréquence blazhko \( f_b \) interfère avec la fréquence fondamentale de l'étoile et ses harmoniques. Il en résultera de nouvelles fréquences de la forme \( n \cdot f_0 \pm k \cdot f_b \) avec \(n\) et \(k\) des entiers naturels. Si l'interférence est constructive, les fréquences résultantes sont de la forme: \( n \cdot f_0 + k \cdot f_b \) ; si l'interférence est destructive, les fréquences résultantes sont de la forme: \( n \cdot f_0 - k \cdot f_b \). À vrai dire, c'est comme ça que l'on a longtemps procédé pour identifier la fréquence Blazhko. Grâce au satellite Corot, qui fait des mesures beaucoup plus précises, nous sommes maintenant en mesure de détecter directement \( f_b \), ainsi que ses 2 premiers harmoniques.

Par exemple:

• Si on détecte les fréquences \(f_0 \), \( f_0 + f_b \) et \( f_0 - f_b \), nous sommes en présence d'une structure en triplet, comme sur la figure 2
• Si on détecte les fréquences \(f_0 \), \( f_0 + f_b \), \( f_0 - f_b \), \( f_0 + 2 \cdot f_b \) et \( f_0 - 2 \cdot f_b \), nous sommes en présence d'une structure en quintuplet

Nous allons utiliser ce savoir-faire pour étudier des données venant du satellite Corot dans la prochaine partie, et ainsi caractériser les étoiles que l'on va étudier.