Menu

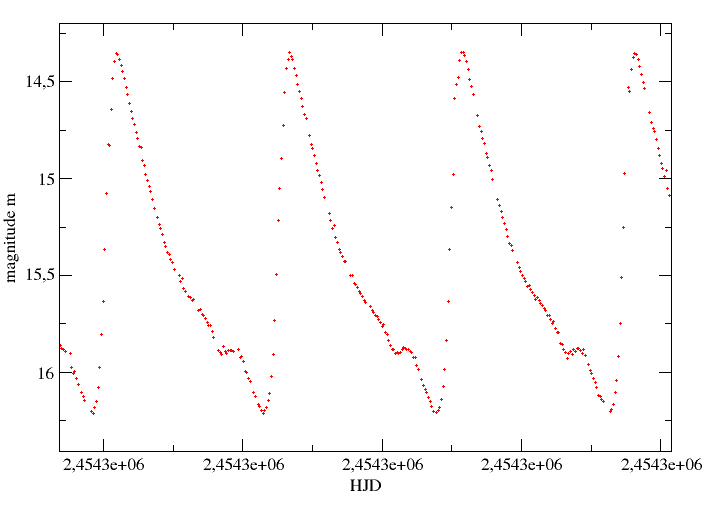
La photométrie est une discipline qui consiste à mesurer la brillance des astres. La mesure de la brillance des étoiles se nomme la photométrie stellaire.
Dans cette partie, nous définirons tout d'abord la magnitude, qui caractérise la brillance des astres, avant d'aborder les notions de "module de distance" et de relation "période-luminosité", qui nous permettrons de déterminer la distance à laquelle on se trouve d'une étoile.
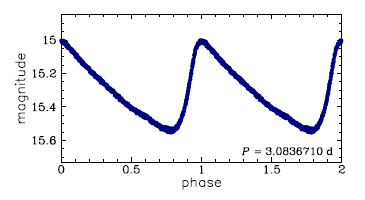
Nous terminerons par la présentation d'un outil utile à la photométrie stellaire, appelé "courbe de lumière".

La magnitude

C’est une échelle logarithmique (en base 10) des éclats d'étoiles mesurés à l’œil nu ou par nos instruments. Nous définirons l'éclat plus bas. On distingue plusieurs types de magnitude :

La magnitude apparente m

\( m=-2.5 \cdot \log{E} + C \)

• \(m\) n'a pas d'unité.
• \(E\) est l’éclat de l’étoile. C'est la quantité d'énergie que l'on reçoit par unité de surface et par unité de temps. C'est donc un flux lumineux, ou une puissance par unité de surface. \(E\) s'exprime en \(W \cdot d^{-1}\)

  \( E=\frac{L}{4Πd^2} \)

  \(L\) est la luminosité de l’étoile (puissance). \(L\) s'exprime en \(W\).
• La distance \(d\) est exprimé en parsec (\(pc\)) (\(1pc=3,26 \,\mbox{années-lumière}\)). C'est la distance à laquelle on se trouve de l'étoile observée.
• La constance \(C\) dépend de l’étoile que l’on va observer et n'a pas d'unité.

On trouve parfois \(m\) suivi d'un indice. Par exemple, \(m_{V}\) désigne la magnitude apparente dans le visible et \(m_{B}\) dans le bleu. La magnitude apparente ne concerne que la partie visible du spectre lumineux.
On a classé les étoiles selon leur magnitude apparente pendant près de 16 siècles. Hipparque, en 150 av J.C, a rédigé un catalogue où étaient classées un peu plus de 1000 étoiles selon leur magnitude apparente.

Contrairement aux Grecs anciens, nous savons que les étoiles ne se trouvent pas toutes à la même distance de la Terre. Selon la distance à laquelle elles se trouvent de nous, elles nous paraissent plus ou moins brillante. En aucun cas nous ne pouvons connaître la "véritable" brillance de ces étoiles en ne considérant que cette donnée. Classer les étoiles seulement grâce à leur magnitude apparente est donc obsolète.

La magnitude bolométrique apparente \(m_{bol}\)

On la nomme bolométrique, car on prend en compte toutes les longueurs d’ondes du rayonnement émis par l’étoile. On utilise la même formule que celle de magnitude apparente, à ceci près qu’il faut prendre en compte toutes les longueurs d’ondes dans l’éclat de l’étoile.

La magnitude absolue \(M\) et le module de distance

C’est la magnitude apparente qu’aurait une étoile si on se plaçait à une distance de 10 parsecs d’elle. \(M\) n'a donc pas d'unité.

\(M=-2.5 \cdot \log{\frac{L}{4\pi \cdot 10pc^2}} + C\)

On la relie à la magnitude apparente par la relation suivante, nommée module de distance :

\(m - M=5\log{d} - 5\)

On remarque que l'on s'est affranchi de la constance \(C\).
Ce qui veut dire que si l'on connait les magnitudes apparentes et absolues d'une étoile, on a la distance qui nous sépare d'elle.

Relation période-luminosité

Pour certaines étoiles variables pulsantes (voir les étoiles variables) dont la période de pulsation est assez régulière, on a la relation "période-luminosité", qui relie la magnitude absolue à la période de pulsation P de l’étoile :

\(M=a \cdot \log{P} + b\)

\(a\) et \(b\) sont des constantes qui sont différentes selon le type d’étoiles variables pulsantes que l’on observe. On les déterminera dans la section suivante.

Détermination des coefficients a et b

Sur la figure 1 ci-dessous, les droites caractérisant la relation magnitude absolue-période des étoiles de type RR Lyrae, W Virginis et Céphéides classiques. En fait, ce sont les seules étoiles qui ont une période de pulsation assez régulière pour qu'on puisse utiliser cette relation.

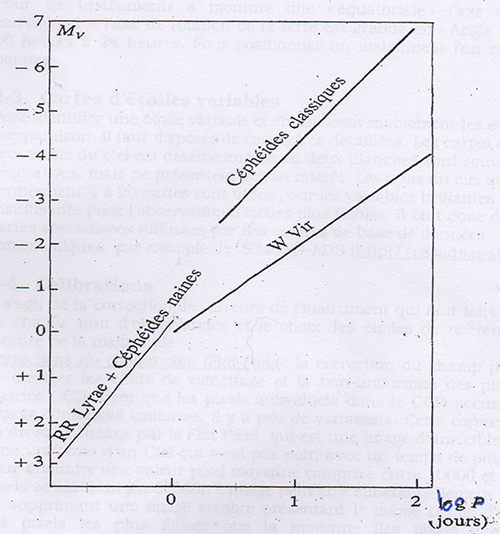
Nous déterminons pour les 3 courbes :

• Leur ordonnée à l'origine qui va nous donner le coefficient \(b\)
• Leur coefficient directeur qui va nous donner le coefficient \(a\), grâce à la relation : \(a=\frac{y_b -y_a}{x_b – x_a}\)

Nous mettons les résultats dans le tableau suivant:

Courbes de lumière

La luminosité de certains types d'étoiles varie en fonction du temps. C'est le cas des étoiles variables, dont nous parlerons dans la page les étoiles variables. On utilise alors un outil qu'on appelle une "courbe de lumière" pour caractériser cette variation de luminosité. À partir d'une courbe de lumière, on peut étudier les mécanismes de pulsations d'une étoile (voir mécanismes de pulsations).

Courbe de lumière et HJD

La courbe suivante représente en ordonnée la magnitude apparente et en abscisse le « Heliocentric Julain day » \(HJD\).

Le \(HJD\) est une unité de temps, dont le jour 0 correspond à l'an -4712 à 12h00, quand le soleil est au zénith, au méridien de Greenwich \(UTC\). Un jour julien dure 24h. Cela facilite la vie des astronomes qui n'ont pas à changer de date pendant une nuit d'observation. On utilise cette unité de temps pour s'affranchir des problèmes liés aux différents calendriers existants, qui ne sont pas toujours pratiques. Il n'y a donc pas à s'encombrer d'années bissextiles, pas de mois qui ont des durées différentes... Pour être précis, il est commode de ne pas négliger les décimales, correspondants aux fractions de jours de HJD. Ces décimales sont importantes dans le calcul de la phase dont on va parler peu après.

Ce système de datation est dérivé du "Julian day" de l'anglais J.F.W. Herschel en 1849, qui l'a lui même adapté de la période julienne de Joseph Juste Scaliger au XVI ^ème siècle. La différence est que le \(HJD\) est voué à tenir compte de l'influence du déplacement de la Terre sur son orbite pendant la durée d'une mesure. Il apporte donc les corrections nécéssaires par rapport au jour julien.
On peut facilement trouver sur internet des convertisseurs de \(HDJ\) en date commune et inversement comme celui-ci : http://www.physics.sfasu.edu/astro/javascript/hjd.html
Il existe d'autres variantes des jours juliens, dont le calendrier commence à une date contemporaine pour ne pas s'encombrer du nombre énorme de jours comptés depuis -4712.

Courbe de lumière et phase

Si on ne dispose pas de site d'observation exceptionnels où la nuit dure 6 mois comme en Antarctique, on ne peut pas observer les étoiles en continu à cause de l'alternance jours-nuits. Si on construit la courbe de lumière d'une étoile, il manque donc des points, correspondants aux instants où l'on était dans l'impossibilité de faire des observations. Néanmoins, au cours d'une autre nuit d'observation, on aurait pu récolter les données manquantes. Pour pallier à ce problème, on fait ce qu'on appelle un "compositage". C'est-à-dire qu'on s'arrange pour avoir toute l'information nécessaire sur une seule période de pulsation en juxtaposant toute nos données. On exprime alors notre courbe de lumière en fonction de sa phase.
La phase \(\phi\) se calcule de cette manière :

\( \phi= \frac{HJD - HJD_{max}}{P} - E(\frac{HJD - HJD_{max}}{P})\)

• \(E\) est la fonction "partie entière". Pour ceux qui ne l'a connaissent pas, c'est une fonction qui permet de prendre la partie entière d'un nombre décimal.
  Ex : \(E(68,2) = 68\)
• \(HJD\) est le HJD auquel on se trouve actuellement.
• \(HJD_{max}\) est le HJD auquel la magnitude est la plus faible (l'éclat est donc maximal).
• \(P\) est période de pulsation de l'étoile.

En calculant la phase, on obtient un chiffre entre 0 et 1.

On peut aussi exprimer la phase sur plusieurs périodes pour avoir une meilleure vue d'ensemble, comme sur la figure 4.

Les notions de photométrie étudiées ici seront utiles à l'étude des étoiles variables. Nous présenterons d'ailleurs ces dernières dans la prochaine partie.