-
PRINCIPES EXPERIMENTAUX
L’exfoliation du graphite en quelques couches de feuillets de graphène dans l’eau est un procédé qui permettrait d’obtenir des concentrations très élevées de feuillets de graphène à basse énergie. Le premier problème est la séparation des feuillets, pour cela, nous utiliserons la cavitation ultrasonore. Le deuxième problème sera l’optimisation de la nature du tensioactif, afin d'empêcher la recombinaison des feuillets. De plus, il faudra s'assurer que les temps caractéristiques de ces deux paramètres soient compatibles. La faible épaisseur des feuillets de graphène nous impose l'utilisation de la spectroscopie Raman.
CAVITATION ULTRASONIQUE

La cavitation s'effectue par la formation de bulles microscopiques par phase de compression ultrasonore, comprimant et augmentant la température des bulles, jusqu'à leur implosion, libérant une grande quantité d'énergie. L’énergie de l’impact (onde de choc), provoquée par l’implosion de la bulle atteint les structures se trouvant à proximité, induisant une interaction mécanique et une dissipation calorifique, que nous avons mesurée en relevant les températures en début et fin de session d'une demi heure. Ti=297.75K, et Tf=303.95K. Nous avons donc déterminé que la chaleur dégagée par la sonde est donnée par la relation suivante: Q = mcv∆T = 4.18.10-3×0.2083×6.2=5.4kJ. On peut maintenant comparer cette valeur avec l’énergie délivrée en théorie par la sonde qui a une puissance de 150W, P∆t = 150 × 1800 = 270kJ. On voit donc qu’il y a énormément de pertes. Ceci est principalement dû à la corrosion par cavitation de la pointe ainsi qu'au vieillissement du matériel, il y a une grande dispersion de l’énergie. Même si cette énergie paraît assez faible, les énergies locales dues à l’implosion des bulles de cavitation sont en revanche assez considérables, la pression peut atteindre 1000 atm [3]. L'énergie potentielle de van der Waals est donnée par [4] : U=-(Agraphite.a)/(12.h) Avec Agraphite, la constante d'Hamaker, a, l'épaisseur d'un feuillet et h, la distance entre deux feuillets. Au niveau du rayon de van der Waals, a=h=0,33nm. Donc : U=-Agraphite/12=-4,70.10-19/12≈-10.kB.T à T=300K. Pour qu'il n'y ait plus d'interaction entre deux feuillets, il faut être supérieur à -1.kB.T. Pour cela il faut que h≥3nm. Regardons maintenant si l'énergie d'une bulle de cavitation est suffisante pour séparer deux feuillets : U=P.V=1000.105x(4/3).π.(100.10-9)3=108.kB.T. P, étant la pression et V, la volume d'une bulle d'un rayon de 100nm. L'énergie nécessaire sera donc suffisante pour l'exfoliation.
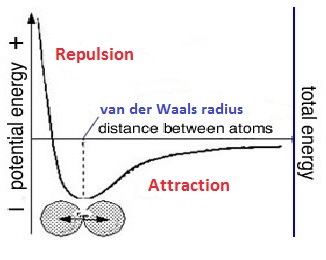 Le problème viendra de la période de compression des ultrasons qui remet en place les feuillets à peine exfoliés en un laps de temps, T = 5,0.10-5s, il nous faudra donc utiliser un écarteur.
Le problème viendra de la période de compression des ultrasons qui remet en place les feuillets à peine exfoliés en un laps de temps, T = 5,0.10-5s, il nous faudra donc utiliser un écarteur.
LE TX-100
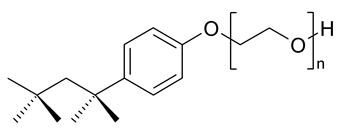
Tout d'abord, pour maintenir en suspension le graphite dans l'eau, il faut utiliser un dispersant. La cavitation permet la séparation des couches, pour isoler celles ci en milieu aqueux, le dispersant doit être tensioactif, afin de rendre les feuillets "solubles" à l'eau. De plus, il faut que ce tensioactif réagisse fortement avec la structure aromatique du feuillet de graphène en interactions π−π pour s'assurer que les feuillets ne se recombineront pas. Le TX-100 remplit toutes ces fonctions : il est dispersant, tensioactif et écarteur (sa partie hydrophobe comporte un cycle benzénique). Cela fait de lui le candidat idéal pour l’exfoliation du graphite. Pour savoir si la molécule de Triton X-100 a le temps de s’insérer entre deux feuillets dans un laps de temps très court, T=5.10-5 s (période d’une oscillation ultrasonore), il faut calculer son coefficient de diffusion. RTX=0,4nm, le rayon de gération de la molécule de TX-100 et T=298K et η=10-3Pa.s. Le coefficient de diffusion brownien est donnée par : D = (kB.T)/(6.π.η.R) D=6,07.10-10m2.s-1. Le rayon d'action du TX-100 est donnée par : a=√(T.D)=174nm Il faut donc que la molécule soit à environ 0.17µm de l’ouverture entre deux feuillets pour pouvoir réagir avec l’un deux. Cela peut sembler assez irréalisable mais il y a, en fait, une grande partie des molécules de Triton X-100 qui réagissent déjà avec les couches externes des morceaux de graphite, c’est d’ailleurs cet effet qui est à l’origine de la dispersion du graphite dans l’eau.
LA SPECTROSCOPIE RAMAN

Pour savoir si l’exfoliation du graphite a bien permis d’obtenir moins d’une dizaine de couches de graphène, il faut acquérir une mesure relative de l’épaisseur des feuillets de graphène par rapport à l’épaisseur des morceaux de graphite originaux. La spectroscopie Raman est une méthode de caractérisation non destructive. Nous avons lu dans certaines études que la raie G aux alentours de 1500cm-1 est plus large pour les monocouches que pour les bicouches et sa position se déplace vers les nombres d’ondes plus élevés [5]. Ce qui nous permettra d'analyser notre progression pendant l'exfoliation.
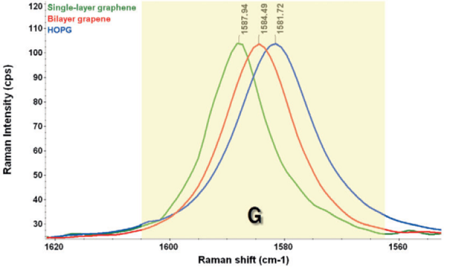
Etant donné que les prévisions théoriques sont concluantes, nous pouvons lancer l'exfoliation. Plus de détails
[3] Hugo Miguel Santos, Carlos Lodeiro, and Jose-Luis Capelo-Martinez,The power of ultrasound in ”Ultrasound in Chemistry :analytical application”,edited by Jose-Luis Capelo-Martinez, (2009), Weinheim. [4] Intermolecular and surfaces forces, J.N. Israelachvili,Academic Press. [5] Joe Hodkiewicz, Characterizing Graphene with Raman Spectroscopy,Thermo Fischer Scientific, Madison, WI, USA(2010), Application Note :51946.