Piégeage
|
Pour cette partie nous allons faire arriver la goutte sur la plaque avec une certaine vitesse. Notre goutte va être piégée par la présence d'un aimant sous la plaque. Celle-ci va osciller autour de sa position d'équilibre. Nous avons mesuré ces oscillations sur la plaque pour l'aimant de hauteur 8.75 mm et de diamètre 5 mm. ObservationsOn peut observer que la goutte se met à osciller autour d'un certain point. Point qui correspond à la position de l'aimant. À partir de ce type film, nous avons obtenu le diagramme spatio-temporel suivant, à l'aide d'imageJ. 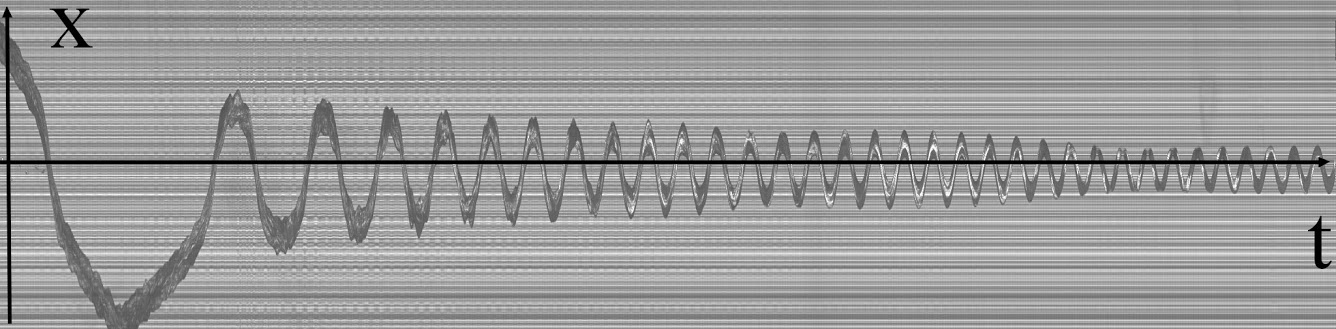 Diagramme spatio-temporel d'une goutte. Sur ce diagramme, nous pouvons suivre le déplacement de la goutte selon l'axe x , ici l'axe de la plaque, en fonction du temps. On peut observer la diminution de l'amplitude des oscillations. Grâce à ce type de diagramme nous pouvons récupérer la pulsation ω. Nous avons répété cette expérience pour différentes hauteurs entre l'aimant et la goutte. 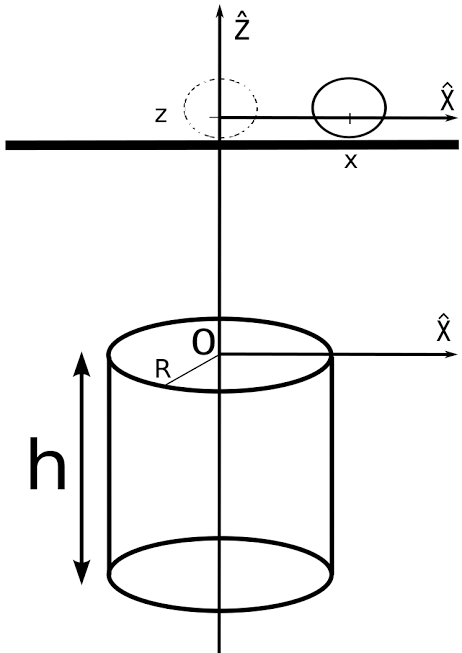 Schéma du montage épérimental à z fixé, les traits en pointillés représentent la postion d'équilibre de la goutte. Analogie mécaniqueOn a pu observer que le comportement de la goutte décrit des oscillations lorsque celle-ci est soumise à un champ magnétique. Nous supposerons que la goutte va décrire une trajectoire horizontale rectiligne sur la plaque. Nous pouvons donc approximer le comportement de la goutte à un système masse-ressort. En effet nous observons la compétition entre l'inertie de la goutte et la force magnétique qui fait ici office de force de rappel. Nous avons donc besoin de calculer le champ magnétique d'un aimant sur la goutte pour trouver l'énergie potentielle magnétique du système. Nous avons déjà vu que l'énergie magnétique volumique est : 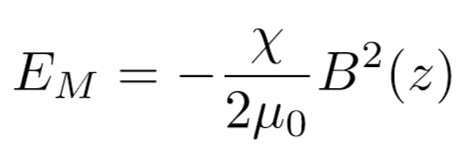 Ici on va se placer à z fixé et s'intéresser au champ selon l'axe de la plaque. Le champ magnétique est maximal au centre de l'aimant, on le note B0 , il est calculé dans Protocole expérimentale et il va décroître en s'éloignant du centre. En faisant une approximation parabolique de l'énergie potentielle magnétique il vient : 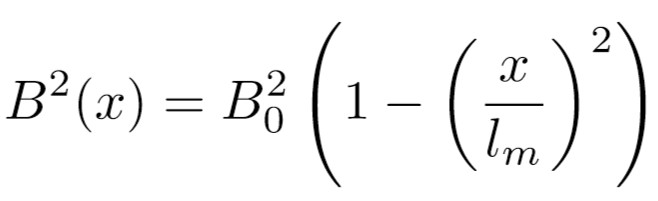 Avec lm une longueur caractéristique de la décroissance du champ suivant x. Au final en faisant l'analogie avec un système masse-ressort la pulsation s'écrit : 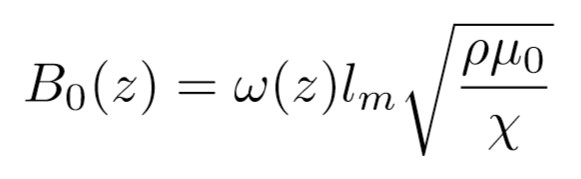 Analyse des résultatsÀ l'aide des pulsations déterminées expérimentalement, nous calculons la valeur du champ B associé. Sur le graphique suivant, nous faisons apparaître également la valeur théorique obtenue à l'aide de l'équation présentée. .png) Grâce à la figure, on peut mettre en évidence que la distance a une influence sur la valeur de la pulsation du système. De plus à l'aide de l'équation précèdente on sait que la pulsation est reliée au champ magnétique. Par conséquent c'est la distance z qui a une influence sur le champ magnétique. Ici nous pouvons nous rendre compte que nos valeurs expérimentales sont en accord avec les valeurs théoriques attendues. |


