Analyse

Branche Turbulente

Pour nos simulations on veut que l'émission du LASER se fasse suivant la branche turbulente (en rouge sur le graphique). Cette branche continu à l'infini quand μ grandit, mais elle disparait en dessous d'une certaine valeur de μ, le LASER retombe alors sur la solution homogene trivial I=0.

Pour trouver cette valeur critique de μ on trace la branche turbulante. Pour cela il faut calculer, pour chaque simulation, la moyenne temporelle des maximums d'intensité de chaque image. C'est à dire pour chaque valeur de t, on cherche le maximum correspondant dans le plan (x,y), puis on moyenne tous ces mamximums par rapport à t.

Dans notre cas on obtient le graphe suivant:



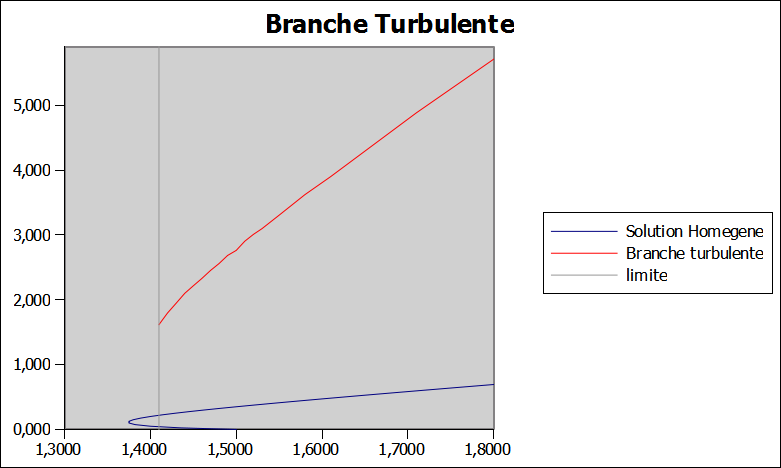
Pour notre plage de paramètre le seuil d'existance de la branche turbulente se situe donc à μ=1,41.
En voyant ce graphique on comprend mieux la nécessité de commencer les simulations avec une grande valeur de μ (ici μ=3,00), on est ainsi assuré que l'émission LASER se fera bien suivant la branche turbulente puisqu'il s'agit de la seule stabilité existant pour cette valeur de μ. Pour des valeurs de μ plus faible (en dessous de μ=1,50), la branche des solitons de cavité (pas représentée ici) et la solution homogène trivial deviennent stable.

Kurtosis

Le Kurtosis est paramètre servant à mesurer l'applatissement d'une distribution de valeurs. Il est définit come le moment centré d'ordre quatre divisé par la variance au carré.

Dans le graphe ci-dessous on représente l'excès de kurtosis, c'est à dire la difference de kurtosis entre notre distribution d'intensité et une distribution Gaussienne classique. Ainsi un excès de kurtosis négatif est caractéristique d'une distribution plus pointue qu'une Gaussienne, tandis qu'une valeur positive indique que la distribution est plus étalée qu'une Gaussienne.



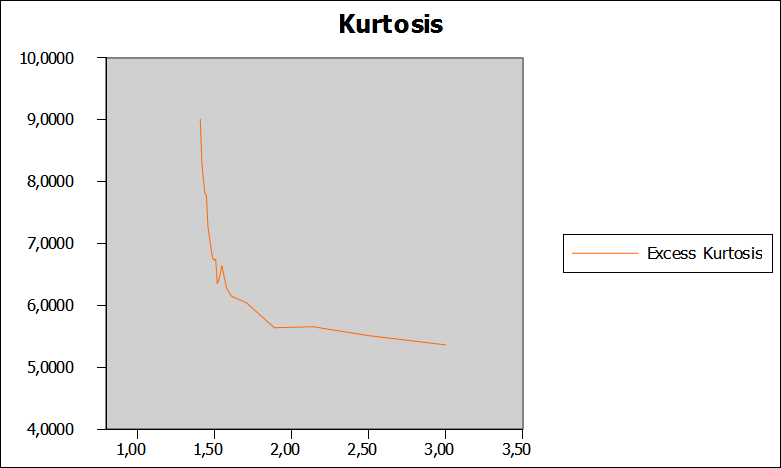
Comme le montre le graphe, l'excès de kurtosis est positif pour toute les simulations, ce qui est normal puisque la présence d'évènements extrêmes donne des distributions d'intensité "à queue lourde" où les fortes intensités sont plus représentées que pour une distribution Gaussienne.

Ce qui est interressant de remarquer ici est la forte augmentation de l'excès de kurtosis lorsque que μ se rapproche de la sa valeur seuil (ici μ=1,41).
Il est important de savoir si cette augmentation de l'excès de kurtosis est lié à une augmentation du nombre d'évènements extrêmes, c'est donc ce que nous allons verifier maintenant.

Critère de Détection des Evenements Extrêmes

Pour sélectionner de manière systématique tous les évnement correspondant à des vagues scélérates, nous avons besoin de critères précis et dont les valeurs dépendent de la simulation étudiée.
Ainsi pour chaque simulation on calculera deux critères différents pour sélectionner les vagues scélérates:
Le premier 2Hs est issu de l'hydrodynamique, il est calculé est faisant deux fois la moyenne du plus haut tiers des maximas d'intensités.
Le second est ‹I›+8σ(I) et vient de l'étude des évènements extrêmes dans les fibres optiques. Contrairement à 2Hs qui dépend uniquement des maximas d'intensité, ce critère utilise toute les valeurs d'intensité de la simulation.



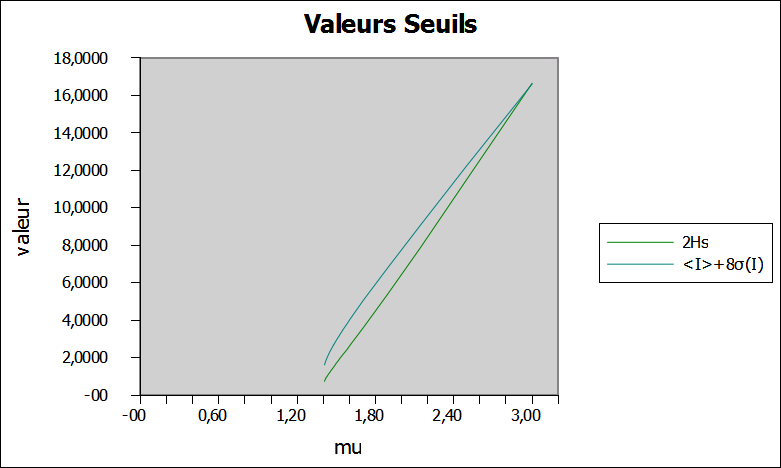
A gauche on voit l'evolution des valeurs des deux critères pour toutes nos simulations.
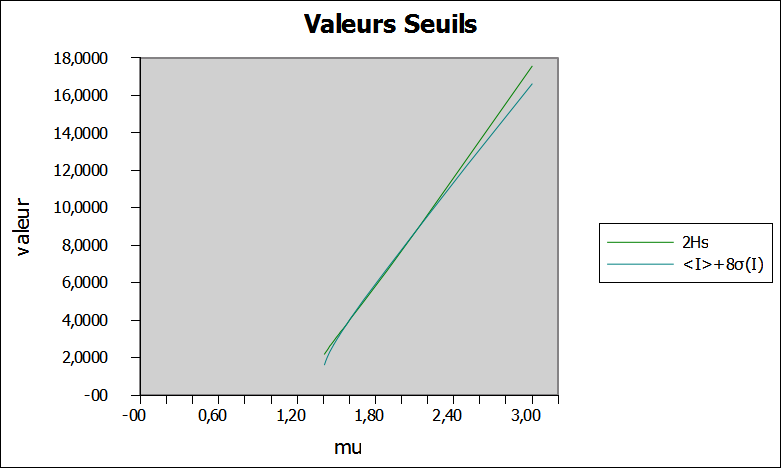
Et à droite on a la même chose mais en ne prenant pas en compte les trés faibles intensités pour le calcule de Hs (tous maxima d'intensité tel que I<0,5 n'est pas pris en compte dans le calcul de 2Hs).

Proportion d'Evenements Extrêmes

Maintenant que l'on a nos critères de sélection pour chaque simulation, on extrait tous les maximas dont la valeur d'intensité est plus grande que 2Hs où ‹I›+8σ(I). Puis nous divisons le nombre d'évènements extrêmes ainsi obtenus par le nombre total de maximas de la simulation pour obtenir le pourcentage de vagues scélérates.

NB: Normalement on ne devrait conserver que le plus grand critère et s'en servir pour selectionner les évènements extrêmes, mais ici le comportement varie beaucoup suivant le critère utilisé donc nous choisissons de représenter les deux.



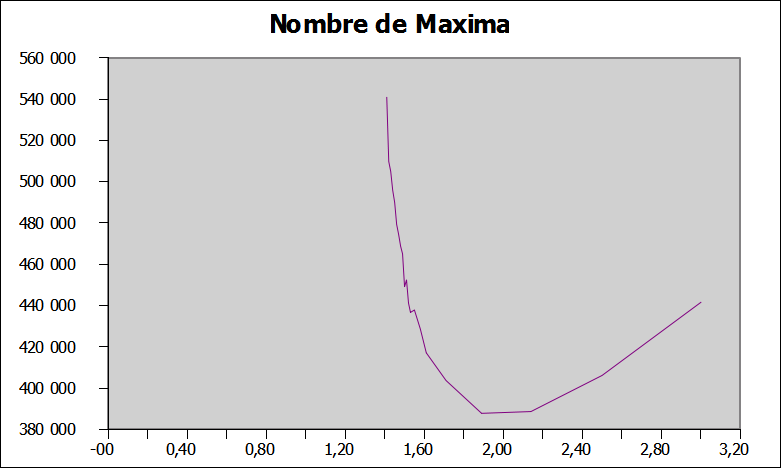
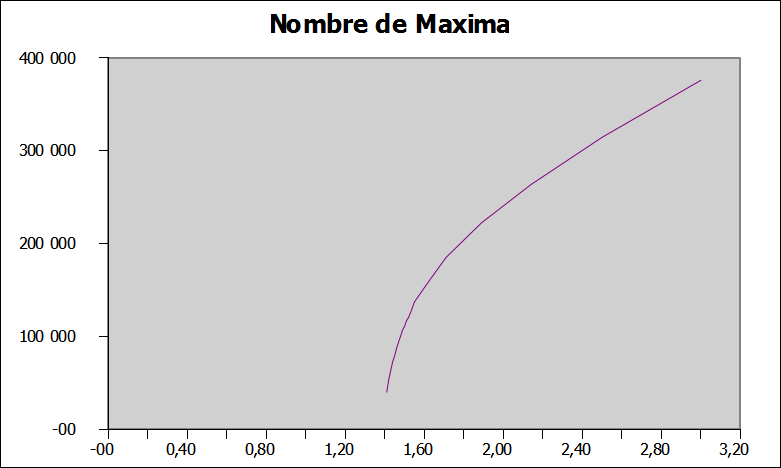
Comme plus haut nous avons deux set de données, à gauche nous conservont toutes les intensités de la simulation, à droite nous ne tenons pas compte des faibles intensités pour le calcul de 2Hs.
Nous représentont l'évolution du nombre de maxima dans ces deux cas, car plus μ diminue, plus un nombre important de maxima sont éliminés avec les petites intensités.

Enfin nous obtenons les graphes suivants represantant l'évolution de la proportion de vagues scélérates en fonction de la valeur de μ utilisée:



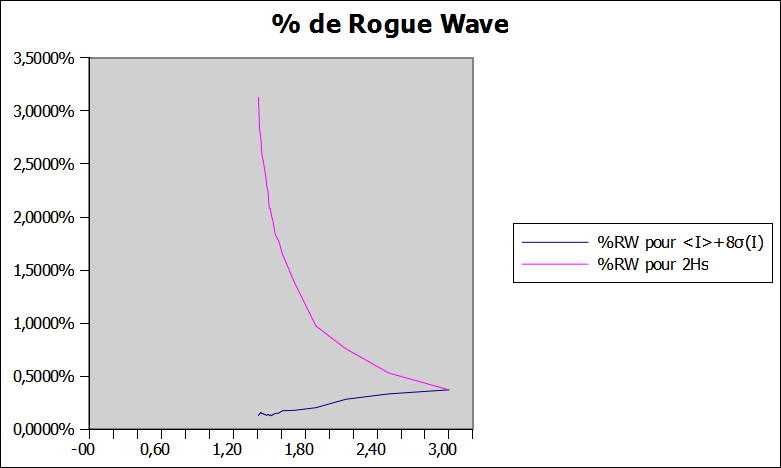
Comme annoncé plus haut, les résultats varient beaucoup.

Pour le graphe de gauche, lorsque l'on considère toutes les intensités, on à des comportements très différents pour les deux critères:
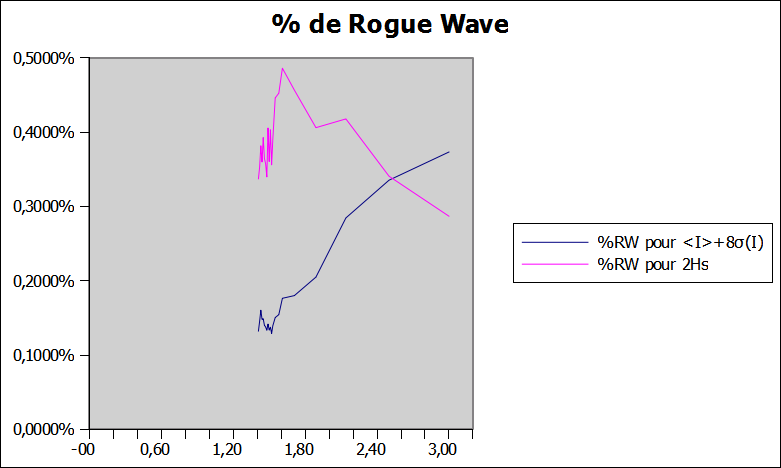
Pour le graphe de droite, en éliminant les petites intensités, les comportements des deux critères sont beaucoup plus proches:

Conclusion

Aprés avoir réalisé toutes nos simulations numériques pour notre set de paramêtres et les avoir analysées statistiquement, il est difficile de conclure quand au comportement de la proportion de vagues scélérates lorsque μ se rapproche de la valeur seuil.
En effet, une partie de nos indicateurs semblent pointer vers une augmentations de leur proportions (distribution à queue lourde, kurtosis et critère hydrodynamique (2Hs)), tandis que l'autre partie de nos indicateur montrent plutôt une baisse de la proportion d'événements extrêmes (critère optique (‹I›+8σ(I)) et analyse en éliminant les faibles intensité).
Pour pouvoir estimer correctement quelle interpretation est la meilleure, il faudrait d'une part déterminer quel critère de sélection est le plus adapté au traitement de nos données, et d'autre part faire un traitement plus fin lors de l'élimination des faibles intensités, en effet avec la méthode actuelle on perd presque 90% des maximas pour les simulations à μ proche du seuil (1,41).



Si le sujet des vagues scélérates vous intéresse et que vous souhaitez en apprendre plus:

Une conference est organisée sur ce sujet, du 15 au 17 Juin 2016 à Nice (laboratoire Dieudonné à Valrose), par Stephane Barland, chercheur à l'INLN et Didier Clamond, mathematicien au laboratoire Dieudonné. Notre encadrante, Mme Tissoni, y donnera une conférence en tant qu'invité.

Pour plus d'information, voici un lien vers le site web de l'événement: The Workshop on Abnormal Wave Events.
Si vous souhaitez y participer, merci de vous inscrire avant le 6 Juin 2016, sur ce lien: Registration form.


[retour haut de page]