Résultats
Profil d'Intensité
Le programme LSArongue.in integre numériquement les équations différentielles (voir onglet Modélisation) décrivant l'émission des VCSEL à absorbant saturable. En sortie on obtient une matrice à trois dimension (x,y et t) dont chaque case contient la valeur d'intensité correspondant à ce point d'espace-temps.Ci-dessous nous visualisons la variation de ces valeurs d'intensité dans le plan (x,y) lorsque t change:
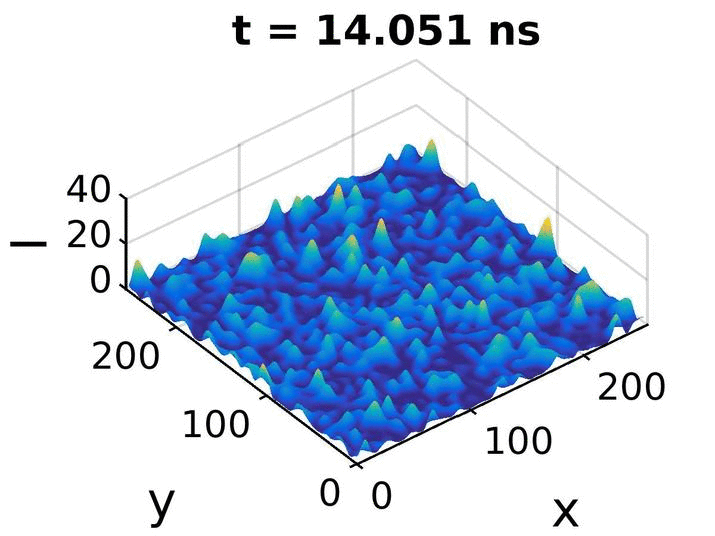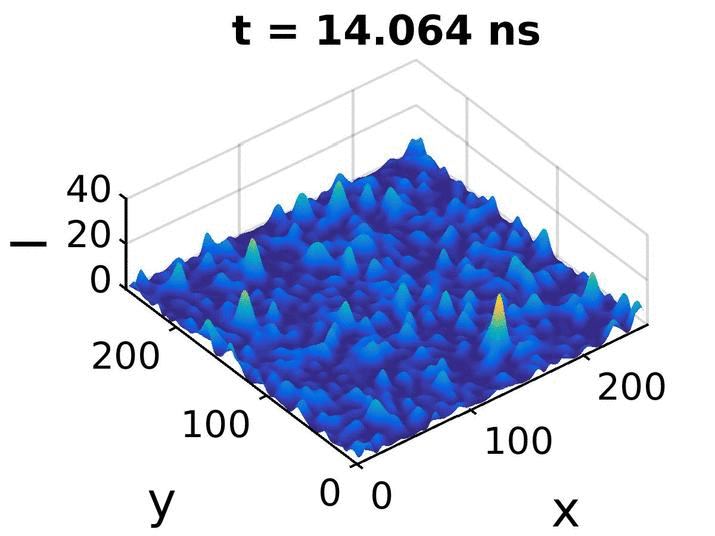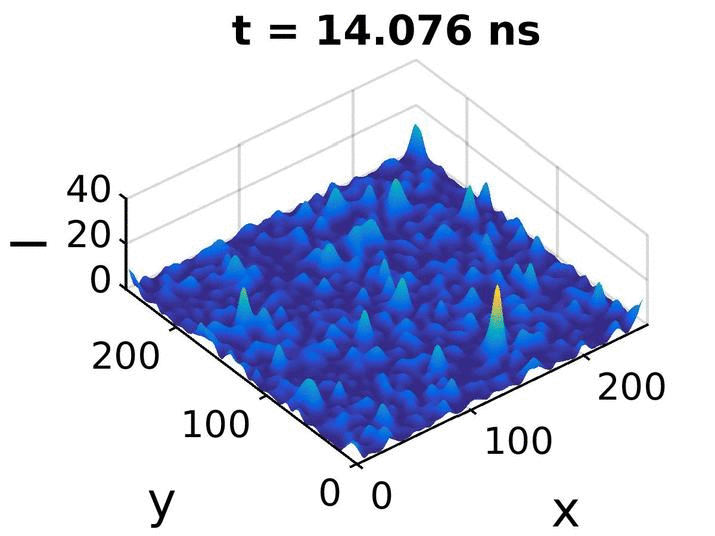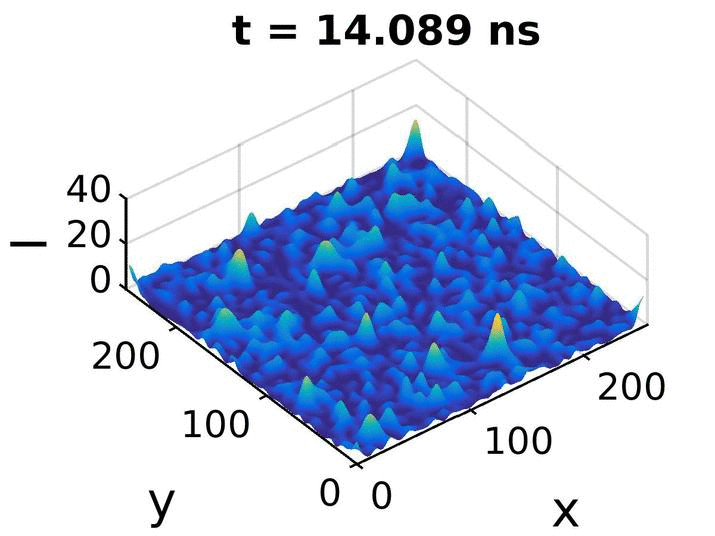
Cette animation est un petit extrait de notre simulation pour μ=3,00 : elle correspond à 40ps autour de l'intensité maximum atteinte par cette simulation.
On voit clairement que les pics d'intensité grandissent dans le temps, atteignent un maxima, puis décroissent.
l'interret de ce projet est d'étudier la distribution des maximas d'intensité.
Il faut donc pouvoir trouver et sélectionner les intensités correspondant à des maximas, non seulement dans l'espace, mais aussi dans le temps. C'est là qu'intervient le programme maxima_contour.m : Il va procéder à une comparaison "en étoile" (dans les trois dimensions) des valeurs d'intensité contenues dans la matrice 3D. Cela veut dire que pour chaque case il va comparer la valeur de l'intensité qu'elle contient avec les valeurs contenu dans les 26 cases adjacentes. Si l'intencité de la case est la plus grande, il s'agit un maxima, sinon il passe à la case suivante et refait le test.
Distribution d'Intensité
Pour comparer nos résultats avec les distributions d'intensité dans les fibres obtenues par les chercheurs travaillant sur ce sujet (ref. 2 et 8) on commence par tracer les densités de probabilités sur toutes les intensités d'une simulation. On obtient les graphes suivants:Pour μ=3,00 :
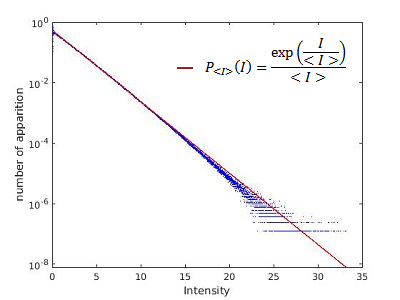
Pour μ=1,50 :
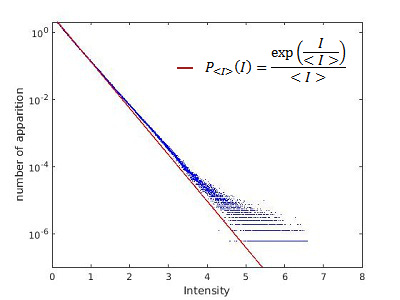
Et pour μ=1,41 :
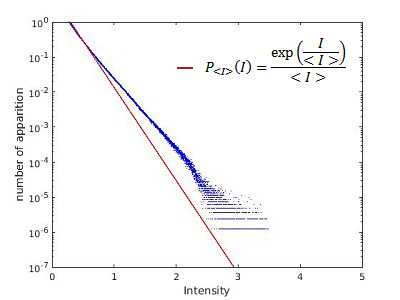
La ligne rouge représente la distribution de probabilité exponentielle, c'est ce que l'on s'attend à observer dans un cas sans événement extrême.
Ici on remarque que la distribution de nos valeurs experimentale à tendance à se déplacer au-dessus de la ligne rouge lorsque la valeur de μ diminue. Cela correspond à un type de distribution statistique appelée "distribution à queue lourde" qui est caractéristique de la présence d'événement extrêmes. De plus il s'agit du même type de graphe que ceux obtenus pour l'étude des évènements extrêmes dans les fibres optiques.
Distribution des Maximas d'Intensité
On passe maintenant au sujet principale de ce projet: la distribution statistique des maximas d'intensité.On regroupe ici trois distributions correspondant à trois simulations différentes. A chaque fois, le graphe de gauche est en échelle normale et celui de droite est en échelle logarithmique.
Pour μ=3,00 :
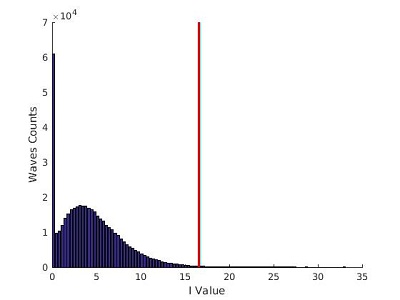
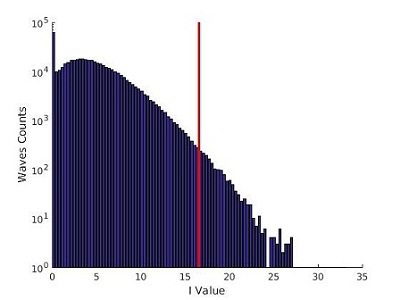
Pour μ=1,50 :
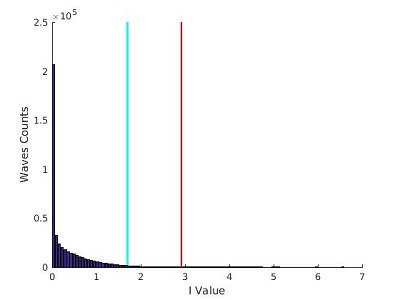
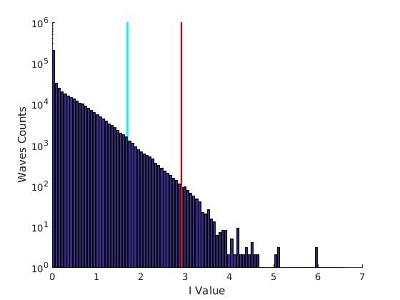
Pour μ=1,41 :
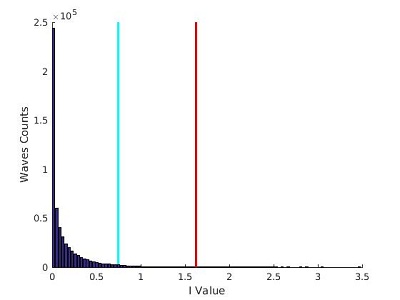
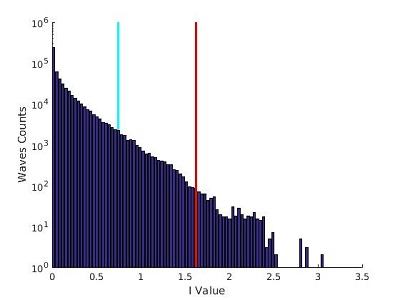
On remarque tout de suite que la forme de la distribution d'intensité change lorsque la valeur de μ diminue: On passe d'une distribution avec un maximum autour de I=5 pour μ=3,00, à une distribution qui décroit rapidement pour μ=1,50 et qui s'incurve encore plus pour μ=1,41.
Les barres bleu et rouge de ces graphes représentes les deux valeurs seuils (2Hs et ‹I›+8σ(I)) qui permettent de selectionner les évènements extrêmes. Nous expliquons dans la partie Analyse comment ces valeurs sont calculées.
[retour haut de page]