Modélisation
Modèle Utilisé
Pour le moment on ne peut pas avoir de « vraie » détection des maximas d’intensité : les capteurs existants ne sont pas encore assez rapides pour permettre de cartographier précisément le profil d’intensité dans l'espace et dans le temps simultanément. Ce modèle repose donc sur une simulation numérique.Il est toutefois important de noter que M. Barbey et son équipe travail sur une thématique similaire à celle de Mme Rimoldi: l'observation d’événements extrême émis par un VCSEL à absorbant saturable dont la dimension transverse est réduite à 1 (au lieu de 2 dans le cas de Mme Rimoldi) (ref. 9) . Leur recherche est aussi bien expérimentale que numérique.
La nouveauté des travaux de Mme Rimoldi viens de deux aspects:
- D'une part nous étudions les evenements extremes dans le plan transverse au laser. Ceci permet d'obtenir un profil d'intencité en trois dimension (x,y,t) au lieu d'une seule dans les fibres optiques (t).
- D'autre part, jusqu'à présent l'étude des distributions d'intensités se faisait sur toute les valeurs d'intensités. Ici nous faisons nos statistiques seulement sur les maxima spatio-temporelles.
LASER à Large Plan Transverse (VCSEL)
C’est un type de diode laser à semi-conducteur émettant la radiation laser perpendiculairement à la surface des miroirs, contrairement aux lasers conventionnels à semi-conducteur émettant par la tranche.Le résonateur (la cavité où à lieu l’amplification) laser est constitué de deux miroirs de Bragg parallèles à la surface du wafer, et, entre eux, d'une région active (l’amplificateur) constituée d'un ou plusieurs puits quantiques permettant la génération du faisceau laser.
Les miroirs de Bragg sont faits de couches alternant haut et bas indices de réfraction. l'épaisseur de chaque couche correspond au quart de la longueur d'onde du laser dans le matériau, permettant ainsi d'obtenir un facteur de réflexion supérieur à 99% (ici des miroirs à haut facteur de réflexion sont nécessaires pour compenser la faible longueur du milieu amplificateur).
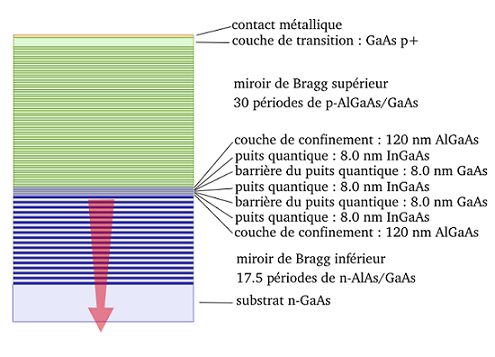
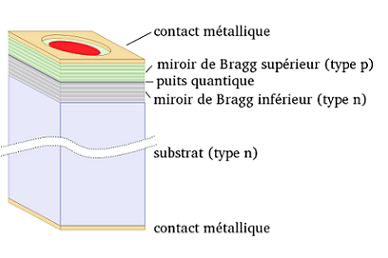 source
source
Les VCSEL ont une grande ouverture de sortie par comparaison avec la plupart des lasers émettant par la tranche, c’est cette propriété qui le rend intéressant dans ce cas. En effet on obtient un profil d’intensité sur une surface (2D), ce qui est plus proche de la réalité physique des vagues sur l’océan que le modèle à 1D de la fibre optique (On peut faire cette approximation car les dimensions suivant la direction z(axe du laser) sont négligeables devant les dimensions dans le plan (x,y).
Laser à Absorbant Saturable
Un LASER classique fonctionne selon le principe suivant : des photons sont créés par émission stimulée dans un milieu amplificateur (ces photons sont tous de même énergie, même polarisation et en phase). La cavité contenant le milieu amplificateur est entourée de deux miroirs partiellement réfléchissant (99%) de sorte que la majeur partie des photons circulant reste piégée dans la cavité et continue le processus d’amplification, tandis que le 1% restant sort de la cavité et donne le faisceau LASER.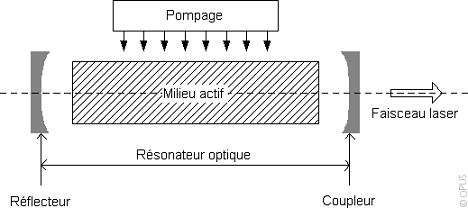
source
Un LASER à absorbant saturable fonctionne suivant un principe très similaire à celui du LASER classique.
La principale différence est le placement, dans la cavité, d’un absorbant saturable (élément optique permettant une absorption qui ralentie lorsque l'intensité de la lumière augmente) ayant la propriété de permettre une absorption à faible puissance. La présence de cet absorbant a pour conséquence de réduire considérablement le gain de l’amplificateur (tant que l'absorbant n'est pas saturé) : le LASER n’émet donc pas ou très peu. Lorsque l’absorbant est saturé, il ne provoque presque plus de perte, donc le gain du LASER devient subitement très important. Cette inversion subite du gain permet l’émission d’un rayonnement de grande intensité (toute l’énergie stockée dans l’amplificateur peut être extraite beaucoup plus efficacement).
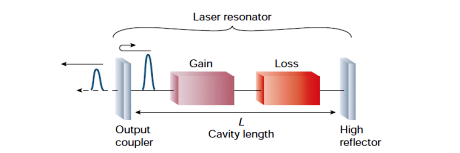
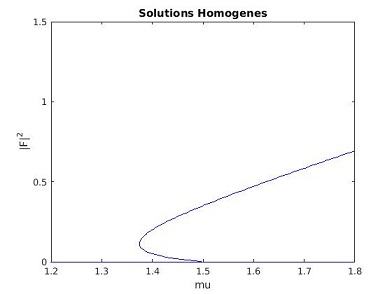
source
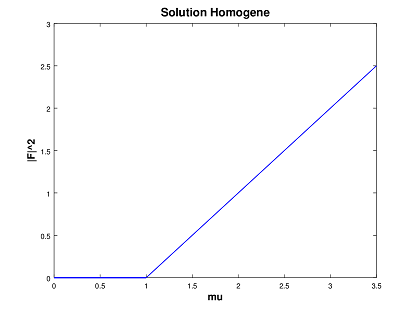
Sur la graphe des solutions homogène pour le LASER à absorbant saturable (ci-dessus, à droite) il est important de noté que la solution homogène triviale (I=0) n'est stable qu'en dessous d'une valeur seuil, et la solution homogène non triviale n'est jamais stable (I›0).
Equations Différentielles
Pour Modéliser un LASER à absorbant saturable où à la fois l'absorbant et l'amplificateur sont des semi-conducteurs, on utilise le set de trois équations différentielles non linéaires suivant (ref. 2):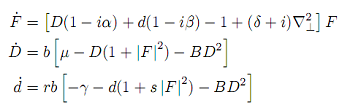
- F est proportionnelle à l’enveloppe lentement variable du champ électrique (complexe).
- D correspond à la proportion du porteur de charge dans l’amplificateur (réel).
- d correspond à la proportion du porteur de charge dans l’absorbant (réel).
Et les Paramètres sont:
- μ est le paramètre de pompe (assimilable à la quantité de courant fourni au laser).
- γ est le paramètre d’absorption (équivalent au paramètre de pompe pour l’amplificateur).
- r correspond au ratio des temps de relaxations de l’amplificateur et de l’absorbant.
- α et β sont des paramètres spécifiques des semi-conducteurs appelés "facteur d'élargissement de raie".
- B coefficient de recombinaison radiative (ici choisi égale à 0).
- b ratio du temps de « libre parcours » des photons par le temps de relaxation de l’absorbant.
- s paramètre de saturation de l’absorbant.
- δ paramètre de diffusion du champ (couplage spatial (diffraction et diffusion) du champ électrique dans le plan (x,y)) .
Par intégration numérique (avec le programme LSArogue1.for) de ces équations on obtient les variation spatio-temporelle des variables F, D et d et on étudie le profil d’intensité dans le plan (x,y).
Programmes Utilisés
Pour réaliser et traiter les simulations nous utilisons les deux programmes suivants:- LSArogue1.for (fortran):
écrit par M. Bache et Mme. Tissoni en 2005, dans le but d’étudier la dynamique spatio-temporelle et la formation de structures transverses dans les systemes laser à semi-conducteur spatialement étendus (VCSEL) (ref. 2).
Ce programme a pour but d’intégrer numériquement les équations différentielles présentées plus haut en fonction des paramètres donnés et de fournir un fichier contenant le profil d'intensité dans l'espace et le temps. - maxima_contour.m (matlab):
écrit par Mme. Rimoldi en 2015, dans le cadre de sa thèse: "Spatio-Temporal extreme events in a LASER with saturable absorber" (ref. 8).
Ce programme lit le fichier d'intensité créer par LSArogue1.for et en extrait tout les maximas dans l'espace et dans le temps. Il renvoi une matrice contenant les coordonnées (x,y,t) des maximas ainsi que le valeur.
[retour haut de page]