Notre démarche
Dans cette partie, nous allons détailler la façon dont nous avons analysé et interprété les fichiers sonores enregistrés dans le précédent stage. Le but étant de mettre en évidence un croisement évité des fréquences et un croisement des largeurs (partie imaginaire) comme prévu dans la partie précédente.
Traitement des données
Nous allons ici analyser de nombreux enregistrements ayant été effectués lors du projet (Chasse au Loup2) réalisé en 2016. Afin de repérer facilement la position du doigt sur le manche du violoncelle, le groupe de projet de 2016 a collé une échelle graduée sur la touche du violoncelle en se plaçant aux alentours de la note du loup. Le zéro de cette échelle est positionné à 30,5 cm du sillet du violoncelle et les graduations sont de 0,25 cm. Typiquement, les séries de données correspondent à des enregistrements sonores pour des positions de doigt sur le manche allant de 2 cm à 7,5 cm sur l’échelle graduée, c’est de cette manière que l’on repérera les fichiers pour toute la suite de l’analyse.

Afin d’effectuer une analyse des données, nous avons défini une fenêtre d'analyse temporelle pour chaque enregistrement. On considère tout d’abord le maximum d’amplitude de chaque fichier et le temps $t_{max}$ correspondant et on normalise ensuite tous les points avec ce maximum. On introduit alors deux paramètres qui servent à délimiter une fenêtre temporelle plus précise : $\delta t$ et $\Delta t$. Le paramètre $\delta t$ permet de définir la position de départ de la fenêtre par rapport à $t_{max}$ c'est-à-dire qu’on a : $t_{0} = t_{max} - \delta t$. On peut alors éliminer la contribution fréquentielle des partiels liés aux transitoires du son. Le paramètre $\Delta t$ sert à délimiter la fin de la fenêtre temporelle : $\Delta t = t_f - t_0$ et permet entre autres de supprimer la contribution du bruit de fond (bruit propre généré par le dispositif d'enregistrement) à l'analyse spectrale. Nous avons alors cherché les valeurs de ces paramètres qui donnent les spectres sonores les plus précis possibles, notamment dans le domaine fréquentiel proche du loup. Ces valeurs des paramètres qui sont propres à chaque fichier de chaque série de données vont également nous servir pour appliquer le procédé de l’Harmonic Inversion.
On s'est intéressé dans un premier temps aux fichiers enregistrés par le groupe de projet précédent le 21 avril 2016. Nous avons alors appliqué la méthode décrite précédemment afin de définir une fenêtre temporelle pour chaque fichier.
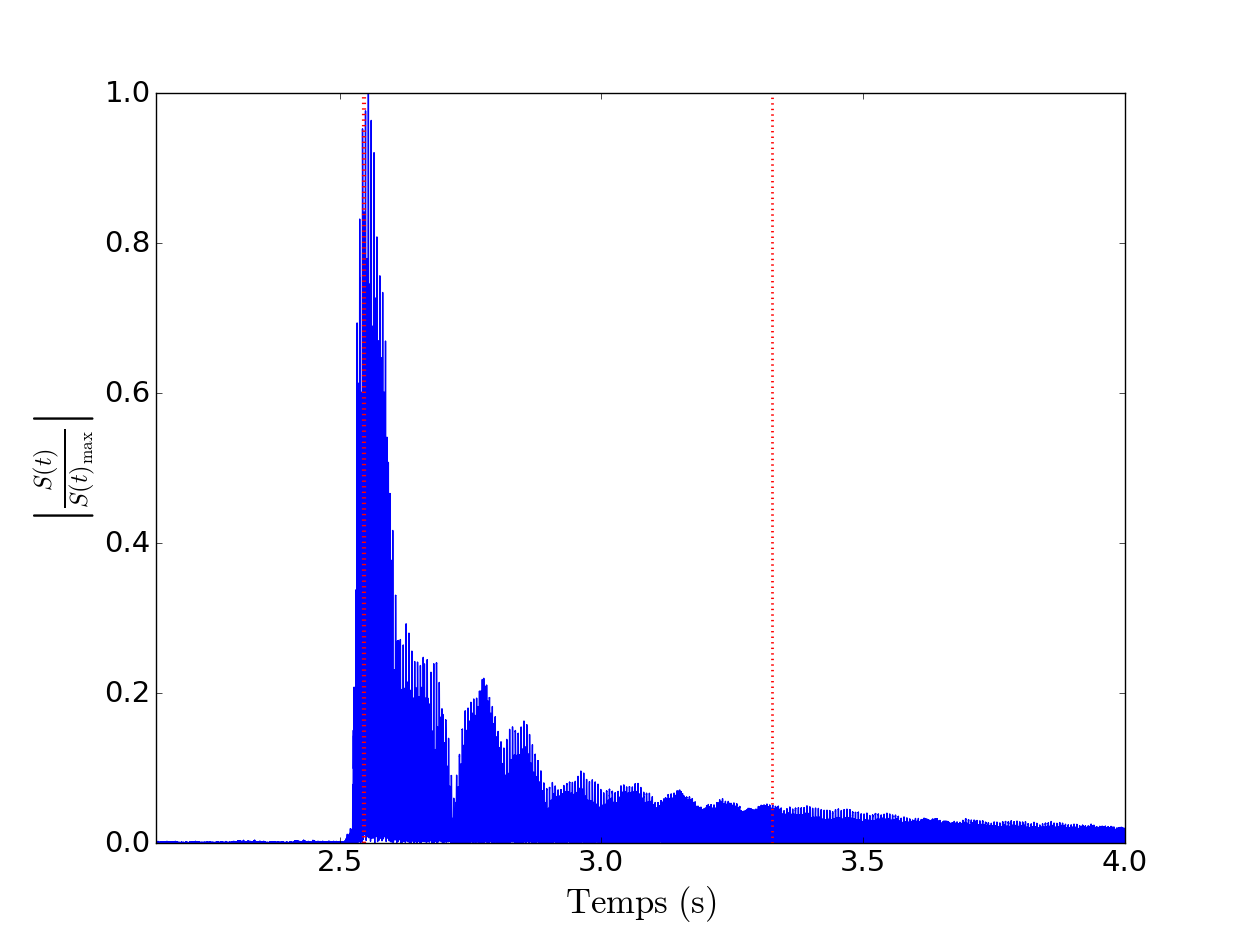
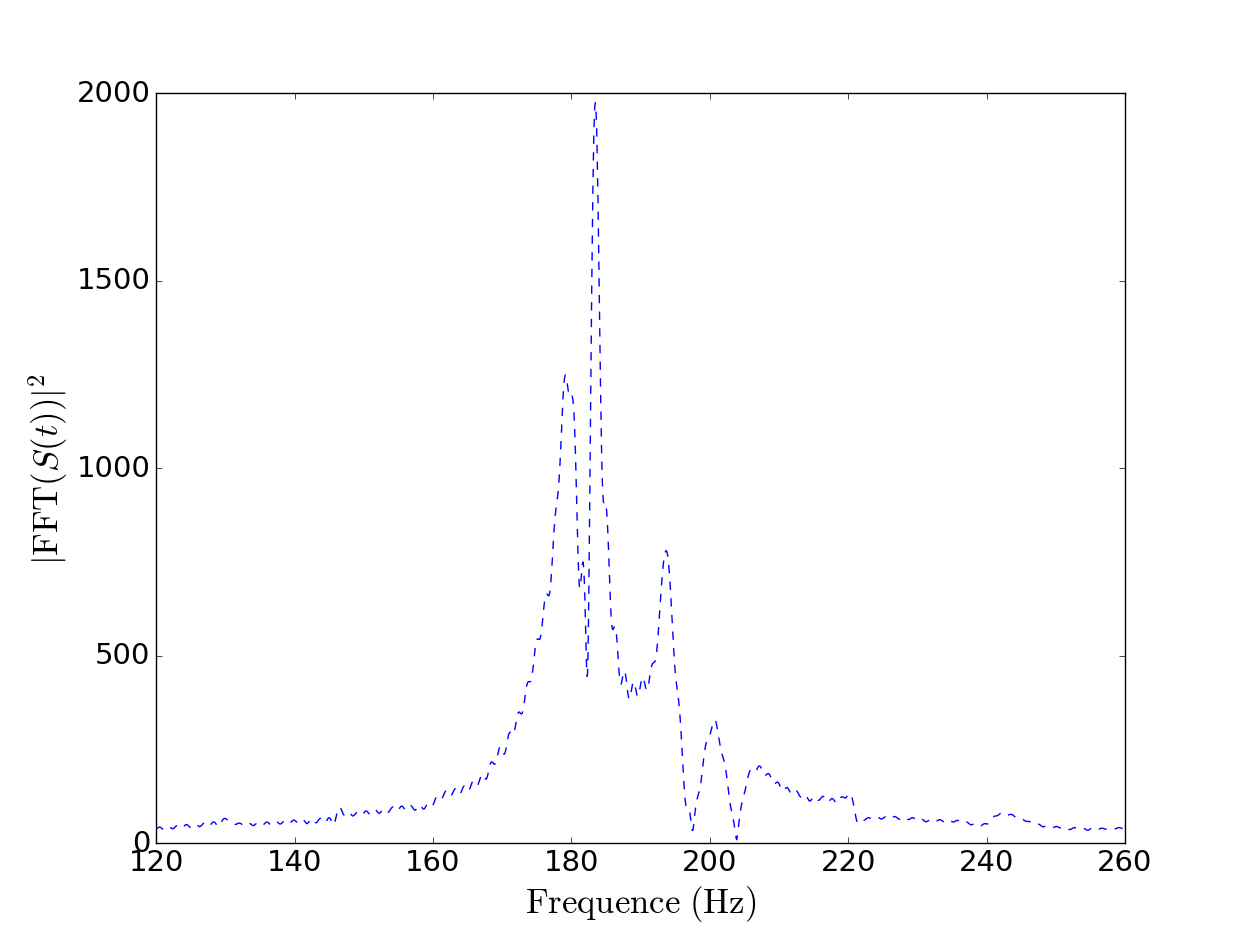
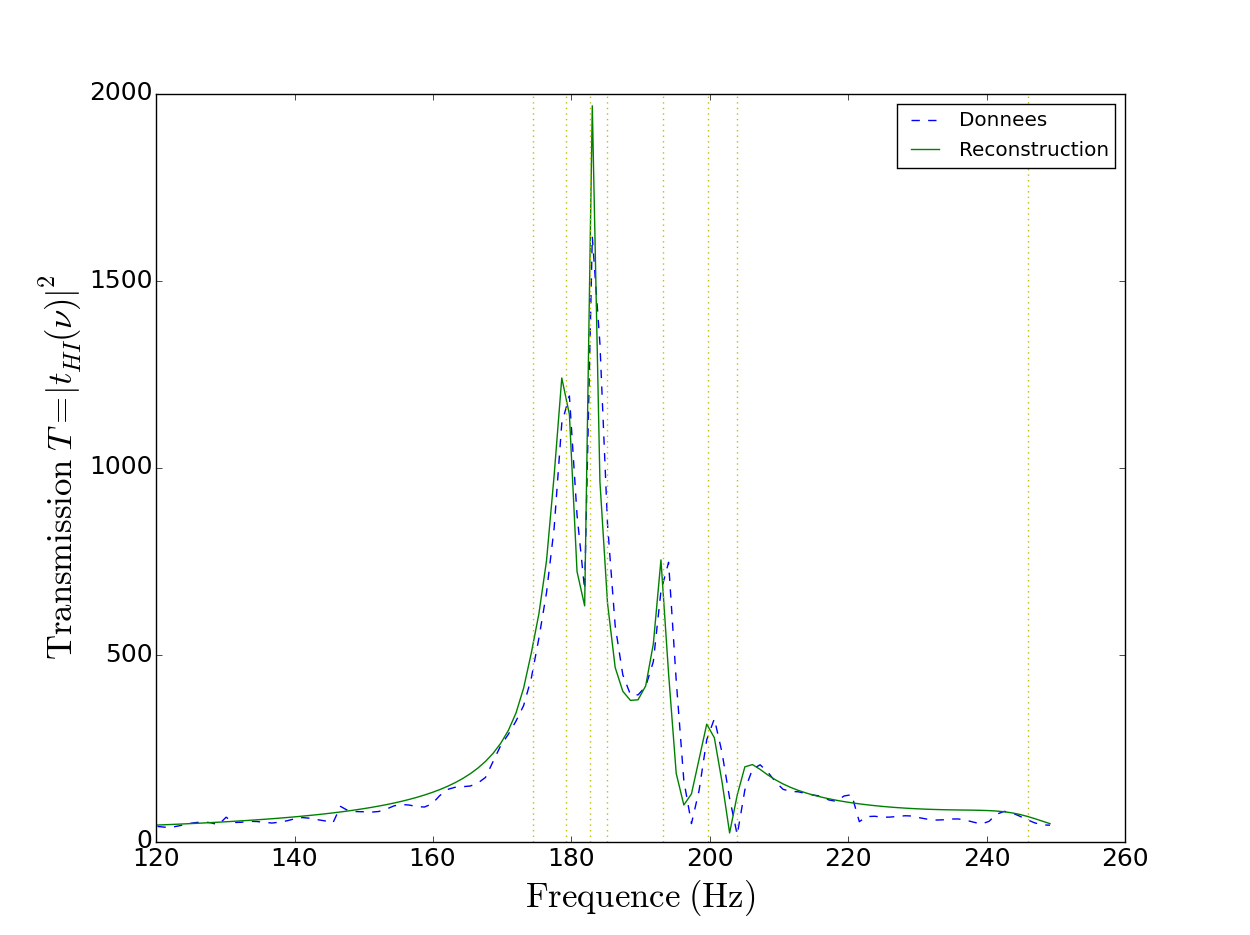
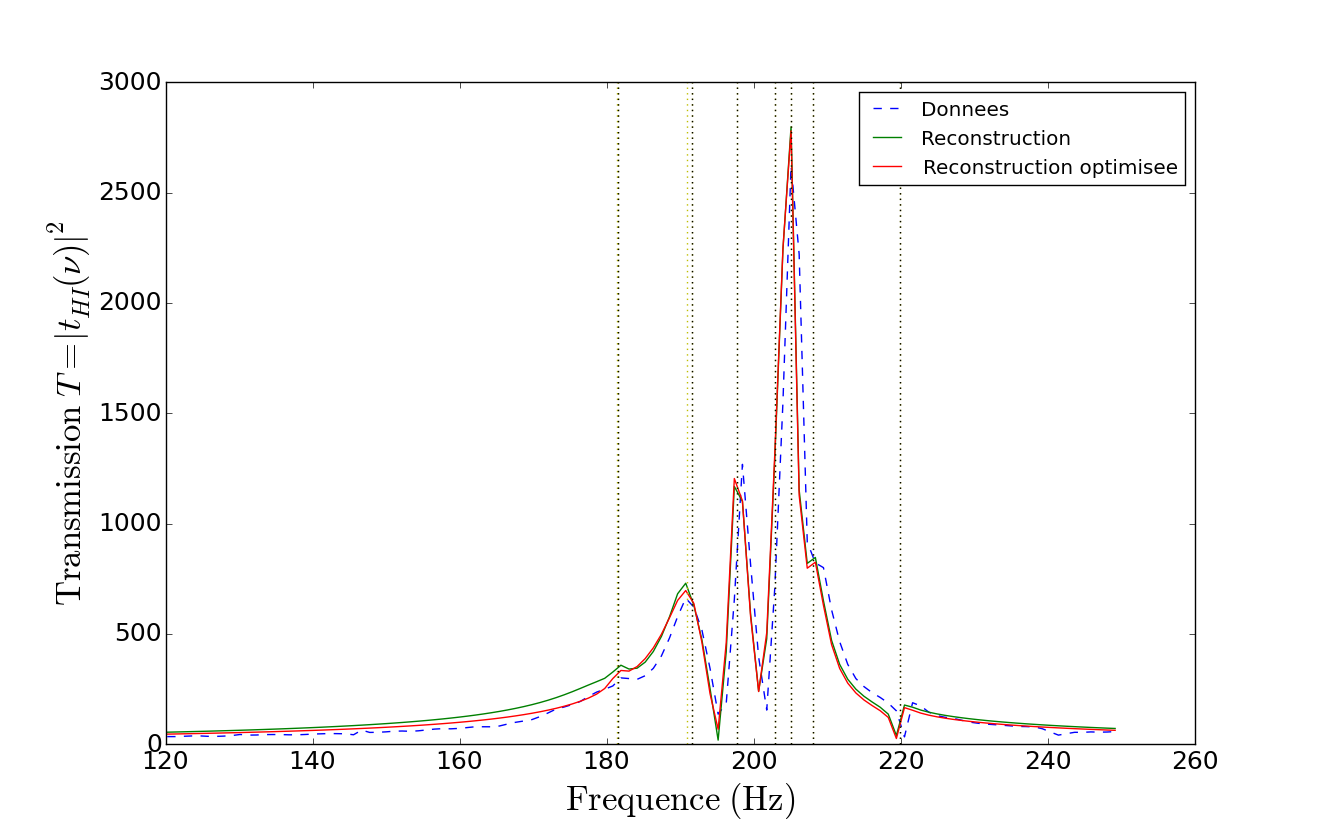
Figure 4 : À gauche, valeur absolue du signal normalisé en fonction du temps, les traits en pointillés rouges représentent de gauche à droite respectivement le temps $t_0$ et le temps $t_f$. À droite, module de la FFT du signal sur la fenêtre d’analyse temporelle allant de $t_0$ à $t_f$ en fonction de la fréquence sur un intervalle proche du loup.
Nous avons alors décidé de concentrer notre analyse sur deux séries d'enregistrements ayant été faits à des dates différentes. On observera par la suite que certaines conditions d'expérience ont changées entre ces deux enregistrements, notamment la façon dont la corde a été pincée, et montrerons quelles en sont les conséquences sur notre analyse.
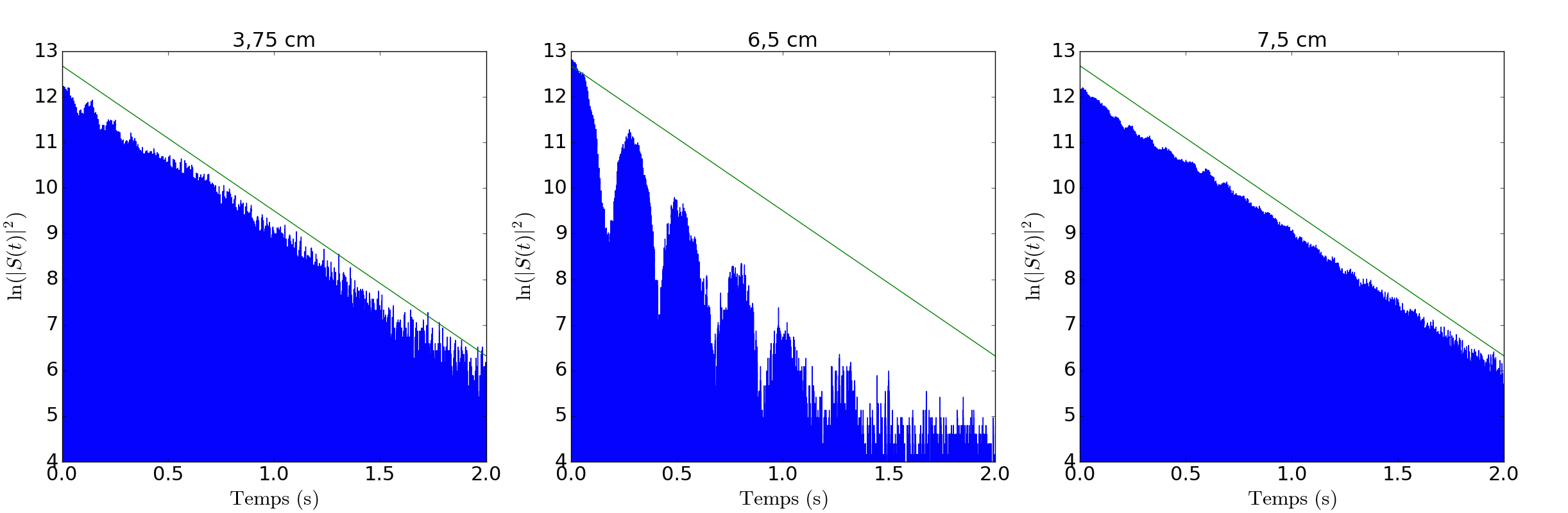
La première analyse nous permettant d'estimer la position du loup (la position du doigt sur la touche correspondant à la note du loup) s'est faite en observant le graphe du logarithme du signal carré de chaque fichier et a été détaillée dans le rapport). On avait déterminé que le fichier correspondant à la position 6,5.wav était celui où le loup serait le plus présent car c'est celui qui présente le plus de battements dans cette représentation des signaux :
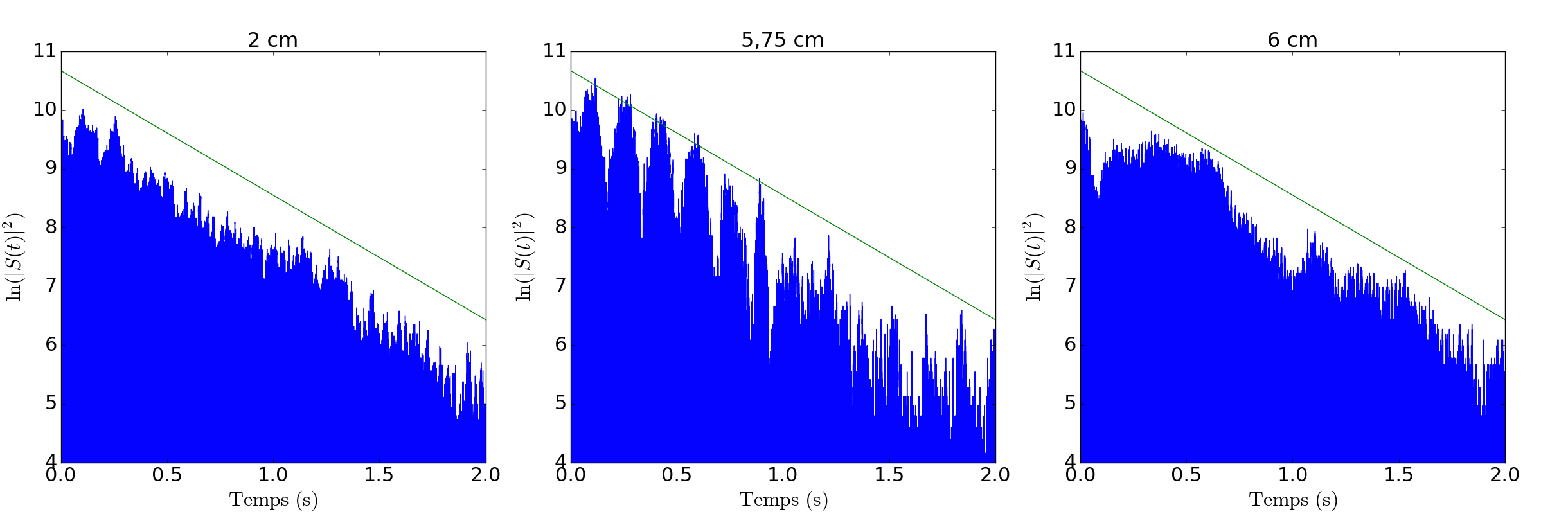
Nous avons appliqué la même méthode sur les fichiers "14 avril sans theunis" afin de déterminer à quelle position du doigt sur la touche chercher le loup. En effet, bien que les enregistrements du 14 et 21 avril ont été faits sur le même violoncelle, les conditions d'enregistrement changeantes (la température ambiante influence le couplage corde/corps et donc la position du loup, la position du micro a peut-être changé, et la corde n'a peut-être pas été pincée de la même manière) font que la position du doigt sur la touche correspondant au loup n'est pas forcément la même sur les fichiers du 14 avril et 21 avril.
Pour avoir une première vue d'ensemble de l'évolution de chaque résonance, nous avons tracé, sur un même graphe "en cascade" l'analyse en fréquence de chaque fichier pour les enregistrements du 21 et 14 avril.
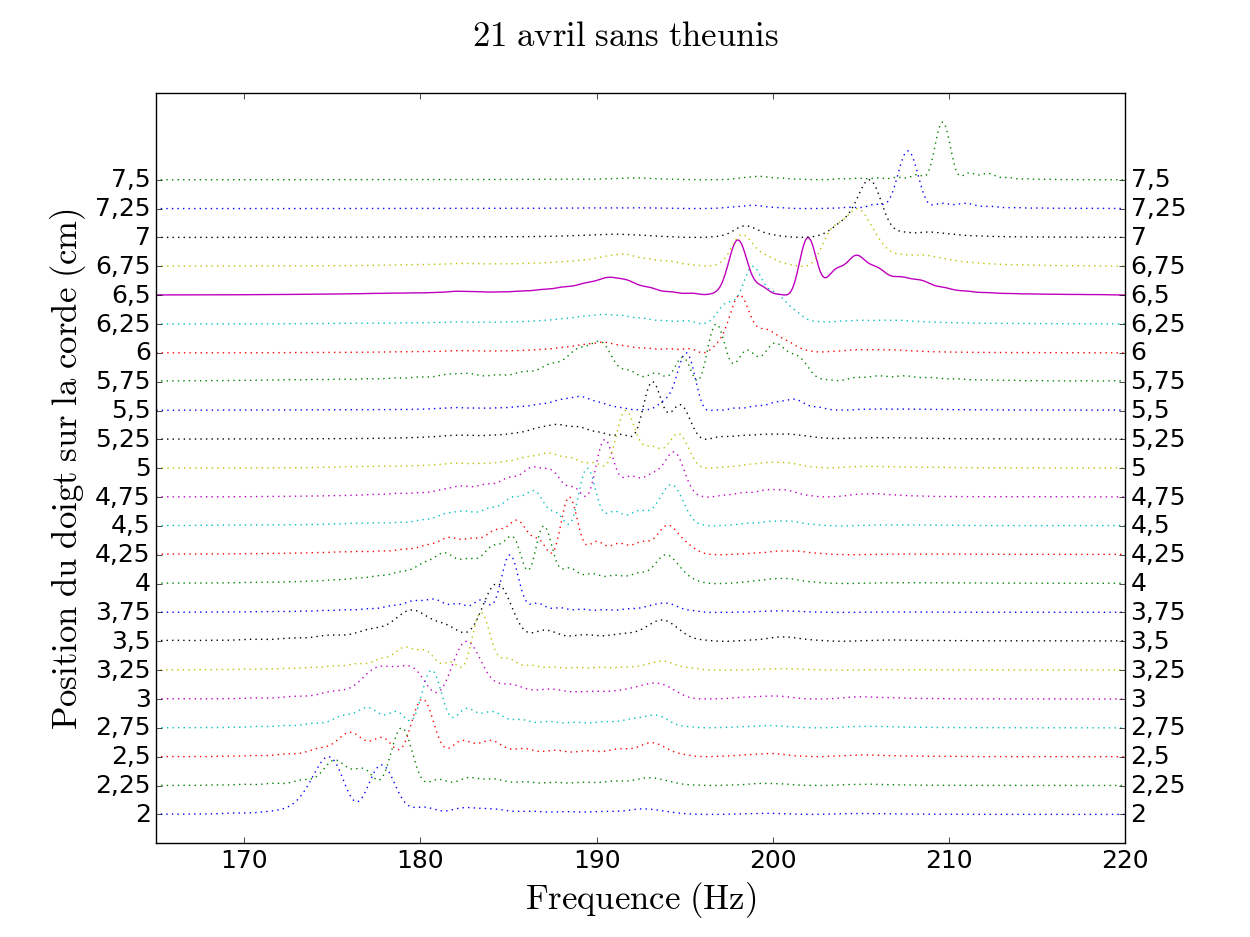
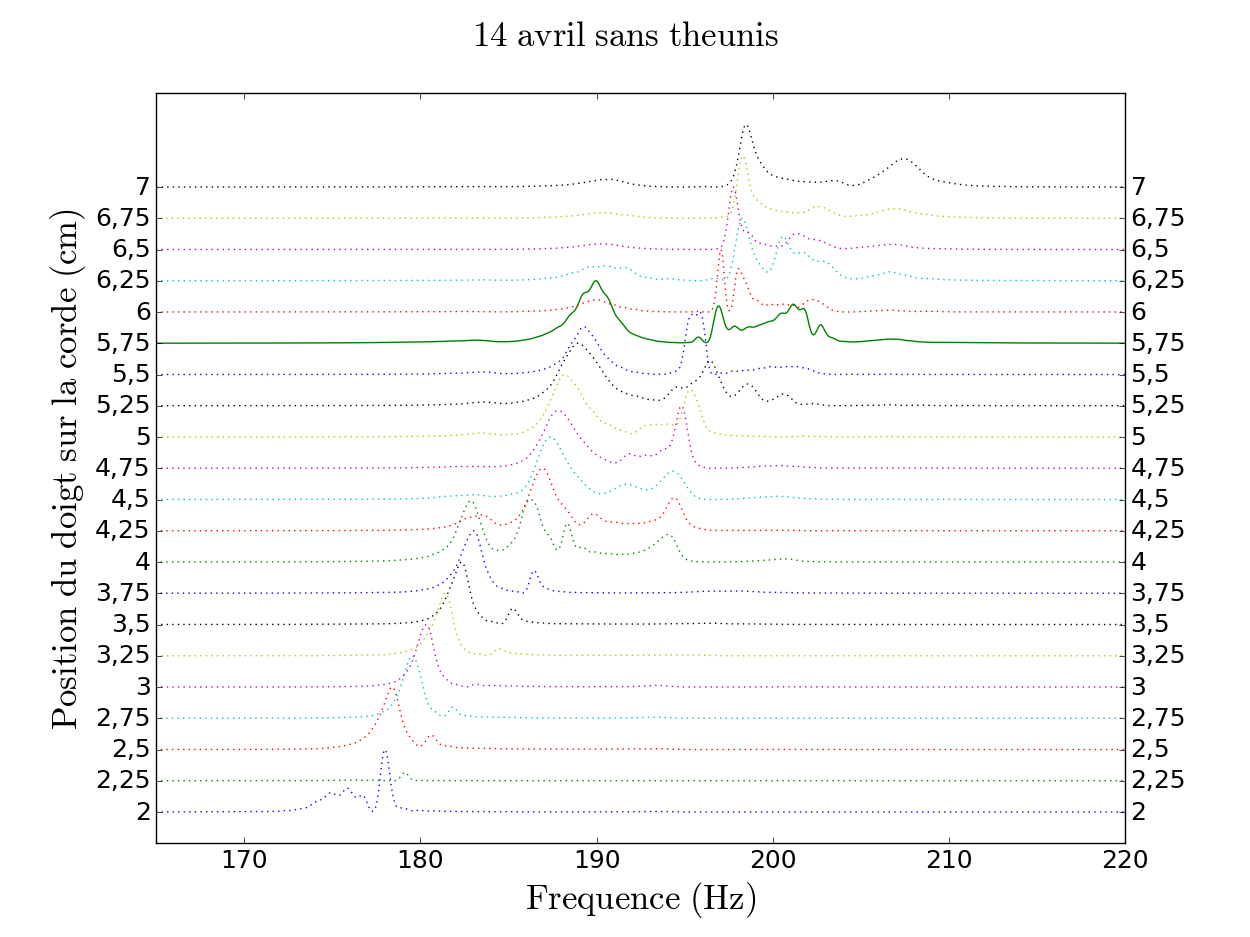
Dans cette représentation, nous voyons clairement l'évolution d'une résonance dont la fréquence croît avec la position du doigt sur la corde (en ordonnées croissantes). Plus le doigt se rapproche du chevalet, plus cette résonance est de fréquence haute : il s'agit donc de la résonance de la corde. Nous avons tracé en trait plein la courbe correspondant à la position du doigt que nous avons déterminée plus tôt comme correspondant à celle du loup pour chacune des deux séries d'enregistrement. Dans cette représentation, la présence d'un couplage fort ou couplage faible n'est pas très visible, ni le nombre de résonances présentent dans chaque fichier mais il permet de donner une première idée du phénomène. Nous avons alors poursuivi notre analyse en utilisant une méthode nous donnant plus d'information sur les résonances présentent dans chaque fichier.
Harmonic Inversion
L'Harmonic Inversion (HI) est une méthode numérique permettant d'extraire les résonances d'un signal et de reconstruire ce signal avec une somme
de lorentziennes. Cette méthode permet en effet d'extraire les résonances de signaux très complexes où il devient extrêmement difficile de
différencier les résonances entre elles. Ce procédé numérique suppose que le signal en question est une somme de sinusoïdes à décroissance
exponentielle. On fait alors l'hypothèse que l'on peut décrire le signal sonore que l'on étudie comme la partie réelle d'une somme d'exponentielles complexes amorties telle que : $S(t) = \sum \limits_{n=0}^N a_n \cdot \text{e}^{2 i \pi \nu_n t} \cdot\text{e}^{{-\frac{\Gamma_n}{2} t}}$. Ainsi, chaque résonance
peut être assimilée à une lorentzienne de la forme $ \frac{a_n}{\nu^2 - \left( \nu_n + \frac{\text{i}}{4\pi}\Gamma_n\right)^2}$.
Le programme réalise dans un premier temps la Transformée de Fourier Rapide (FFT) du signal, on obtient alors : $\tilde S(\nu) = \text{FFT}(S(t))$.
Dans un second temps, nous choisissons un intervalle de fréquence $\Delta \nu = \nu_1-\nu_0$ (avec $\nu_0$ ⩽ $\nu_1$) intéressant pour l'étude,
c'est-à-dire qu'on se place aux alentours de la fréquence du loup (typiquement $\Delta \nu$ de 120 Hz à 250 Hz). En utilisant la
fonction de Heaviside (ou fonction marche) $\mathcal{H}(\nu)$, on peut décrire l'opération c'est-à-dire qu'on obtient la fonction
$\Theta(\nu, \nu_0, \nu_1) = \mathcal{H}(\nu-\nu_0)-\mathcal{H}(\nu-\nu_1)$ ce qui donne la fonction sur laquelle l'Harmonic Inversion réalise l'extraction des résonances : $t_{HI}(\nu) = \tilde S(\nu)\cdot\Theta(\nu, \nu_0, \nu_1)$. On peut alors considérer la transmission du signal $T$ en fonction de la fréquence $\nu$, soit : $T=|t_{HI}(\nu)|^2$.
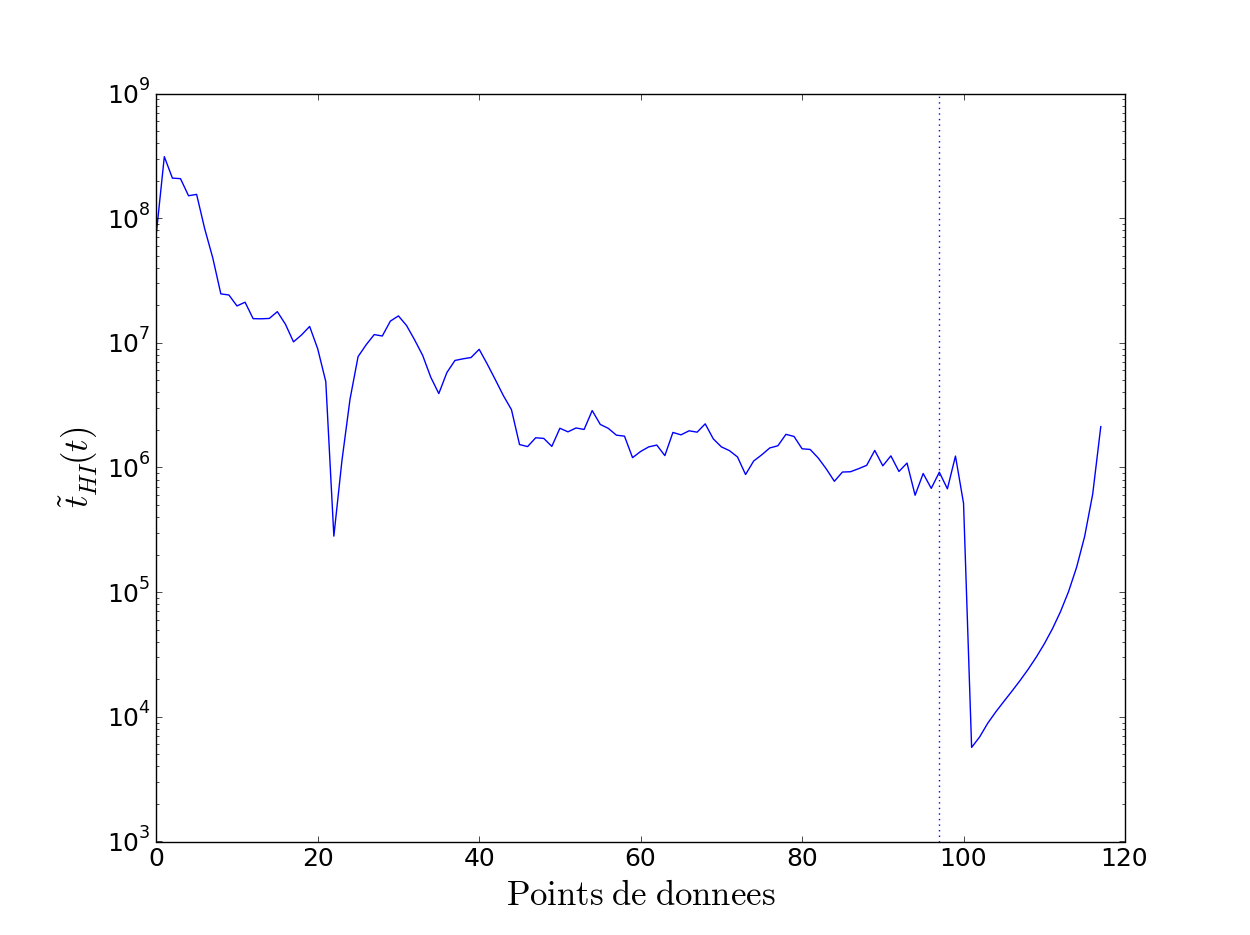
Le programme réalise, de plus, la Transformée de Fourier inverse sur l'intervalle $\Delta \nu$ afin de nous permettre de choisir un petit nombre de points ($2N$) en faisant attention de ne pas prendre en compte le bruit du signal, soit : $\tilde t_{HI}(t)=\text{FFT}[\tilde t(\nu)\cdot\Theta(\nu,\nu_0,\nu_1)]$. Par la suite, le programme va extraire de notre intervalle $N$ résonances en effectuant de nombreux tests pour ne considérer que les résonances a priori vraiment existantes. On peut ensuite reconstruire le signal avec une somme de lorentziennes, soit : $t_{HI}(\nu) = \sum \limits_{n=1}^N \frac{a_n}{\nu - \tilde{\nu}_n}+c_1\nu + c_0$ avec $\tilde{\nu}_n = \nu_n + \frac{i}{4 \pi}\Gamma_n$.
Application aux enregistrements
Afin d'étudier les résonances mises en jeu lors du phénomène du loup, nous allons appliquer l'Harmonic Inversion aux séries d'enregistrements réalisés par le groupe précédent le 21 avril 2016 et le 14 avril 2016. L’Harmonic Inversion prend en compte quatre paramètres pour réaliser l’extraction des résonances et la reconstruction du signal en somme de lorentziennes : $\delta t$ et $\Delta t$ (définis précédemment) ainsi que le nombre de points considérés pour l’analyse $2N$ (qui correspond à $N$ résonances) et le seuil d’amplitude $A_{seuil}$ à partir duquel le programme garde la résonance ou non. Dans un premier temps, nous avons représenté sur le même graphe, pour chaque fichier, la transmission du signal (en pointillés bleus) dans un intervalle proche du loup (typiquement de 120 à 250 Hz) ainsi que la reconstruction en somme de lorentziennes grâce à l’HI (en traits pleins verts), les résonances permettant cette reconstruction étant indiquées par des traits en pointillés jaunes. On trace également la FFT inverse de la FFT du signal pour avoir accès au nombre de points $2N$ (représenté par un trait vertical en pointillés bleus) que l’on va considérer pour l’HI, on fait alors en sorte de prendre un nombre de points cohérent vis-à-vis du graphe. Pour chaque fichier, on s’est attaché à trouver des valeurs $A_{seuil}$ et $2N$ telles que la reconstruction du signal en somme de lorentziennes soit la plus fidèle possible aux données (pour quelques fichiers, on a eu à changer un petit peu les valeurs de $\delta t$ et $\Delta t$).
Le programme Harmonic Inversion, dont le code a été développé sous Python par Ulrich Kuhl, est une fonction qui prend en entrée la transformée de fourier du signal et les paramètres $\delta t$, $\Delta t$, $2N$ et $A_{seuil}$ et donnera en sortie une liste contenant pour chaque fichier la liste des résonances, chacune caractérisée par sa fréquence, sa largeur, son amplitude et sa phase.
Pour étudier les nombreuses résonances qui entrent en jeu lors de la note du loup, nous avons voulu observer l'évolution de chaque résonance en fonction de la fréquence de la note jouée. Pour ce faire, nous avons représenté sur le même graphe la position de chaque résonance pour chaque fichier : en ordonnée, on a la position du doigt sur la touche et en abscisse, on a la fréquence en Hz. On repère par un point la position de chaque résonance qui a été trouvée par l’HI pour tous les fichiers enregistrés le 21 avril 2016 par exemple. La hauteur de chaque résonance est calculée en divisant son amplitude absolue par sa largeur. On l'a représentée pour chaque résonance en niveaux de gris, le blanc correspondant à la plus petite hauteur et le noir à la hauteur maximale. Le but de cette représentation sera d’essayer de relier les points correspondant à une même résonance pour tous les fichiers sonores afin d’étudier l’évolution des résonances en fonction de la fréquence de la note jouée.
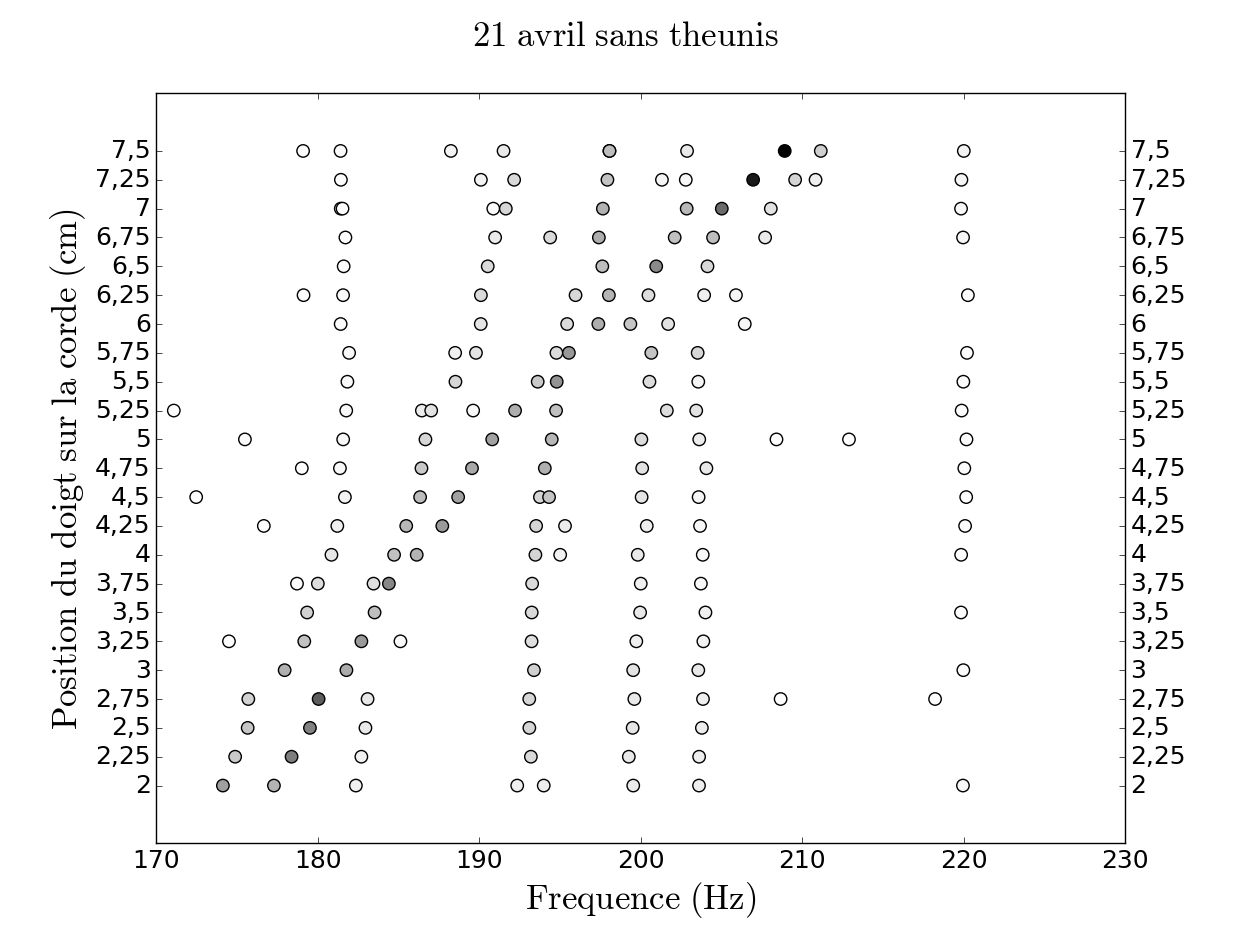
On remarque sur ce graphe la présence d’un nombre très important de résonances et certaines semblent erronées (résonances présentes seulement sur un ou deux fichiers, très éloignées des autres par exemple). Dans un premier temps, nous avons essayé de nettoyer le graphe précédent, c'est-à-dire que nous avons regardé chaque fichier séparément afin de vérifier que les résonances trouvées par l’HI sont pertinentes. Nous avons réalisé un programme en Python qui permet de modifier en temps réel les résonances, c'est-à-dire qu’on peut supprimer des résonances ou bien, dans le cas où deux résonances sont vraiment très proches, quasiment confondues, on a la possibilité de créer une résonance de fréquence égale à la moyenne des deux fréquences et d’amplitude absolue égale à la somme des deux amplitudes. Le programme permet de visualiser la reconstruction en somme de lorentziennes qui prend en compte les modifications effectuées sur les résonances afin de bien vérifier que la reconstruction est toujours pertinente.
Le programme que nous avons codé en python nous donne une représentation (figure 9) interactive nous permettant de connaitre, simplement par clic-droit sur un point, la fréquence, largeur, hauteur et amplitude de la résonance représentée par le point. De plus, nous avons programmé la possibilité d'éliminer une résonance par clic-gauche et de la fusion de deux résonances par clic-molette lorsque nous jugions que l'Harmonic inversion avait mal interprété une résonance unique (nous avons comparé pour chaque cas l'amplitude et la hauteur des deux résonances pouvant être fusionnées). Après avoir effectué la vérification de chaque résonance pour tous les fichiers sonores, on a obtenu le graphe "nettoyé", présenté ci-dessous, qui représente les résonances en fonction des fichiers.
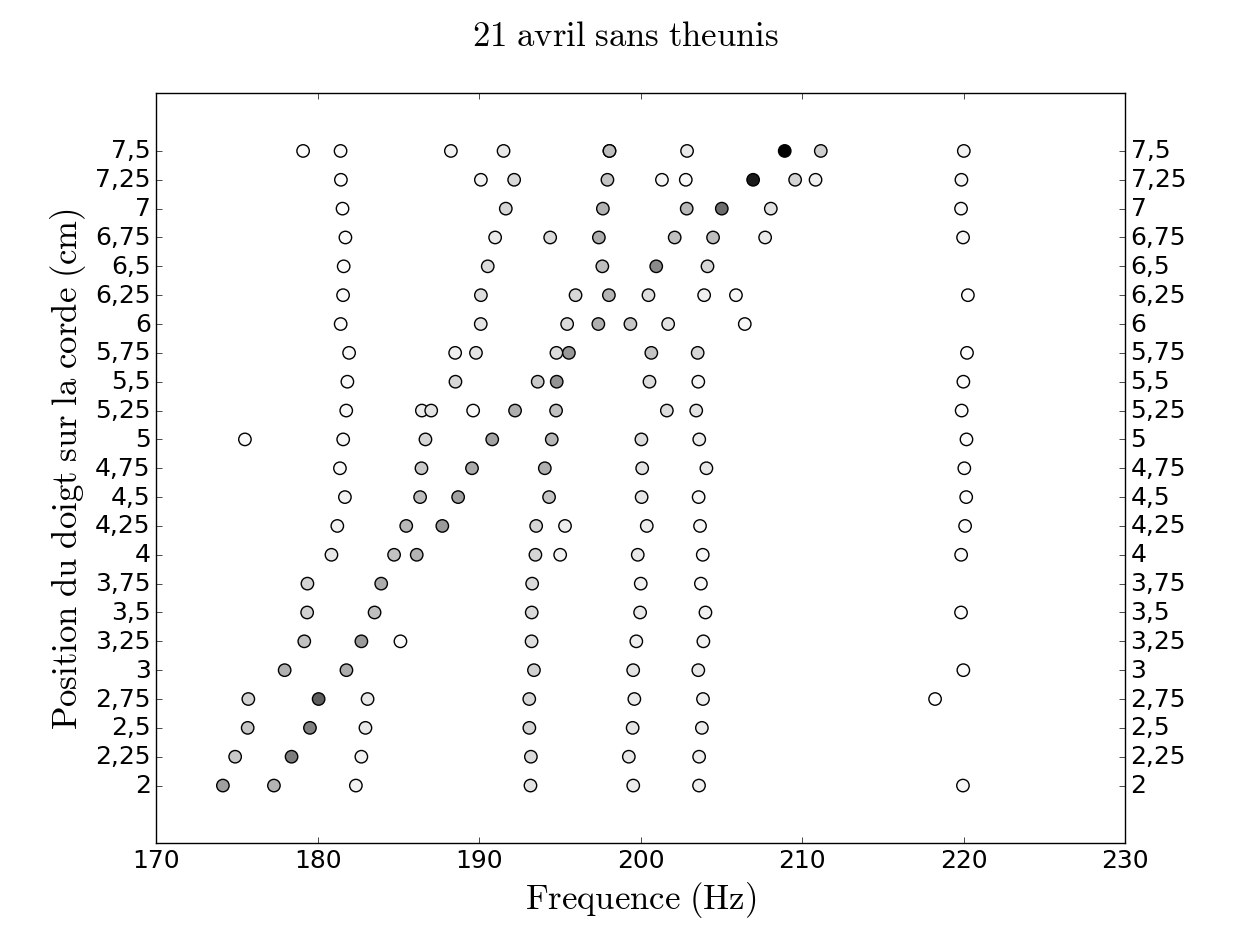
À l’aide de ce graphe, nous avons essayé de relier les points correspondant à chacune de ces résonances. On s’est intéressé tout particulièrement aux deux résonances principales mises en jeu lors du phénomène de la note du loup. Il s’agit, d’une part, de la résonance de la corde qui correspond à la hauteur de la note jouée et, d’autre part, de la résonance du corps qui reste à une fréquence fixe. Pour relier les bonnes résonances, on a étudié la largeur de chaque résonance en fonction du fichier et on a fait en sorte que les largeurs de ces deux résonances se croisent à hauteur du loup. On s’est également servi de la hauteur des résonances qui est indiquée par le niveau de gris du point représentant la résonance.
Pour une meilleure compréhension, nous avons également mis en évidence deux zones sur le graphe : le rectangle jaune qui délimite la zone où l'on devrait s'attendre à un rapprochement des fréquences et un croisement des largeurs d'après l'analyse faite auparavant (figure 5) et le rectangle bleu, plus large en ordonnée du fait de l'incertitude de l'Harmonic Inversion, qui représente la zone où on observe le croisement après avoir relié les points à la main. L'idéal étant de trouver une configuration où ces deux zones sont le plus confondues, nous avons tenté plusieurs identifications possibles des résonances.
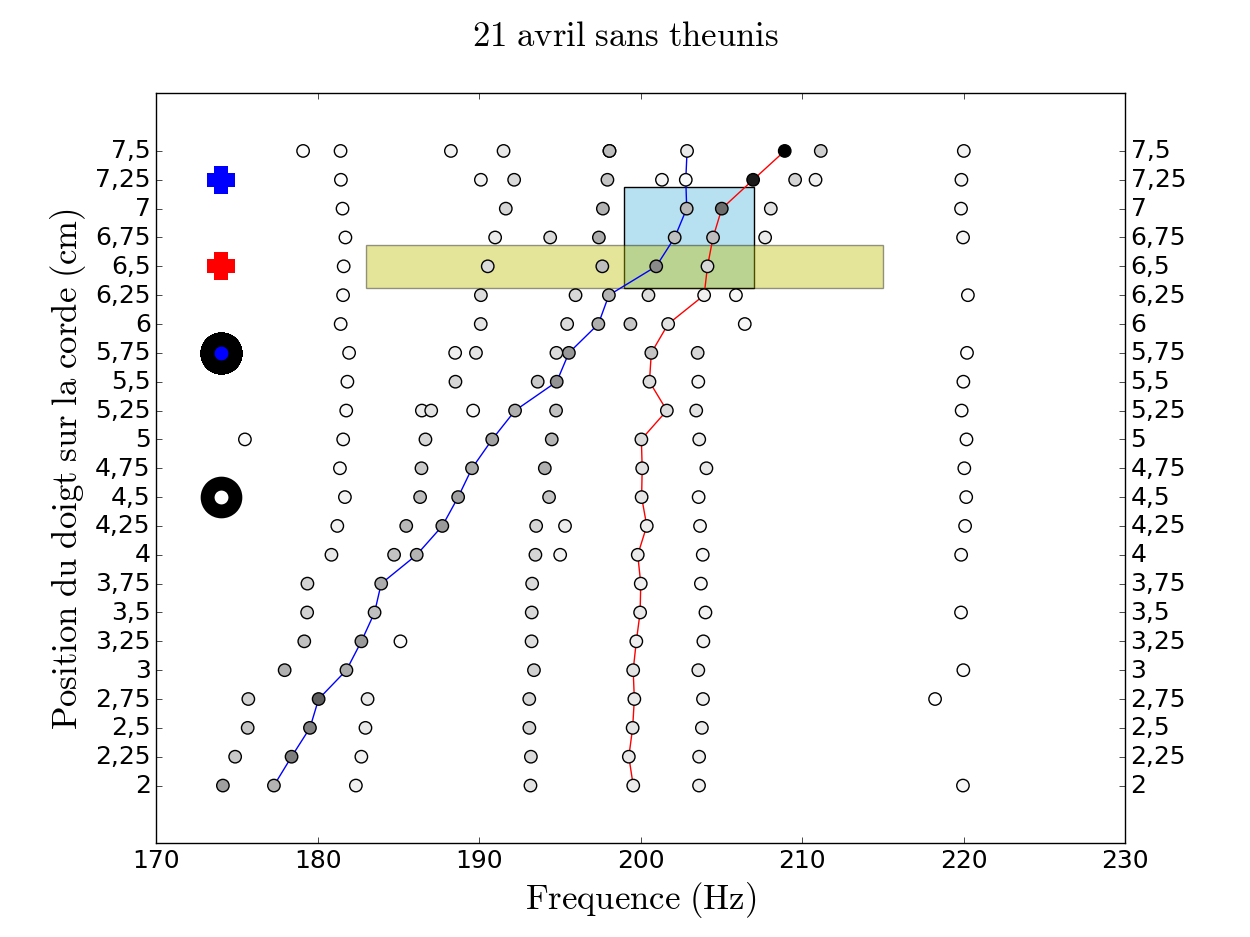
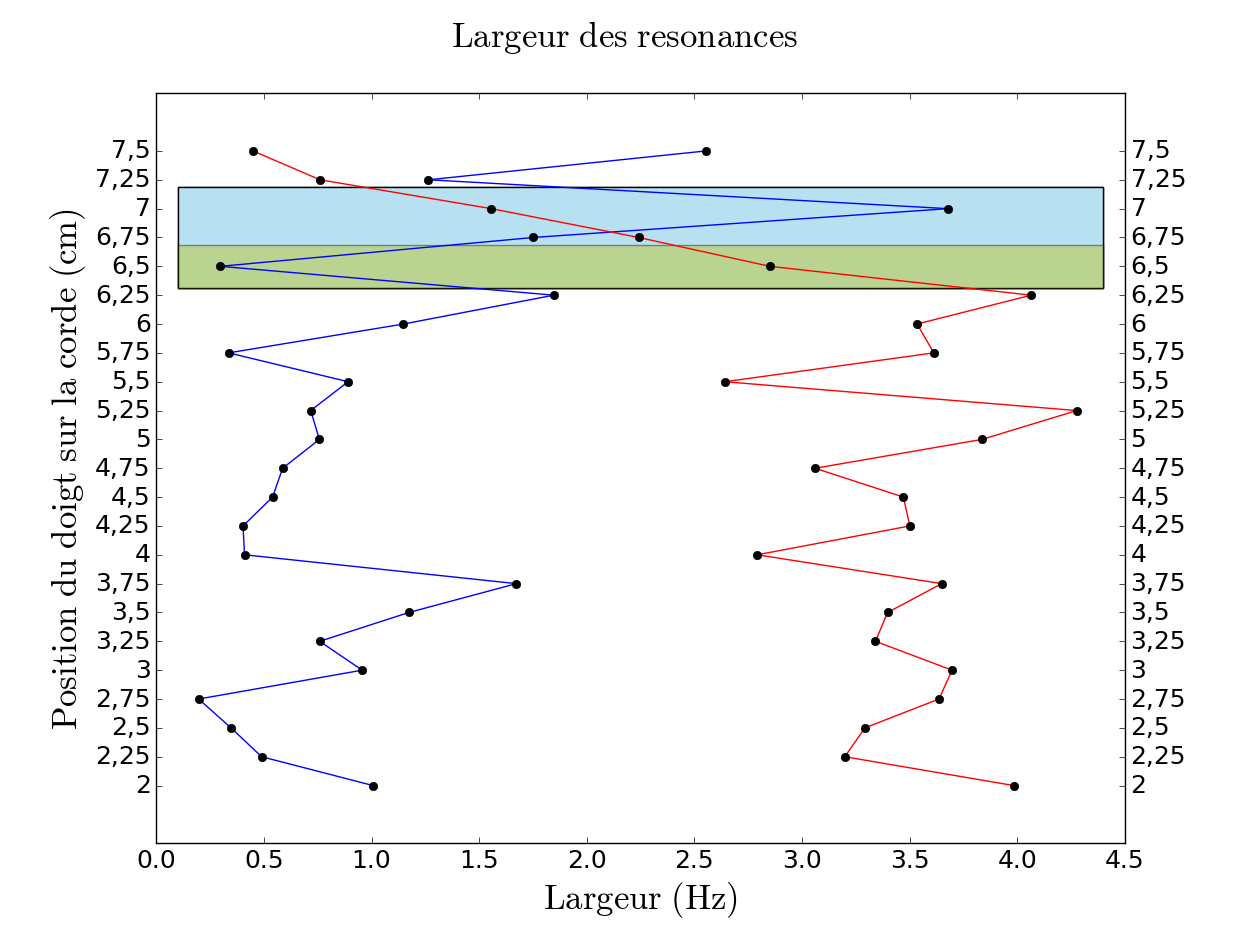
Sur la figure 12, qui représente la meilleure configuration que l'on ait pu avoir, nous voyons un évitement des deux courbes dans la zone bleue. À droite les largeurs correspondantes, on voit clairement le croisement de ces dernières entre les ordonnées 6,75 cm et 7 cm ce qui correspond en effet à l'ordonnée où les points en fréquence sont les plus rapprochés (figure de gauche). Pour cette figure 12, c'est à la position de 7 cm que les deux points sont les plus proches en fréquence avec une distance de 2,173 Hz (le point de gauche ayant une fréquence d'environ 205,027 Hz et celui de droite 202,854 Hz).
Le loup se situerait donc aux alentours de 200/205 Hz avec un désaccord d'environ 2 Hz, ce qui est un peu plus élevé que les prévisions théoriques faites dans la partie précédente mais est en total accord avec notre analyse numérique depuis le début. Nous avons donc essayé d'autres combinaisons afin de vérifier s'il n'y avait pas de meilleur résultat concernant les attentes théoriques.
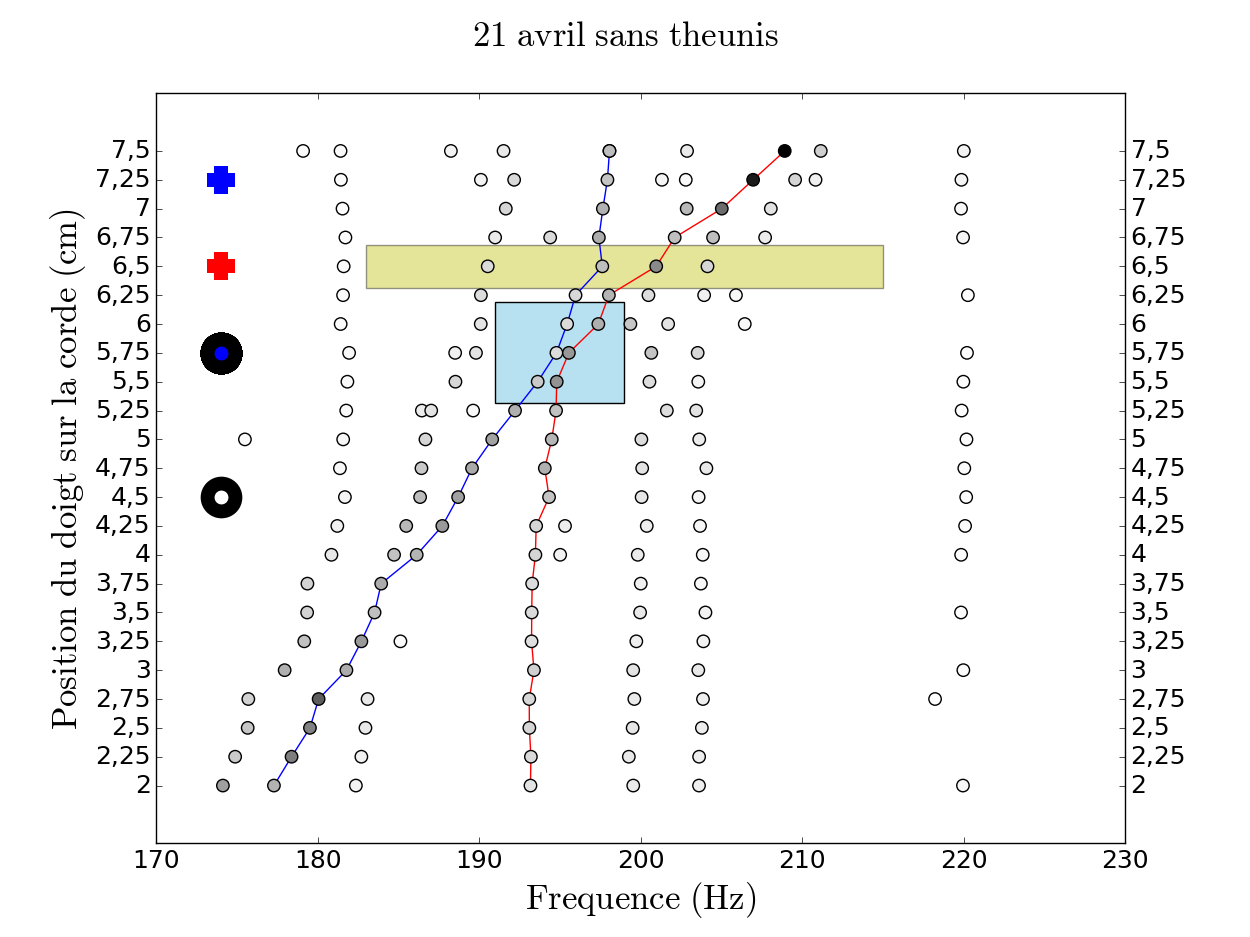
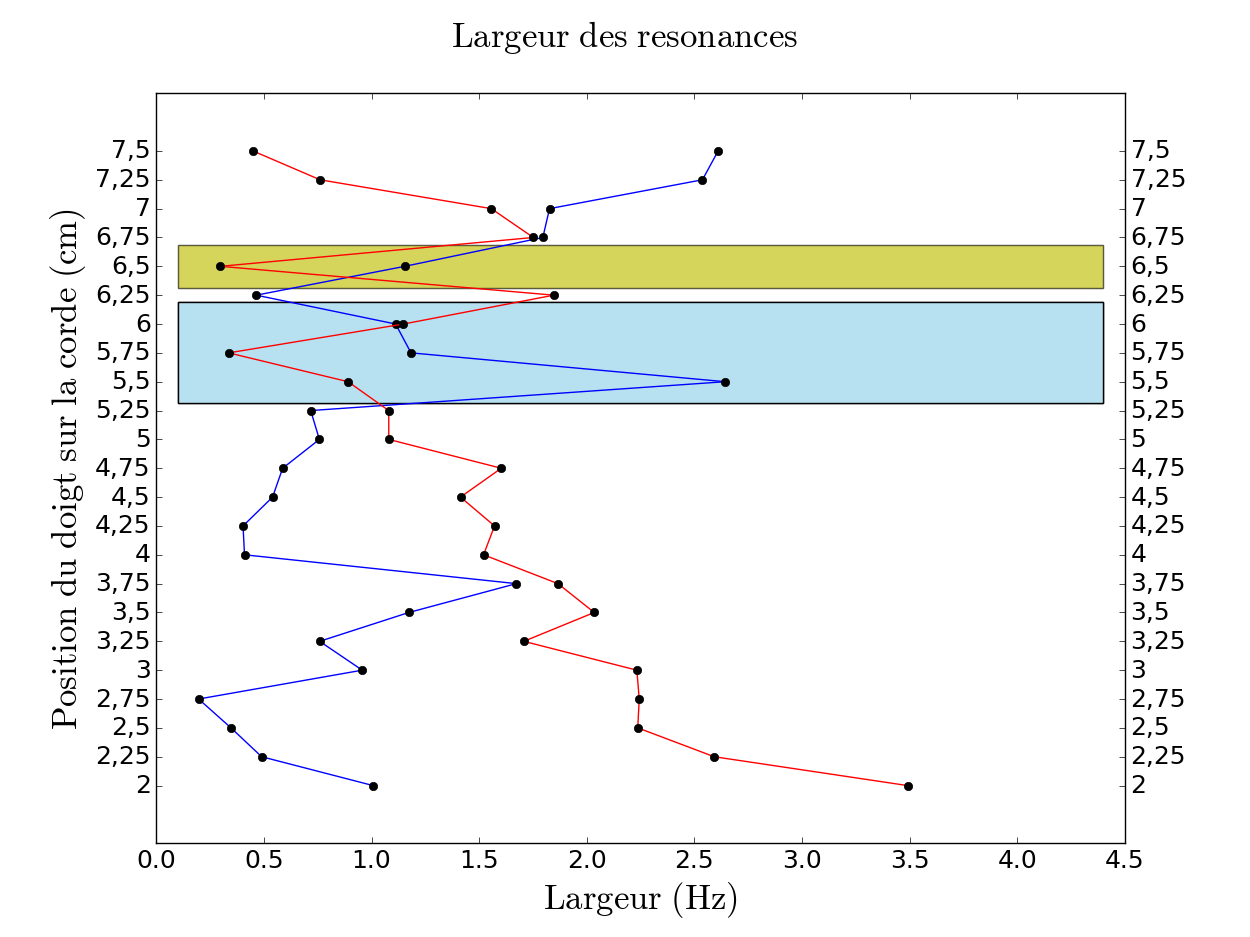
Sur la figure 13, on a représenté une autre combinaison possible, moins concluante que la première puisque le rapprochement en fréquence se fait à une fréquence plus éloignée des prévisions. De plus, on observe un croisement multiple des largeurs ce qui fait que nous préfèrerons le résultat représenté sur la figure 12. En revanche, cette combinaison a l'avantage de ne laisser pratiquement pas de points "libres" entre les deux courbes, ce à quoi l'on devrait s'attendre si l'on considère un modèle à deux résonances.
Nous pouvons donc déjà en déduire que le phénomène est plus complexe que le modèle théorique et prend en compte plus de deux résonances. La figure 12, qui est notre résultat le plus concluant, laisse entendre qu'il y aurait donc trois résonances entrant en jeu (on observe la suite de points démarrant aux alentours de 192 Hz).
On a par la suite fait la même étude sur les fichiers du 14 avril, représenté dans la figure ci-dessous :
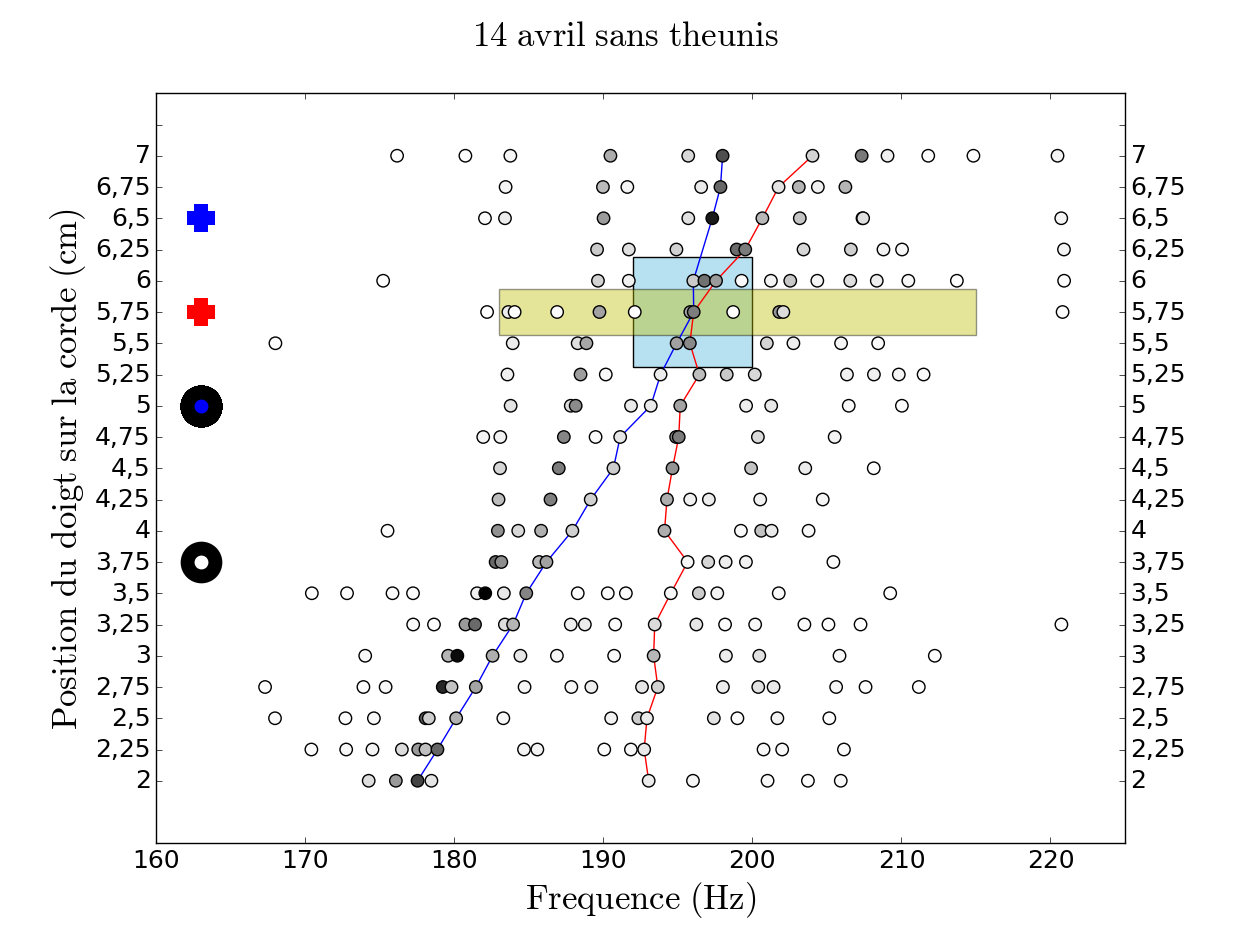
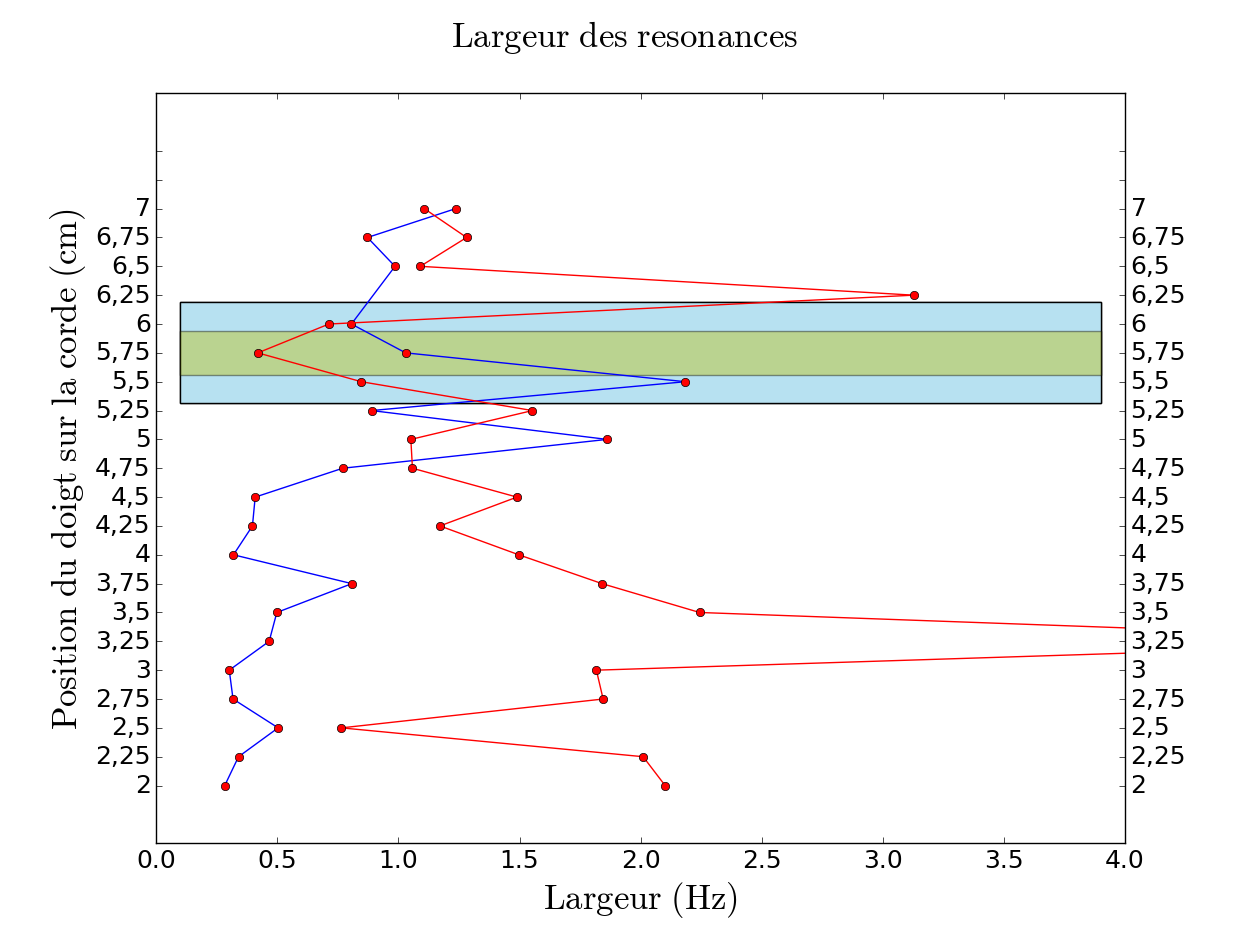
On observe sur la figure 14 tout d'abord plus de points que sur les figures précédentes, ce qui est dû au fait que les enregistrements du 14 et 21 avril ont été faits dans des conditions différentes et que les cordes n'ont pas été pincées exactement de la même manière. Le fait qu'il y ait plus de points vient à la fois du fait que la corde a été pincée d'une manière favorisant plus d'harmoniques mais aussi parce que nous avons décidé de changer les paramètres de l'Harmonic Inversion afin d'avoir plus de précision. En effet, nous avons décidé de prendre des temps plus longs (paramètre $\Delta t$) afin de pouvoir trouver potentiellement plus de résonances. La contrepartie est la présence de points dûs au bruit, que nous avons en partie éliminés.
Le croisement se situe dans la zone prévue (figure 6) mais la distance entre les points les plus proches (le désaccord) est faible (196,061 - 195,835 = 0,226 Hz). De même que pour la figure 13, les largeurs semblent se croiser plusieurs fois à proximité des zones jaunes et bleues.

