Modélisation mécanique simplifiée du phénomène

Le phénomène du loup consiste en une résonance couplée de la corde et de la table d'harmonie du violoncelle. Afin d'étudier ce phénomène faisant intervenir de nombreuses résonances de la corde et du corps, on utilise la modélisation d'un couplage corde-table d'harmonie donnée par Kergomard et Chaigne³. L'étude réalisée dans ce livre considère une corde de longueur $L$ fixée à une extrémité (i.e. fixée par le doigt sur la touche) et mobile à son autre extrémité (au niveau du chevalet), elle ne prend en compte que le déplacement transverse de la corde. En utilisant des considérations sur les énergies potentielles et cinétiques, Kergomard et Chaigne³ expriment trois matrices : la matrice de raideur $\mathbb{K}$ (supposée diagonale), la matrice de masse $\mathbb{M}$ et la matrice d'amortissement $\mathbb{C}$ (supposée diagonale). Afin de résoudre le problème analytiquement, on étudie pour la suite le couplage entre un seul mode de la corde et un seul mode de la table. On obtient dans ce cas les matrices suivantes : $$\mathbb{K= \begin{bmatrix} k_{11} & 0 \\ 0 & k_{22} \end{bmatrix} \quad= \begin{bmatrix} \frac{\pi^2}{2L}T & 0 \\ 0 & k_B+\frac{T}{L} \end{bmatrix} \quad}$$ où $L$ représente la longueur de la corde, $T$ sa tension et $k_B$ la constante de raideur effective du corps de l'instrument, $$\mathbb{M= \begin{bmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{bmatrix} \quad=\begin{bmatrix} \frac{\mu L}{2} & \frac{\mu L}{\pi} \\ \frac{\mu L}{\pi} & m_{B}+\frac{\mu L}{3} \end{bmatrix} \quad} $$ où $\mu$ représente la masse linéique de la corde et $m_B$ la masse effective du corps de l'instrument, $$\mathbb{C= \begin{bmatrix} c_{11} & 0 \\ 0 & c_{22} \end{bmatrix} \quad=\begin{bmatrix} 2\zeta_S\omega_Sm_{11} & 0 \\ 0 & 2\zeta_B\omega_Bm_{22} \end{bmatrix} \quad}$$ avec $\zeta_S$ et $\omega_{S}=\sqrt{\frac{k_{11}}{m_{11}}}$ représentant respectivement le coefficient d'amortissement et la pulsation propre découplée du mode fondamental de la corde; $\zeta_B$ et $\omega_{B}=\sqrt{\frac{k_{22}}{m_{22}}}$ représentant respectivement le coefficient d'amortissement et la pulsation propre du mode fondamental de la table. Ce système prend la forme classique, ainsi on obtient les équations différentielles suivantes : \begin{equation}\label{eq:diff} \mathbb{M}\ddot{q}+\mathbb{C}\dot{q}+\mathbb{K}q=0 \end{equation} Ce système d'équations différentielles conduit à l'équation caractéristique suivante que vérifient les pulsations propres du système couplé : \begin{equation}\label{eq:finale} (\omega_{S}^2 +2 j\omega \zeta_S\omega_S -\omega^2)(\omega_{B}^2 +2 j\omega \zeta_B\omega_B -\omega^2) = \omega^4 \lambda^2 \end{equation} où $ \lambda^2 = \frac{m_{12} m_{21}}{m_{11} m_{22}} = \frac{2\mu L}{\pi^2(m_{B}+\frac{\mu L}{3})} $ représente le coefficient de couplage massique.

Application à notre violoncelle

On a appliqué le modèle présenté précédemment au violoncelle utilisé lors du projet de l’année 2016, c’est-à-dire que l’on a calculé les pulsations propres du système couplé correspondant à l’équation précédente. Nous avons eu recours à certaines données qui ont été déterminées lors du projet précédent, notamment la raideur et la masse effective du corps de l’instrument (détails des méthodes sur le site internet Chasse au Loup²). Nous avons calculé toutes les autres données nécessaires à la résolution de l’équation en utilisant les caractéristiques du violoncelle comme la longueur de la corde de Do par exemple (détails des calculs sur notre rapport).
Nous avons ensuite utilisé le logiciel Mathématica afin de résoudre analytiquement l’équation de Kergomard et Chaigne³. On a alors obtenu deux couples de solutions complexes : ($\omega_1$, $-\omega_1^*$) et ($ \omega_2$, $\omega_2^*$) (avec $\omega_{1/2}^*$ complexe conjugué de $\omega_{1/2}$).Nous avons choisi les deux solutions qui possèdent des parties réelles positives. On a alors séparé la partie réelle et la partie imaginaire de ces solutions et on les a tracées en fonction du rapport $\Omega=\frac{\omega_B}{\omega_S}$.

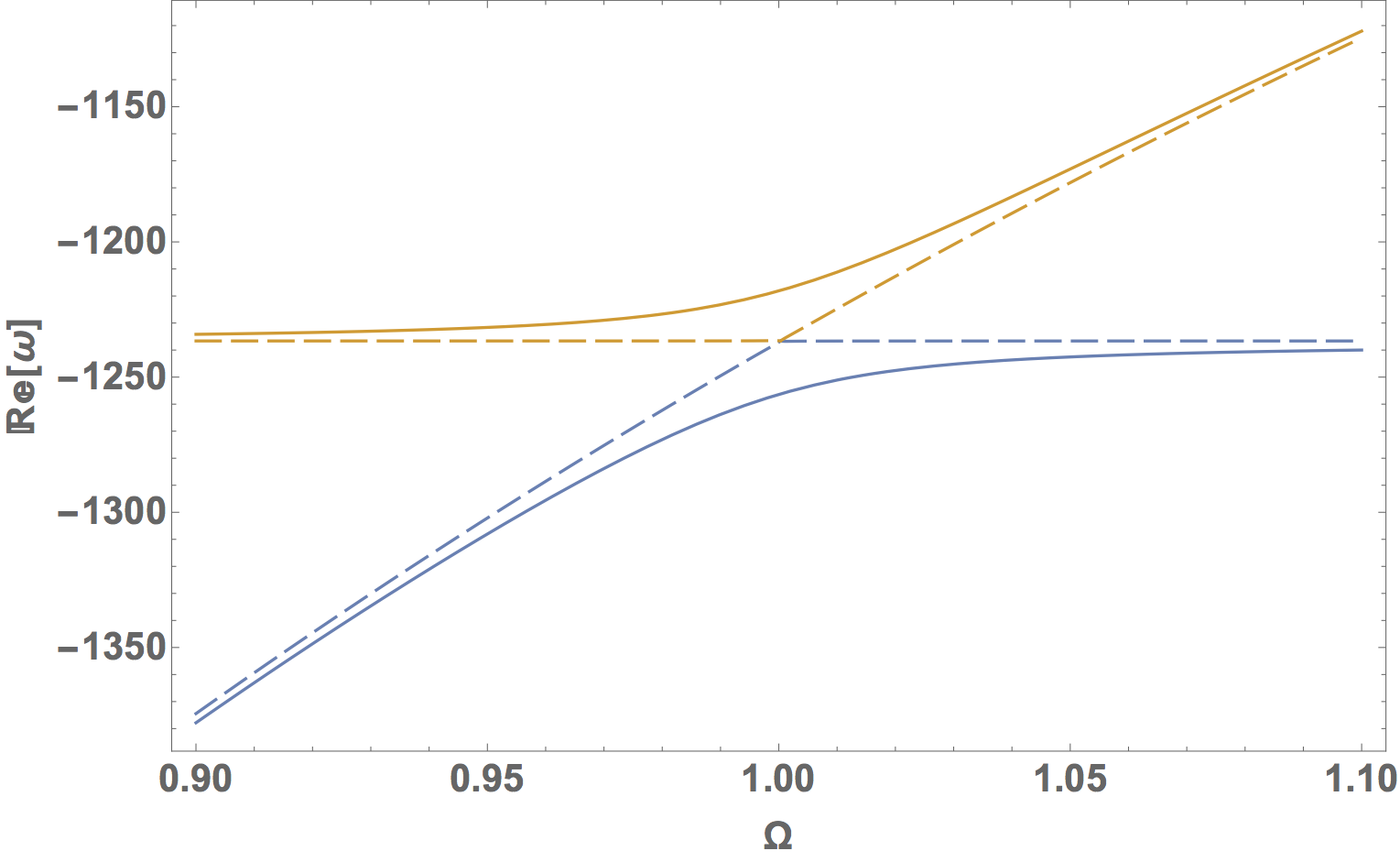
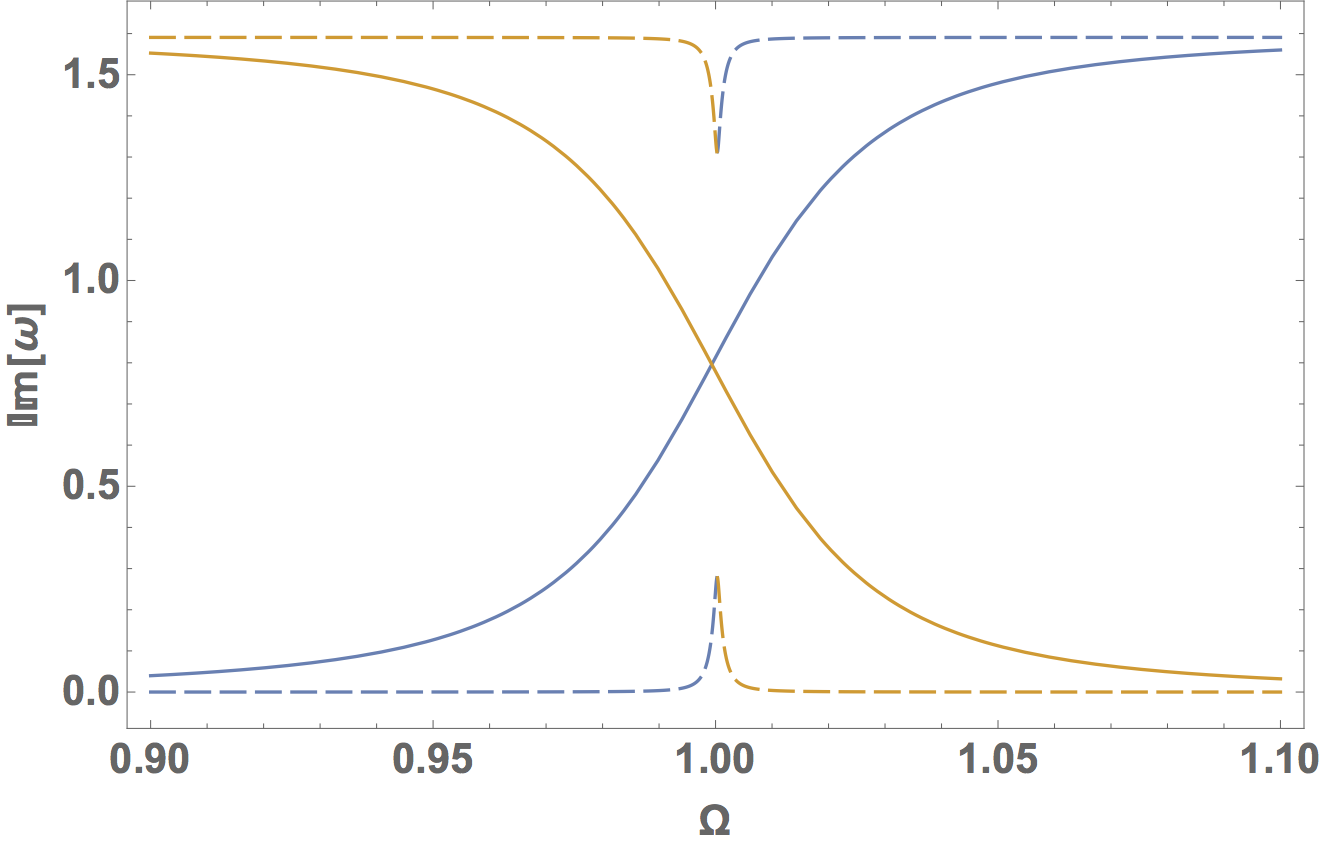
Figure 2 : Représentation d'un couple de solutions de l'équation caractéristique. À gauche, partie réelle et à droite partie imaginaire. En trait plein : valeurs obtenues avec notre violoncelle ($Q_B \simeq 417$). En pointillés : valeurs obtenues avec une dissipation augmentée artificiellement ($Q_B \simeq 13,2$).

Dans le cas des valeurs obtenues pour notre violoncelle, on observe un croisement évité des parties réelles au niveau de la note du loup (autour du point d’abscisse $\Omega = 1$). Cette zone de croisement évité de la partie réelle correspond à la plus petite différence possible entre les pulsations, c’est la différence de fréquences entre la fréquence de résonance d'un mode du corps et la fréquence de résonance d'un mode du corps dans le cas du couplage fort (décrit en introduction). L'espacement ici observé est caractéristique de la note du loup et c’est ce croisement que l’on va essayer de mettre en évidence en analysant les enregistrements sonores réalisés par le groupe de 2016. Pour cela, on aura recours à des outils mathématiques et notamment au procédé d’Harmonic Inversion que nous allons décrire dans la partie suivante.

Modèle quantique 2x2

En décrivant les résonances du loup sous forme de lorentziennes, il apparait que le phénomène du loup peut être assimilé à un système quantique à deux niveaux avec deux états |1⟩ et |2⟩. Il s’agit d’un cas de couplage entre ces états, ce qui implique un hamiltonien non hermitien si $\lambda$ et $\omega_0 \in \mathbb{C}$ mais toujours symétrique :

$$\mathbb{H= \begin{bmatrix} \omega_{0} & \lambda \\ \lambda & \omega_{0} \end{bmatrix} \quad}$$

où $\lambda$ est un coefficient de couplage et $\omega_0$ représente la pulsation propre du système. De plus, le système est amorti, on introduit alors un terme de dissipation $\gamma$. On considère alors le hamiltonien d’un tel système qui n’est plus hermitien :

$$\mathbb{H= \begin{bmatrix} \omega_{0} & \lambda \\ \lambda & \omega_{0} - i \frac{\gamma}{2} \end{bmatrix} \quad}$$

En étudiant ce système de deux états couplés et dissipatifs, on obtient un élargissement ou une séparation des résonances ainsi que la possibilité de battement. Dans le cadre d’un analogie quantique, on pourrait choisir $\lambda$ et $\gamma$ de sorte que les deux vecteurs propres coïncident. Ceci correspondrait à un point exceptionnel mais qui est impossible à obtenir dans le cas d’un instrument à cordes frottées. Il faut bien noter la limite de ce modèle qui ne prend en compte que l'intéraction entre deux résonances alors qu'en pratique nous pouvons nous attendre à avoir plus de deux résonances en interaction à certains endroits.

Annexe

On cherche à résoudre l'équation suivante, provenant de l'analyse de Kergomard et Chaigne³ : \begin{equation} \mathbb{M}\ddot{q}+\mathbb{C}\dot{q}+\mathbb{K}q = 0 \end{equation} \begin{equation} \nonumber \iff \left\{ \begin{array}{r c l} m_{11}\ddot{q}_1+m_{12}\ddot{q}_2+c_{11}\dot{q}_1+ k_{11}q_1 &=& 0\\ m_{21}\ddot{q}_1+m_{22}\ddot{q}_2+c_{22}\dot{q}_2+ k_{22}q_2 &=& 0\\ \end{array} \right. \end{equation} On passe en complexe pour résoudre ce système d'équations différentielles couplées. On pose : $$q_1 = q_{0_1}e^{j\omega t}\Rightarrow \dot{q}_1 = j\omega q_{0_1}e^{j\omega t} \Rightarrow\ddot{q}_1 = -\omega^2 q_{0_1}e^{j\omega t}$$ $$q_2 = q_{0_2}e^{j\omega t}\Rightarrow\dot{q}_2 = j\omega q_{0_2}e^{j\omega t}\Rightarrow\ddot{q}_2 = -\omega^2 q_{0_2}e^{j\omega t}$$ On remplace dans (3): \[ \left\{ \begin{array}{r c l} -\omega^2 m_{11}q_1 -\omega^2 m_{12}q_2+j\omega c_{11}q_1+ k_{11}q_1 &=& 0\\ -\omega^2 m_{21}q_1 -\omega^2 m_{22}q_2+ j\omega c_{22}q_2+ k_{22}q_2 &=& 0\\ \end{array} \right. \] $$ \iff \left\{ \begin{array}{r c l} (-\omega^2 m_{11}+j\omega c_{11}+ k_{11}) q_{0_1}-\omega^2 m_{12}q_{0_2} &=& 0\\ -\omega^2 m_{21}q_{0_1}+ (-\omega^2 m_{22}+ j\omega c_{22}+ k_{22})q_{0_2} &=& 0\\ \end{array} \right. $$ On a des solutions si et seulement si le déterminant est nul, soit : \begin{eqnarray}\nonumber (-\omega^2 m_{11}+j\omega c_{11}+ k_{11})(-\omega^2 m_{22}+ j\omega c_{22}+ k_{22})-(-\omega^2 m_{12})(-\omega^2 m_{21}) &=& 0\\ \nonumber \iff \omega^4 m_{11} m_{22} -\omega^2 m_{11}j\omega c_{22} -\omega^2 m_{11}k_{22} - j\omega c_{11} \omega^2 m_{22} && \\ \nonumber - \omega^2c_{11}c_{22} + j\omega c_{11}k_{22}- k_{11} \omega^2 m_{22} + k_{11} j\omega c_{22}+ k_{11}k_{22} &=& \omega^4 m_{12} m_{21} \nonumber %\iff \frac{\omega^4 m_{11} m_{22} -\omega^2 m_{11}j\omega c_{22} -\omega^2 m_{11}k_{22} - j\omega c_{11} \omega^2 m_{22} && \\ \nonumber %- \omega^2c_{11}c_{22} + j\omega c_{11}k_{22}- k_{11} \omega^2 m_{22} + k_{11} j\omega c_{22}+ k_{11}k_{22}}{m_{11} m_{22}} &=& \omega^4 \frac{m_{12} m_{21}}{m_{11} m_{22}} \end{eqnarray} On divise des deux côtés par $m_{11} m_{22}$ et on remplace $c_{11}$ et $c_{22}$ par leurs valeurs : \begin{eqnarray}\nonumber \omega^4 -2\omega^2 j\omega \zeta_B\omega_B -\omega^2\frac{ k_{22}}{m_{22}} - 2j\omega \zeta_S\omega_S \omega^2 - 4\omega^2 \zeta_S\omega_S\zeta_B\omega_B \\ \nonumber + 2 j\omega \zeta_S\omega_S\frac{ k_{22}}{m_{22}} - \frac{ k_{11}}{m_{11}} \omega^2 + 2j\omega \zeta_B\omega_B\frac{ k_{11}}{m_{11}}+ \frac{k_{11}k_{22}}{m_{11} m_{22}} &=& \omega^4 \frac{m_{12} m_{21}}{m_{11} m_{22}} \nonumber \end{eqnarray} On identifie $ \frac{ k_{22}}{m_{22}}=\omega_B^2 $ ; $ \frac{ k_{11}}{m_{11}}=\omega_S^2 $ ; $ \frac{m_{12} m_{21}}{m_{11} m_{22}} = \lambda^2 $ $$ \omega^4 -2\omega^2 j\omega \zeta_B\omega_B -\omega^2\omega_B^2 - 2j\omega \zeta_S\omega_S \omega^2 - 4\omega^2 \zeta_S\omega_S\zeta_B\omega_B + 2j\omega \zeta_S\omega_S\omega_B^2- \omega^2\omega_S^2 + 2j\omega \zeta_B\omega_B\omega_S^2+ \omega_S^2\omega_B^2 = \omega^4 \lambda^2 $$ On retrouve bien : \begin{equation} (\omega_S^2 +2 j\omega \zeta_S\omega_S -\omega^2)(\omega_B^2 +2 j\omega \zeta_B\omega_B -\omega^2) = \omega^4 \lambda^2 \nonumber \end{equation}