Analyse :
Les résonances :
Les dimensions particulières d'une pièce impliquent qu'elle possède des fréquences de résonances qui lui sont propres. Tous les modes de résonances sont toujours présents dans l'enceinte quelque soit l'excitation que l'on applique. Cependant, l'intensité avec laquelle ces modes s'exprimeront sera plus ou moins élevée en fonction des lieux où on les observe ainsi que des caractéristiques de l'excitation.
Pour illustrer ces propos, on se propose d'analyser la reponse de la boite pour une même excitation à deux positions différentes. Pour une première observation, on place le micro à un point précis de la boite, à une hauteur choisit puis une nouvelle fois, on change sa hauteur d'une distance significative afin de mesurer la même excitation en un autre point de l'espace.
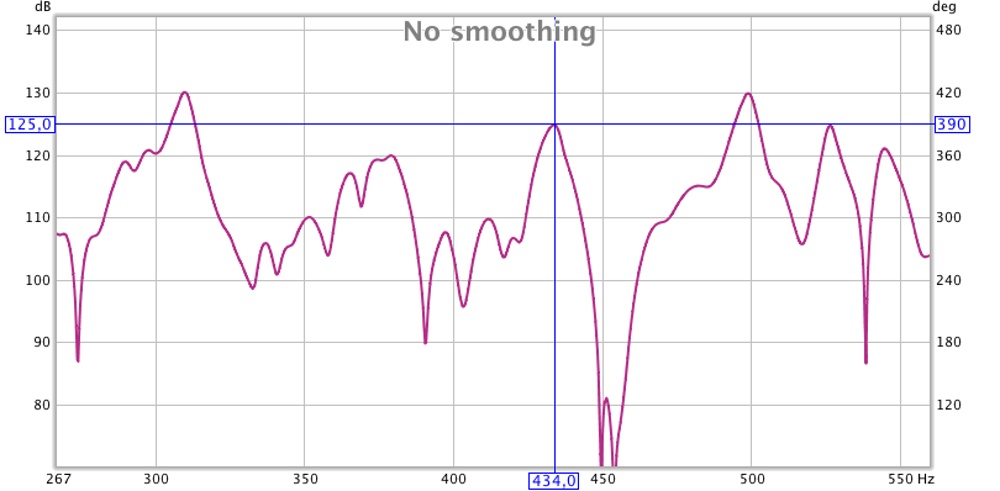
Ces deux graphiques représentent la reponse de la boite à une excitation avec la paume de la main sur la même paroi. Le signal est observé au point A successivement à 20cm puis 40cm du couvercle placé sur la face supérieur.
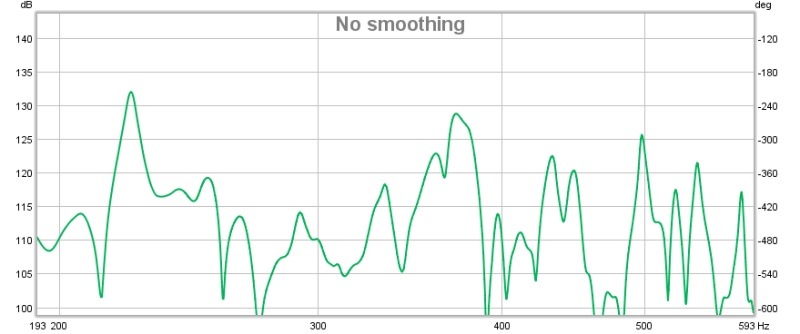
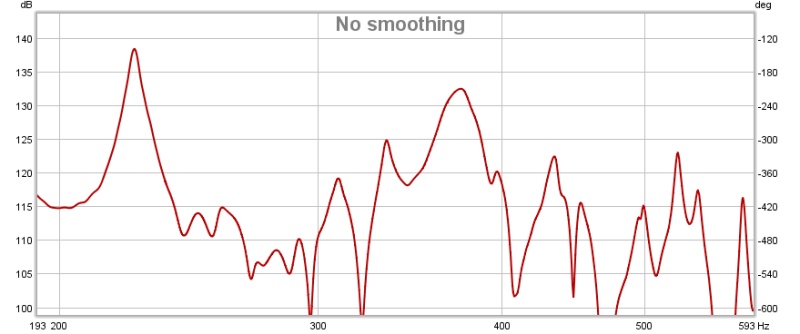
On identifie la position des différents modes grâce à la formule de la fréquence de résonance pour ensuite comparer leurs expréssions au sein de la boite.
$$f=\frac{c}{2} \sqrt{\frac{p^2}{L^2}+\frac{q^2}{W^2}+\frac{r^2}{H^2}}$$
Mode 1 (1,0,0) : 223,3 Hz ; Mode 2 (0,1,0) : 245,7 Hz ; Mode 3 (0,0,1) : 294,7 Hz
Mode 4 (1,1,0) : 325,4 Hz ; Mode 5 (1,0,1) : 363,8 Hz ; Mode 6 (0,1,1) : 383,7 Hz
Mode 7 (2,0,0) : 426,6 Hz ; Mode 8 (1,1,1) : 439,0 Hz ; Mode 9 (0,2,0) : 491,4 Hz
Mode 10 (2,1,0) : 492,3 Hz ; Mode 11 (2,0,1) : 518,5 Hz ;
On observe sur les graphiques que les fréquences à laquelle les modes s'expriment ne changent pas mais qu'il existe une différence d'intensité avec leur homologues respectifs. On remarque également que dans les deux graphiques et de manière différente, certains modes se retrouvent recouverts par leurs voisins et qu'à l'inverse, d'autres n'apparaissent quasiment pas.
Les modes s'expriment donc bien de nombreuses manières dans l'espace traduisant des résonances et un son différent. La qualité acoustique d'une salle reposera ainsi sur la façon dont vont s'exprimer ces modes et le son que l'auditeur percevra après toutes les réverbérations dans la salle.
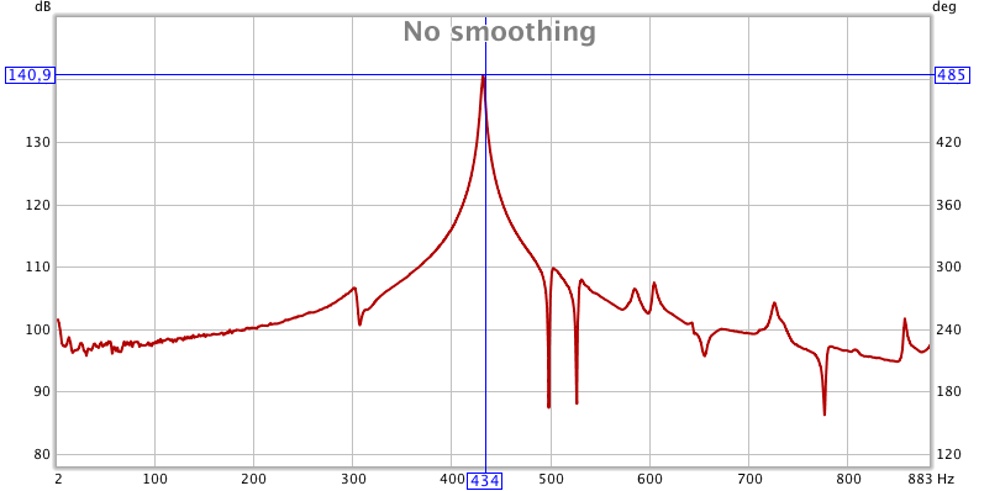
Lorsque l'on identifie les fréquences de résonances d'une salle, on peut choisir d'exciter seulement le mode correspondant à une fréquence précise. Pour cela on place une enceinte au mileu de la salle dont le signal émit ne contiendra qu'une seule fréquence celle du mode. Le spectre ne contiendra ainsi qu'une seule résonance celle du mode choisit.
On observe ce phénomène pour une resonance prise pour une réponse de la salle pour un choc avec la paume de la main. Le micro est placé au centre de la pièce, 40cm en-dessous du couvercle.
Le temps de réverbération :
Le temps de réverbération d'un signal se propageant dans un espace clos dépend de nombreux facteurs environnementaux et se trouve relié à d'autres quantités caractéristiques du signal telle que la bande passante. Comme précédement évoqué dans la partie théorie, le temps de réverbération est inversement proportionel à la bande passante, ce temps observé peut ainsi être corrélé au mode se trouvant à cette fréquence. L'observation des modes d'un signal peut donc permettre de calculer le temps de réverbération pour cette fréquence.
Au travers de plusieurs mesures éffectuées au sein de la boite, on utilisera les bandes passantes de certains modes extraits de reponses provenant d'excitations différentes. On pourra ensuite en déduire à la fréquence correspondante, quel est le temps de réverbération de notre signal et comment la nature de cette reponse engendre des temps différents.
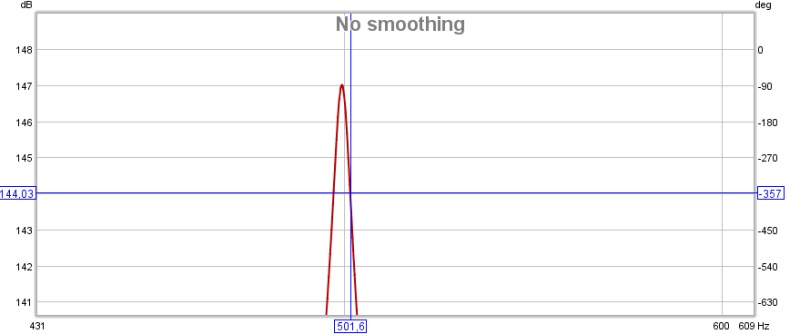
On étudie un signal relevé au point A (angle) de la boite à une hauteur de 40cm en-dessous du couvercle pour une excitation crée avec un choc de la paume de la main sur une parois externe. On choisit d'observer une résonance se trouvant proche de 500 Hz.
bande passante : 501,6 - 497,7 = 3,9 Hz
On injecte le résultat : T = 2,2 / (bande passante) = 0,564 S
la valeur théorique observé par un logiciel de traitement est T = 0,564 S
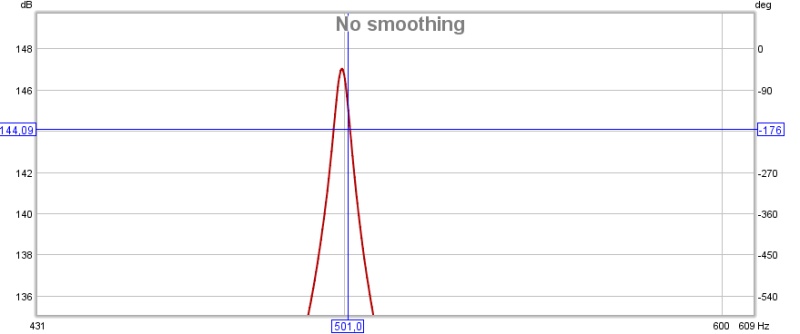
On utilise pour une autre demonstration un signal provenant d'une excitation faite par une enceinte placée au point E (centre) de la boite émettant un signal à une fréquence de 500 Hz uniquement. On observera la même raisonance que précédement (proche 500 Hz).
bande passante : 501,0 - 495,7 = 5,3 Hz
On injecte le resultat : T = 2,2 / (bande passante) = 0,415 S
la valeur expérimental observé par le logiciel de traitement est T = 0,414 S
Les valeurs des temps de réverbérations sont différents car ils proviennent d'excitations différentes cependant on peut voir dans les deux cas que les prévions faite par la formule de la bande passante sont vérifiées avec une précision satisfaisante.
Le recouvrement modal :
Le recouvrement modal traduit dans quelles proportions les modes présents dans un signal vont se rapprocher voir se chevaucher pour des fréquences basses ou élévées. Pour de basses fréquences les modes étant distinguables les uns des autres, la valeur du recouvrement est faible. A partir des premiers chevauchement de mode la valeur du recouvrement vaut un 1. On observe ainsi une croissance de ces valeurs jusqu'à dépasser 3 la fréquence de Schroeder.
Pour cette analyse on choisit d'étudier la reponse d'une salle dont 5 des 6 parois internes ont été recouvertes de carrelage afin de la rendre plus réverbérante. On choisit une excitation provenant d'une enceinte placée au milieu de la salle et qui retransmet un signal de 500 Hz, pour observer une valeur du recouvrement assez élevée. On modifie le volume interne initial de la boite afin de prendre en compte la présence de carrelage et également dans le calcul de l'aire interne.
On prend soin d'utiliser la vitesse de propagation du son correspondant à la température ambiante c = 343 m/s. On appliquera une valeur pour la bande passante relevée sur le signal de 4,7 Hz.
$$M(f)= \frac{dN(f)}{df} \Delta f = ( 4\pi V \frac{f^2}{c^3} + \frac{\pi}{2}S\frac{f}{c^2} + \frac{l}{8c} ) \Delta f$$
On calcule le volume interne de la boite et la surface intérieur total :
$$ V = 0,704*0,683*0,578 = 0,28 m^3$$
$$ S = 2*(0,704*0,683 + 0,704*0,578 + 0,683*0,578) = 2,57 m^2$$
$$l = 4*(0,704 + 0,683 +0,578) = 7.86 m $$
On obteint : M(500 Hz) = 0.18
Une estimation des resultats à des fréquences plus élevées comme M(1000)= 0,55 et à M(2000)= 1,9 permet de valider notre valeur et d'estimer un recouvrement dépassant 3 pour des fréquences proches de 2500 Hz.
Ce calcule permet ainsi vérifier jusqu'à quelle valeur l'identification des modes sur le spectre d'une réponse est possible et quantifier précisement à quelle fréquence l'approche probalistique devient nécéssaire dans notre boite.