Nous reprenons les équations du Modèle de l'Hydrodynamique dans cette partie. Nous allons ensuite appliquer nos nouvelles variables en simplifiant au maximum nos équations.

Nous verrons ce que ces perturbations provoquent sur notre système.

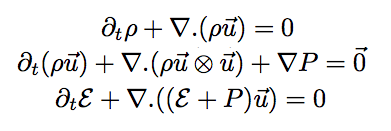
Changement de variables et simplification

La première étape est de passer de nos variables à l'équilibre à celle avec une perturbation. Par exemple : P → P₀ + P₁

De plus comme l'équation est conservative (le second membre est nul), on va pouvoir grandement simplifier.

Nous ne gardons que les termes à l'ordre 1. On néglige les termes d'ordre supérieurs pour les variables perturbatives.

$(\partial_{t} + \vec{u_{0}}.\nabla)\rho_{1} + \rho_{0}\nabla.\vec{u_{1}} = 0$

$\rho_{0}(\partial_{t} + \vec{u_{0}}.\nabla)\vec{u_{1}} + \nabla P_{1} = \vec{0}$

$(\partial_{t} + \vec{u_{0}}.\nabla)P_{1} + \gamma P_{0} \nabla.\vec{u_{1}} = 0$

Maintenant, on combine ces équations pour en obtenir qu'une seule. Les étapes de calculs ne sont pas trop difficiles. On pose : c² = γP₀/ρ₀

Remarque : c est dimensionnellement une vitesse et correspond ici à la vitesse d'une onde acoustique.

$(\partial_{t} + \vec{u_{0}}.\nabla)^2 \vec{u_{1}} + c^2 \nabla(\nabla.\vec{u_{1}}) = \vec{0}$

Passage en notation ondulatoire

Nous avons visiblement à faire avec une relation de dispersion. Pour cela, on considère que la perturbation de vitesse est sous une forme d'onde. On écrit donc en notation complexe chaque variable (à droite première ligne).

Les opérateurs de dérivée temporelle et de divergence. On simplifie pour avoir la forme d'une équation propre (à droite seconde ligne).

$\vec{u_{1}}(r,t) = \sum_{k} e^{i(\vec{k}.\vec{r} - \omega t)}\hat{u}_{k}$

$[(\omega - \vec{u_{0}}.\vec{k})^2 I - c^2\vec{k}\vec{k}].\hat{u} = 0$

Conditions

On se place dans le cas où u₀ est nul et le vecteur d'onde est selon e_z. On considère que le fluide a une vitesse nulle sans la perturbation et l'onde de vitesse se propage selon un axe e_z.

On note à droite les équations sur chaque axe.

$\vec{e_{x}} : \omega^2 \hat{u_{x}} = 0$

$\vec{e_{y}} : \omega^2 \hat{u_{y}} = 0$

$\vec{e_{z}} : (\omega^2 - c^2 k^2 ) \hat{u_{z}} = 0$

Solutions et analyse

Solution 1

La première possibilité est que :
   • ω = ± kc
   • u_x = u_y = 0
   • u_z quelconque

On remarque que la vitesse est polarisée dans le sens de propagation de l'onde : l'onde est Longitudinale.
Donc : k.u ≠ 0 et donc la divergence de la vitesse est nulle : l'onde est Compressible.

Il s'agit de l'onde acoustique que l'on connait. Elle est matérielle et représente des détentes ou des chocs.

Solution 2

La seconde possibilité est que :
   • ω = 0
   • u_z = 0
   • u_x, u_y quelconque

On remarque que la vitesse est polarisée orthogonalement au sens de propagation de l'onde et donc que k.u = 0. La divergence de la vitesse est nulle.

L'onde est Transverse Incompressible.

Perturbation du modèle de la MHD →