Pour écrire les équations de conservation pour un fluide, nous devons faire des hypothèses. On considère un système à l'équilibre et un fluide parfait sans forces volumiques.
Lors de l'écoulement d'un tel fluide, la masse (ou la masse volumique), la quantité de mouvement et l'énergie (ou la pression) sont conservées.
On note u la vitesse du fluide, ρ la masse volumique, P la pression et ε l'énergie totale.
Conservation de la masse
Notre système est à l'équilibre. Aucune masse de fluide ne sort ou n'entre dans le système.
L'équation de conservation de la masse est donnée à droite.
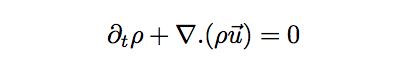
Conservation de la quantité de mouvement
Le fluide n'est soumis à aucune force volumique donc la quantité de mouvement est conservée.
De plus, le fluide est parfait donc en utilisant l'équation d'Euler(équation 11),
on peut trouver une forme simple de cette équation de conservation.
L'équation de conservation de la quantité de mouvement est donnée à droite.
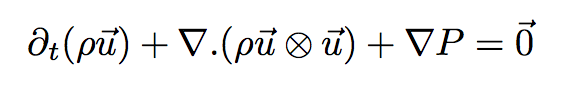
Conservation de l'énergie
Le fluide est considéré non visqueux. On néglige donc les pertes d'énergies. L'équation d'Euler
nous permet d'écrire une équation sur l'énergie cinétique. Puis, l'énergie totale s'écrit comme la somme
de l'énergie cinétique et l'énergie totale.
L'équation de conservation de la quantité de mouvement est donnée à droite.
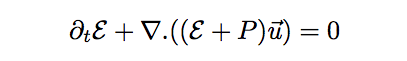
Ces équations ci-dessus sont la base de tous nos calculs. Nous pouvons déterminer le modèle de la MHD et le modèle bi-fluide en partant de ces équations.
