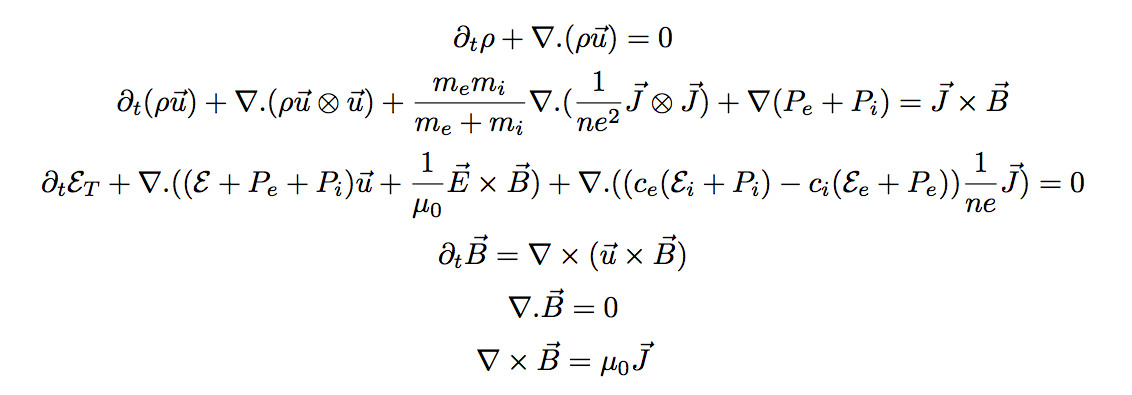Pour obtenir le modèle final, nous devons combiner les 2 précédents. Notre système sera bien celui de 2 fluides traversés par
un champ magnétique.
Le fait que deux fluides différents soient soumis tous deux à un champ magnétique va entraîner un courant de charges au sein du tokamak.
Nous allons utiliser maintenant l'hypothèse de quasi neutralité pour simplifier nos équations.
Quasi neutralité et courant de charges
L'hypothèse que quasi neutralité nous impose que la densité de charges est nulle.
Soit : ρ' = neqe + niqi = 0
Dans les tokamaks, nous avons des isotopes de l'hydrogène donc les ions sont simplement des protons.
Or, qproton = −qelectron,
donc nécessairement : n = ne = ni
En notant la proportion de masse pour chaque espèce cα = mα/(mi + me), on peut écrire la vitesse comme :
u = ceue + ciui
Comme les vitesses des 2 fluides sont différentes, un courant J est engendré tel que :
J = ne(ui-ue) où e est la charge élémentaire.
On peut donc écrire les vitesses de chaque fluide (à droite).
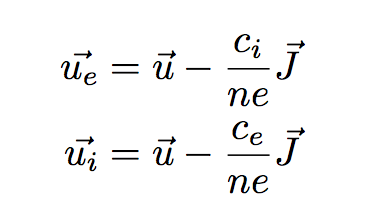
modèle final
Nous avons tout ce dont on a besoin pour écrire le modèle. Il suffit de combiner les équations du modèle MHD avec celles du modèle bi-fluide en prenant en compte les nouveaux paramètres énoncés ci-dessus.