Pour trouver les équations de conservation de la Magnétohydrodynamique, on considère un fluide chargé traversé par un champ magnétique.
C'est par exemple le cas du Soleil.
On a besoin d'autres équations pour décrire ce système.
Nous avons besoin d'informations sur le champ magnétique et d'hypothèses supplémentaires.
On considère que le fluide est:
• Non relativiste
• Infiniement conducteur
De plus, on considère que les effets magnétiques prédominent.
équations de maxwell
Le champ magnétique est désormais présent. Nous avons donc besoin des équations de Maxwell
provenant de l'électromagnétisme (à droite).
Nos hypothèses nous servent à simplifier ces équations.
• Comme le fluide est non relativiste, E/c² est négligeable.
Nous écrirons les équations simplifiées lors du modèle complet de la MHD.
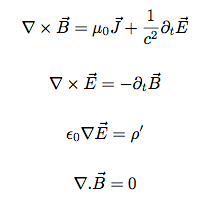
Modification du modèle de l'hydrodynamique
Le champ magnétique n'influence pas toutes les équations de l'Hydrodynamique.
L'équation de la conservation de la masse est inchangée. Le champ magnétique n'ajoute pas de masse au système.
On a remarqué que l'équation sur la quantité de mouvement a comme dimension la dimension d'une force.
Or le champ magnétique exerce la Force de Laplace en considérant que les effets magnétiques prédominent.
Soit : F = J × B
Pour l'équation sur l'énergie, on doit prendre en compte l'effet joule et le flux du vecteur de Poynting.
On doit ajouter à cette équation 2 termes : J.E et ∇.Π
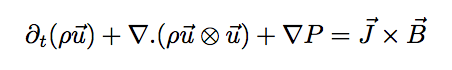
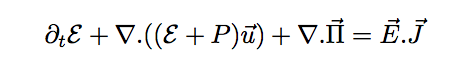
MHD idéale : modèle complet
Nous avons toutes les équations pour écrire le modèle. Cependant, une hypothèse n'a pas été utilisée : celle du fluide infiniment conducteur.
Il s'agit en fait d'une condition importante. Sans elle, on se place dans le cas de la MHD résistive. Avec cette condition, il s'agit du modèle de la
MDH idéale. On s'occupe du modèle idéal.
Comme le fluide est infiniement conducteur,à partir de l'équation du courant, on peut déduire
que : E = -u × B
On a donc le modèle complet de la MHD, sur la droite.
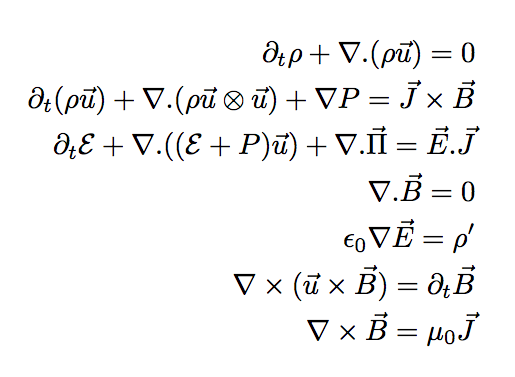
Le modèle de la MHD idéale est établi. Pour arriver au modèle final, on a besoin de considérer que l'on a 2 fluides différents. Nous avons pas besoin de ce modèle pour trouver le modèle bi-fluide.
