Nous reprenons les équations du Modèle de la MHD.
Au lieu de travailler
sur le modèle qu'on a explicité à la fin de la page sur ce modèle, nous décidons de regarder un autre
système. Il s'agit simplement d'un couplage entre équations de l'hydrodynamique et équations de Maxwell.
Avec quelques identités vectorielles et en ne gardant comme variable que ρ, u, P et B,
on obtient le système ci contre.
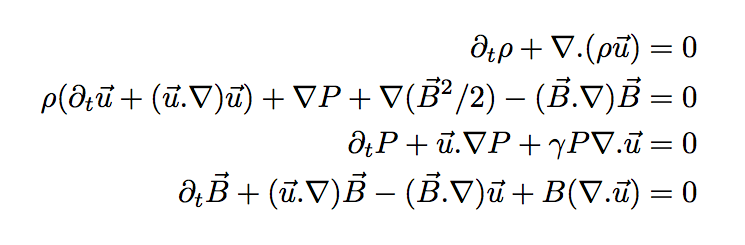
Changement de variables et simplification
Comme pour l'hydrodynamique, on remplace la variable à l'équilibre X par X0 + X1.
On ne change pas nos conditions qui sont de ne garder que l'ordre 1 pour les variables perturbées.
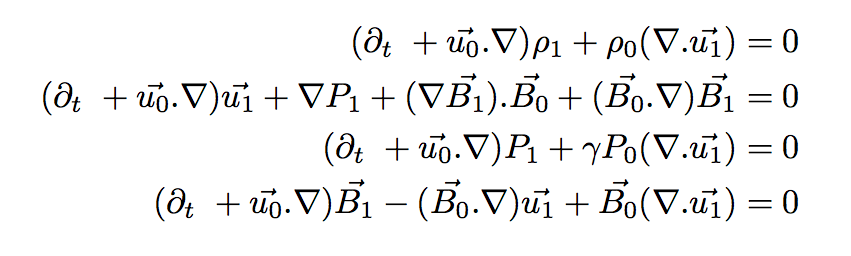
Cette fois ci, il est plus difficile de combiner les équations. On décide de travailler avec l'énergie plutôt que la pression
dans ce cas. Nous utilisons la loi d'état énoncée lors de l'introduction aux perturbations.
On pose que la vitesse de base est nulle, soit : u0 = 0.
On ajoute une condition, celle que le flux du champ magnétique de base B0 doit être nul.
$\partial_{t}\rho_{1} + \rho_{0}\nabla.\vec{u_{1}} = 0$
$\rho_{0}\partial_{t}\vec{u_{1}}+(\gamma-1)[\rho_{0}\nabla\epsilon_{1} + \epsilon_{0}\nabla\rho_{1}]$
$+ (\nabla \vec{B_{1}}).\vec{B_{0}} - (\vec{B_{0}}.\nabla)\vec{B_{1}}=0$
$\partial_{t}\epsilon_{1} + (\gamma-1)\epsilon_{0}\nabla.\vec{u_{1}} = 0$
$\partial_{t}\vec{B_{1}} + \vec{B_{0}}\nabla.\vec{u_{1}} - \vec{B_{0}}.\nabla(\vec{u_{1}}) = 0$
$\nabla.\vec{B_{0}} = 0$
Maintenant, on remplace des termes constants. Nous connaissons déjà la vitesse de l'onde acoustique c.
On introduit une nouvelle vitesse qui est la Vitesse vectorielle d'Alfvén : b² = B0²/ρ0.
Cette vitesse est vectorielle.
De plus, on adimensionnalise les variables. On la note avec le symbole tilde.
$\gamma\partial_{t}\tilde{\rho} + c\nabla.\tilde{\vec{u}} = 0$
$\partial_{t}\tilde{\vec{u}} + c\nabla\tilde{\rho} + c\nabla\tilde{\epsilon} + (\nabla \tilde{\vec{B}}).\vec{b} - \vec{b}.\nabla\tilde{\vec{B}}=0$
$\frac{\gamma}{\gamma-1}\partial_{t}\tilde{\epsilon} + c\nabla.\tilde{\vec{u}} = 0$
$\partial_{t}\tilde{\vec{B}} + \vec{b}\nabla.\tilde{\vec{u}} - \vec{b}.\nabla(\tilde{\vec{u}}) = 0$
$\nabla.\tilde{\vec{B}} = 0$
Passage en notation ondulatoire
De la même manière que précédemment, nous écrivons sous forme complexe nos variables. Nous n'avons pas pu les
simplifier, donc nous avons 4 variables. Or, 2 d'entre elles sont vectorielles donc nous avons un système à 8
inconnues. Ceci complique grandement le problème.
Ecrivons d'abord nos nouvelles variables.
$\tilde{\rho}(r,t) = e^{i(\vec{k}.\vec{r} - \omega t)}\hat{\rho}$
$\tilde{\vec{u}}(r,t) = \sum_{k} e^{i(\vec{k}.\vec{r} - \omega t)}\hat{u}_{k}$
$\tilde{\epsilon}(r,t) = e^{i(\vec{k}.\vec{r} - \omega t)}\hat{\epsilon}$
$\tilde{\vec{B}}(r,t) = \sum_{k} e^{i(\vec{k}.\vec{r} - \omega t)}\hat{B}_{k}$
Conditions
Nous pouvons maintenant simplifier nos équations avec cette notation.
De plus, nous allons poser des condtions :
• b est selon ez
• k = (k⊥, 0, k=)
A droite, vous avez la notation sous forme d'un système d'équations.
Ci-dessous, ce système est sour forme matricielle. On voit bien qu'il s'agit d'une équation aux valeurs propres ω.
$\omega\gamma\hat{\rho} = ck_{\perp}\hat{u_{x}} + ck_{=}\hat{u_{z}}$
$\omega\hat{u_{x}} = ck_{\perp}\hat{\rho} + ck_{\perp}\hat{\epsilon} - bk_{=}\hat{B_{x}} + bk_{\perp}\hat{B_{z}} $
$\omega\hat{u_{y}} = - bk_{=}\hat{B_{y}}$
$\omega\hat{u_{z}} = ck_{=}\hat{\rho} + ck_{=}\hat{\epsilon}$
$\frac{\gamma}{\gamma - 1}\omega\hat{\epsilon} = ck_{\perp}\hat{u_{x}} + ck_{=}\hat{u_{z}}$
$\omega\hat{B_{x}} = - bk_{=}\hat{u_{x}}$
$\omega\hat{B_{y}} = - bk_{=}\hat{u_{y}}$
$\omega\hat{B_{z}} = bk_{\perp}\hat{u_{x}}$
$\begin{pmatrix} 0 & ck_{\perp} & 0 & ck_{=} & 0 & 0 & 0 & 0 \\ ck_{\perp} & 0 & 0 & 0 & ck_{\perp} & - bk_{=} & 0 & bk_{\perp} \\ 0 & 0 & 0 & 0 & 0 & 0 & - bk_{=} & 0 \\ ck_{=} & 0 & 0 & 0 & ck_{=} & 0 & 0 & 0 \\ 0 & ck_{\perp} & 0 & ck_{=} & 0 & 0 & 0 & 0 \\ 0 & - bk_{=} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & - bk_{=} & 0 & 0 & 0 & 0 & 0 \\ 0 & bk_{\perp} & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}$ $\begin{pmatrix} \hat{\rho} \\ \hat{u_{x}} \\ \hat{u_{y}} \\ \hat{u_{z}} \\ \hat{\epsilon} \\ \hat{B_{x}} \\ \hat{B_{y}} \\ \hat{B_{z}} \end{pmatrix} = \omega \begin{pmatrix} \gamma\hat{\rho} \\ \hat{u_{x}} \\ \hat{u_{y}} \\ \hat{u_{z}} \\ \frac{\gamma}{\gamma - 1}\hat{\epsilon} \\ \hat{B_{x}} \\ \hat{B_{y}} \\ \hat{B_{z}} \end{pmatrix}$
Relation de dispersion
Nous devons calculer le déterminant de cette matrice 8x8 pour déduire la relation de dispersion puis les valeurs propres du système.
Pour cela, on modifie la matrice pour avoir le même vecteur à droite et à gauche. On utilise une relation non triviale pour modifier l'équation. Nous passons les détails de calculs car le calcul du déterminant est long et fastidieux.
Nous avons obtenu la relation à droite.
On note k² = k⊥² + k=².
$\omega^2 (\omega^2 - b^2 k_{=}^2 ) [\omega^2 (\omega^2 - k^2 (b^2 + c^2)) + k_{=}^2 k^2 b^2 c^2] = 0$
Valeurs propres
Il suffit maintenant de trouver les différentes pulsations ω qui sont solutions de la relation de dispersion.
L'équation est de degré 8, donc on doit avoir 8 valeurs propres différentes.
Remarque : La valeur propre ω = 0 est double.
La première pulsation ω correspond à l'Onde Acoustique déja présente lorsqu'on perturbe le modèle hydrodynamique.
ωA correspond à l'Onde d'Alfvén. Hannes Alfvén a reçu le Prix Nobel en 1970 notamment grâce à la découverte de cette onde.
La vitesse b est appelée la Vitesse d'Alfvén.
Les pulstions ωS et ωF correspondent à des Ondes Lentes ("slow") et des Ondes Rapides ("fast").
Une perturbation de notre système génère 4 ondes différentes. Nous allons maintenant déterminer les vecteurs propres pour les 3 dernières afin de déterminer leur nature.
$\omega = 0$
$\omega_{A} = \pm bk_{=}$
$\omega_{S} = \pm k \sqrt{\frac{b^2 + c^2}{2}(1 - \sqrt{1 - \frac{4k_{=}^2 b^2 c^2}{k^2 (b^2 + c^2)^2}})}$
$\omega_{F} = \pm k \sqrt{\frac{b^2 + c^2}{2}(1 + \sqrt{1 - \frac{4k_{=}^2 b^2 c^2}{k^2 (b^2 + c^2)^2}})}$
Vecteurs propres
Nous reprenons l'équation matricielle ou le système dans la partie Conditions et nous remplaçons
ω par ωA, ωS et ωF.
Nous passons les étapes de calculs qui n'ont rien de difficile mais qui demandent du temps. Comme pour l'hydrodynamique,
nous allons déterminer la polarisation et la compressibilité de l'onde.
Onde d'Alfvén
$\hat{\rho} = \hat{\epsilon} = 0$
$\hat{u_{x}} = \hat{u_{z}} = 0 ; \hat{u_{y}} \ne 0$
$\hat{B_{x}} = \hat{B_{z}} = 0 ; \hat{B_{y}} \ne 0$
La densité et donc l'énergie ne change pas, l'onde est Incompressible.
On peut le voir en calculant la divergence de la vitesse sachant que : k = (k⊥, 0, k=)
De plus, la vitesse est orientée orthogonalement au vecteur d'onde. L'onde est donc Transversale.
Cette onde permet de faire osciller le champ magnétique. Elle est particulière au domaine de la MHD pour un plasma.
Ondes Lentes et rapides
$\hat{\rho} + \hat{\epsilon} = \frac{\omega_{S,F}}{ck_{=}}\hat{u_{x}}$
$\hat{u_{z}} = \frac{k_{=}\alpha_{S,F}}{k_{\perp}}\hat{u_{x}} ; \hat{u_{y}} = 0$
$\hat{B_{x}} = -\frac{bk_{=}}{\omega_{S,F}}; \hat{B_{z}} = \frac{bk_{\perp}}{\omega_{S,F}}; \hat{B_{y}} = 0$
$\alpha_{S,F} = 1 - \frac{k^2 b^2}{\omega_{S,F}}$
On remarque que la densité varie. Ces ondes sont Compressibles.
De plus, les ondes sont polarisées selon la direction de propagation, comme pour l'onde acoustiques.
Elles sont Longitudinales.
Les ondes rapides et lentes ont les mêmes caractéristiques que l'onde acoustique mais elles ont le dépendance
du champ magnétique. On les appelle les Ondes Magnétoacoustiques..