VotreSite.Com

Annexe
Annexe 1
Annexe 2 : Developpement de Taylor et passage en série de Fourier
On se restreint au cas où la fonction phi(y) n'est différente de zéro que sur une région finie.
On va chercher à faire apparaître les moments de la fonction Φ(y).
Développement de Taylor de U(y+x) au voisinage de x :
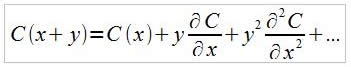
Pour y petit , on a :
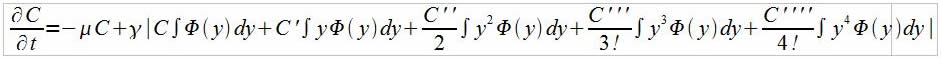
Avec
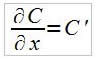
On choisit de s'arrêter à l'ordre 4.
Définition d'un moment d'ordre quelconque n : ![]()
D'où :
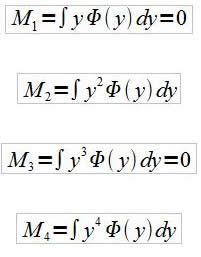
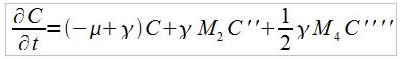
De part notre hypothèse de parité, les moments d'ordre 1et 3 sont nuls.
On fait la transformée de Fourrier.
La transformée de Fourier est analogue à l'opération de diagonalisation dans l'espace.
On obtient alors :
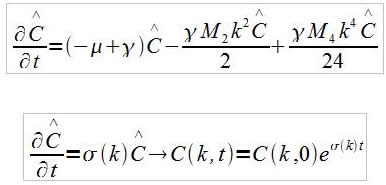
Annexe 3
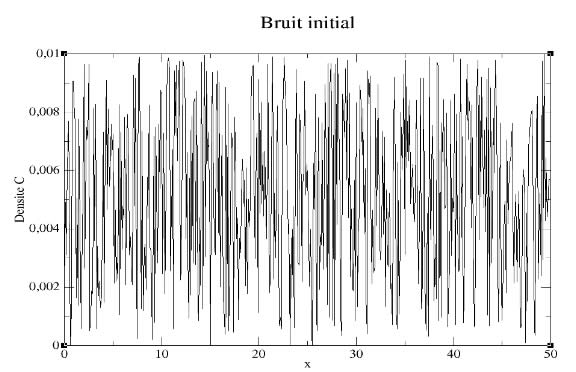
Annexe 4
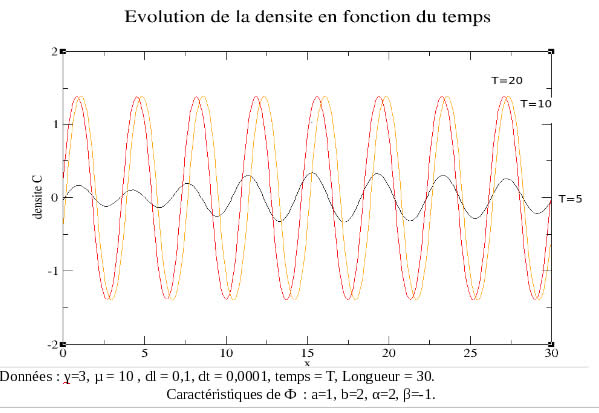
Annexe 5