VotreSite.Com

Modélisation mathématique
Le problème de croissance et d'auto-organisation de végétaux se décrit à partir d'équations différentielles. Il s'agit de transcrire la notion d'influence et de compétition qu'ont les végétaux les uns sur les autres.
Pour ce faire, il est nécessaire de présenter les parties indispensables qui traduisent des différents termes d'une équation de modélisation.
1.Taux de croissance
Le premier terme concerne la partie de croissance des végétaux sans tenir compte des interactions avec les autres végétaux.
L'expression contient des taux constants de natalité et de mortalité de végétaux.
![]()
avec :
C : densité surfacique végétale
a : taux de natalité.
b : taux de mortalité
µ = (b-a) : taux de croissance
C'est un modèle restreint utilisable sur un temps très court et sur une population réduite d'individus.
La solution de cette équation s'écrit :
![]()
Avec ce modèle, la fonction C(t) « explose » ou tend vers zéro.
Nous devons donc prendre en compte d'autres influences pour saturer et décrire au mieux les influences entre les individus du modèle d'auto-organisation biologique.
2.L'influence des proches voisins
Il faut maintenant définir la tendance qu'ont les éléments du système à influer les uns sur les autres. La fonction caractéristique Φ(s') décrivant l'influence locale des végétaux est définie ici.
Nous souhaitons introduire les rétroactions positives et négatives entre les végétaux pour tester l'influence du phénomène.
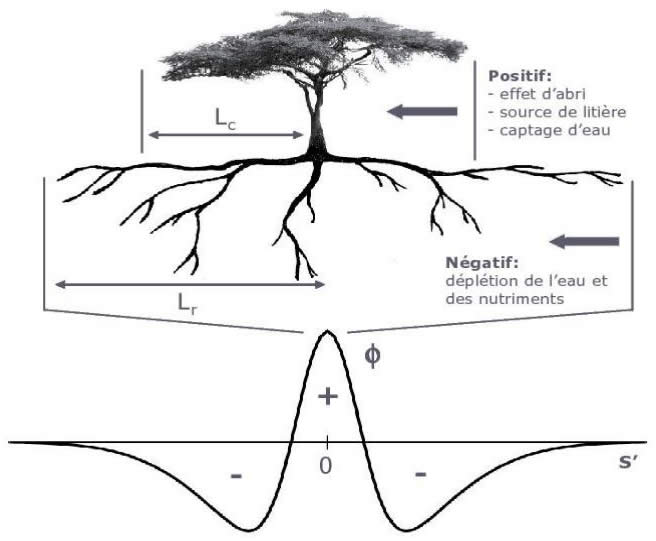
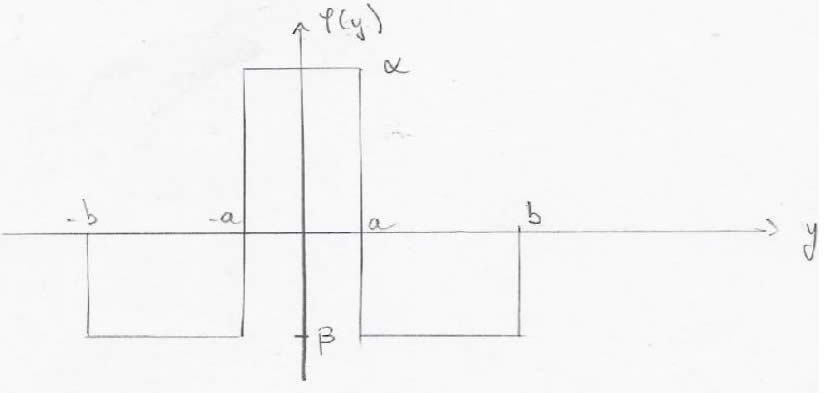
Figure : Modèle de Lefever-Lejeune montrant le potentiel d'interaction spatiale.
On crée une fonction phi de la forme ci-dessus en se basant sur les phénomènes biologiques décrits précédemment avec une action bénéfique proche de la plante concernée et une action négative à plus grande distance.
On suppose Φ(-y)=Φ(y) : Φ(y) est une fonction paire.
Etude de la partie lineaire de l'équation différentielle aux derivées partielles: influence des voisins.
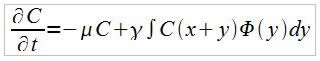
Cette équation traite de l'évolution de la densité de couvert végétal en fonction du temps prenant en compte la croissance de la population et l'effet des « voisins » sur un intervalle d'espace donné.
Pour traiter cette fonction, il est nécessaire d'introduire les moments d'ordre 1 à 4 pour la fonction Φ(y) et de passer l'équation en série de Fourier pour étudier les solutions.
Le calcul des moments et du passage en série de Fourier est fourni
Les résultats qui en ressortent sont les suivants :
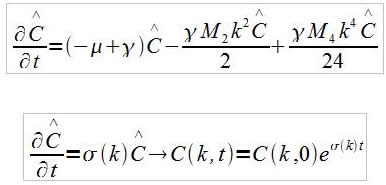
Les signes des moments d'ordre 2 et 4 vont influer sur la forme du tracé de σ(k).
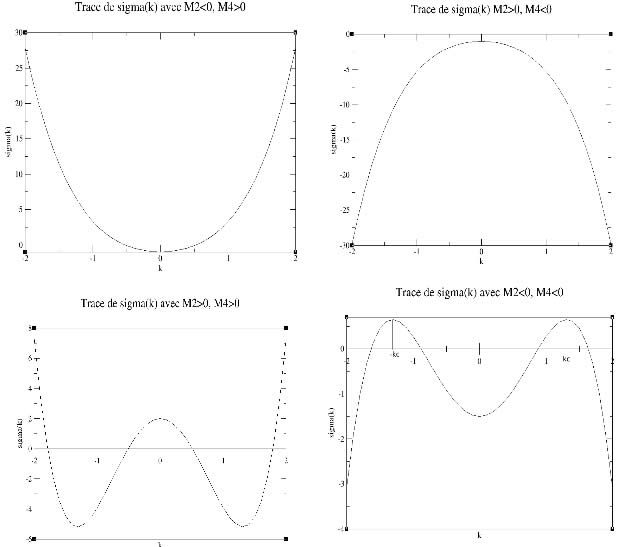
Soient respectivement 1, 2, 3, 4 ces graphiques de gauche à droite.
Le choix du signe de M2 et de M4 doit nous permettre de faire apparaître une seule longueur caractéristique associée à un mode de Fourier instable.
On choisit M2<0 et M4<0 car le graphique 4 est le seul à présenter un seul mode de Fourier instable (en positif).
On choisit donc un σ(k) de la forme :
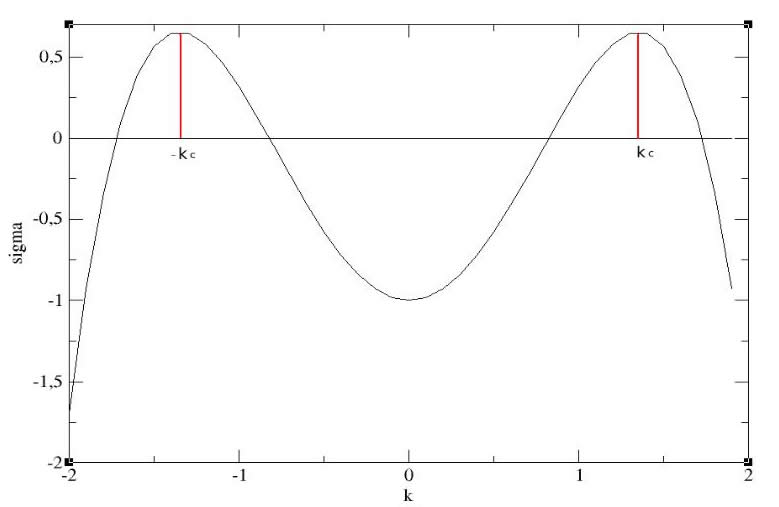
Soit kc le nombre d'onde critique associé à la longueur d'onde critique.
Les composantes de la transformée de Fourier de C qui vérifient σ(k)<0 sont toutes amorties
au cours du temps.
Il reste seulement les valeurs voisines de kc (on raisonne uniquement en positif pour la valeur de k).
Au bout d'un certain temps, dans l'espace réel, la longueur d'onde associée à kc va apparaître.
Les modes de Fourier voisins de kc sont en compétition ; souvent kc, la valeur la plus instable, l'emporte.
Calcul théorique de kc
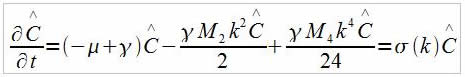
Ce qui nous donne :
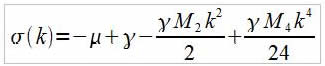
En kc, la dérivée de σ(k) par rapport à k est nulle d'où :
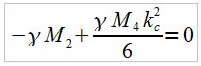
Donc
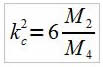
Pour des raisons de simplicité, nous avons utilisé dans un premier temps comme fonction phi la fonction porte suivante qui répond aux conditions sur les moments :
Dans cette fonction, on a bien M2<0, M4<0 tels que :
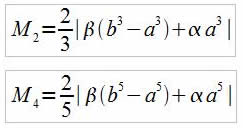
Avec 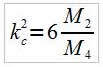
on a 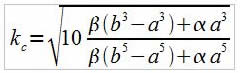
Pour cette valeur de kc, on a apparition d’une structure périodique de longueur d'onde :
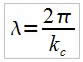
Et on obtient une valeur théorique de kc avec les paramètres de Φ(y) : a=1, b=2, α=2, β=-1:
kc = 1,31
3.Terme de saturation
Il est nécessaire de bloquer la croissance du couvert végétal lorsque celle ci devient trop importante. Cette saturation est réalisée grâce aux termes non linéaires, les premiers sont C² et C3.
Le terme quadratique C² ne sature la croissance de l'instabilité que lorsque C>0.
Le signe de C n'a pas d'importance dans notre modélisation, seul compte le fait que C est différent de zéro ou pas.
Pour ne pas etre génés par le problème de signe, on va saturer l'instabilité avec C3.
4.Equation finale
Notre système est décrit par une équation différentielle de la forme:
![]()
avec :
C²(x): densité surfacique de végétaux au point x.
dC/dt : évolution du couvert végétal en fonction du temps.
(-μ+γ) : taux de croissance en l'absence de couplage.
Φ(y) : fonction décrivant l'influence de la végétation située en (x+y) sur la végétation en x.
C³ : terme non linéaire.
γ: facteur caractéristique d'interaction entre les végétaux