Modélisation numérique

 

Il s’agit dans la partie informatique de vérifier que l’influence d’une plante sur ses voisines telle qu’elle a été décrite auparavant permet l’apparition des patterns périodiques étudiées.

Nous nous sommes servis du langage de programmation C afin de simuler l’apparition des longueurs d’ondes en 1D. Il s’agissait en fait de vérifier que le modèle mathématique était suffisamment complet pour représenter le phénomène de la brousse tigrée. En l’occurrence nous nous sommes concentrés sur le phénomène particulier de périodisation de la végétation et non sur celui de la forme des patterns qui requiert une approche en 2D.

A partir d’une densité de végétation initiale le programme calcule une densité au bout d’un temps t sur une portion d’espace prédéterminée.

En ce qui concerne les bords, nous avons fait le choix de conditions aux limites périodiques.

Quand à la dérivée de la densité, elle est calculée à partir de la formule :


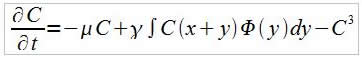
1 Notations

Soit C la densité, et dtC sa dérivée par rapport au temps. Ce sont tous deux des vecteurs de la taille de l’espace discrétisé (divisé par le pas d’espace), plus les bords nécessaires aux conditions aux limites. On retrouve aussi les vecteurs C1 et C2 dans le programme. De mêmes tailles que C et dtC, ce sont des variables intermédiaires utilisés dans le programme.

2 Subroutines utilisées

Initialisation : initialisation des diverses constantes utilisées par la suite.

Allocations : allocations des 4 vecteurs principaux, C, C1, C2 et dtC.

Libération : libération de ces mêmes vecteurs.

Phi : définition de la fonction poids en fonction de la variable d’espace.

Integ : calcul de ∫Φ(y)C1(x+y)dy par une méthode des trapèzes.

Conditions limites : Par soucis d’optimisation, les calculs du programme ne sont effectués que sur la partie des vecteurs représentant l’espace. Cette routine sert à mettre à jour les bords des conditions aux limites.

Dtc : calcul du vecteur dtC en fonction de C1, via la formule ci-dessus.

Runge-Kutta : utilisation de la méthode de Runge-Kutta afin d’estimer C pour le pas de temps suivant.

Boucle_temps_1 : Cette subroutine regroupe l’initialisation de C par un bruit de fond aléatoire suivie de la boucle de temps permettant l’évolution du programme.

Boucle_temps_2 : Même subroutine que la précédente, à la différence que l’initialisation se fait à partir d’une densité calculé précédemment.

3 Algorithme

-Choix d’un bruit de fond comme densité de départ, ou d’une densité calculée auparavant.

-Boucle sur le temps

-Boucle sur l’espace

-Etape 1 de la méthode de Runge-Kutta

-Fin de la boucle sur l’espace

-Boucle sur l’espace

-Etape 2 de la méthode de Runge-Kutta

-Fin de la boucle sur l’espace

-Boucle sur l’espace

-Etape 3 de la méthode de Runge-Kutta

-Fin de la boucle sur l’espace

-Boucle sur l’espace

-Etape 4 de la méthode de Runge-Kutta

-Fin de la boucle sur l’espace

-Fin de la boucle sur le temps

-Ecriture du C final dans un fichier lisible.

Bibliothèques utilisées :

Les bibliothèques utilisées, sont des bibliothèques courantes, stdio.h, stdlib.h, time.h et math.h.

4 Limites du programme

Les pas d’espace et de temps sont variables, toutefois, certaines valeurs ne permettent pas le fonctionnement du programme.
Sur la même base qui a été développée dans la partie mathématique, on rappelle l'équation différentielle qui régit l'auto-organisation végétale :


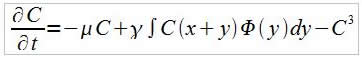
On avait :

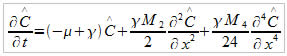
Le troisième terme de l'équation est nécessaire à la stabilisation de l'instabilité, on veut donc :

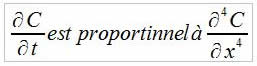
D'où dt de l'ordre de dx à la puissance 4

Les conditions aux limites périodiques imposent un nombre entier de périodes dans l’intervalle d’espace. Il faut donc que l’intervalle soit plus grand que la longueur d’onde.

Pour la même raison, il faut un intervalle beaucoup plus grand que la longueur pour obtenir un résultat précis, en effet le programme sélectionne un nombre de périodes entier, et plus on a de périodes, moins l'arrondit influe sur la précision du calcul.

Toutefois, pour pouvoir prévoir une longueur d’onde physique, il faut connaitre les constantes biologiques associées ; autant a et b sont facilement accessibles, autant α et β sont plus difficiles à définir.
Pour les déterminer, il faudrait probablement fournir un travail d'investigation empirique.
On peut d’ailleurs supposer que ces constantes sont assez complexes dans la mesure où elles doivent varier en fonction de paramètres nombreux et pas forcement homogènes comme la nature du sol, la pluviométrie, la nature de la végétation etc...

Le programme sert uniquement à montrer que les hypothèses biologiques de départ sont suffisantes pour expliquer le phénomène d’apparition de la brousse tigrée.

Obtention de la longueur d’onde recherchée:

La longueur d’onde ou le nombre d’onde ne sont pas donnés directement par le programme.

Les résultats sont écrits dans un fichier de données qui peut être converti en graphique via un logiciel comme xmgrace. Il faut ensuite mesurer le nombre de périodes contenus dans l’intervalle d’espace considéré, on notera l’intervalle d’espace longueur et le nombre de périodes N.

On obtient ensuite le nombre d’onde k ou la longueur d’onde λ de la manière suivante :

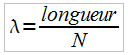
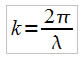
5 Résultats

L'état initial est défini par un bruit pris aléatoirement dont les valeurs sont comprises entre 0 et 0,01. (Cf annexe)

Le programme nous permet bien d’observer l’apparition spontannée de longueurs d’ondes sous la forme de courbes sinusoïdales.


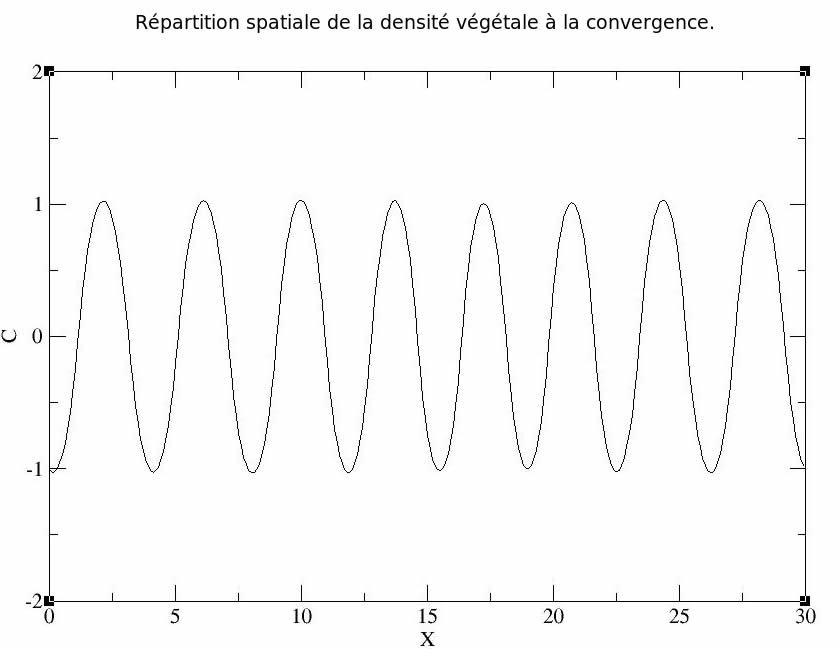
Les longueurs d’ondes obtenues ont le même ordre de grandeur que celles qui ont été calculé théoriquement.Résultat obtenu pour μ = 3 , γ = 1, dt = 0,0001, dl = 0,1, longueur = 30, temps_max = 15.

On trouve kexpérimental = 1,68.

Et kthéorique = 1,31.

L'ordre de grandeur est respecté pour chaque résultat théorique et expérimental.

On remarque sur cette feuille de résultat une différence d'à peu près 30% entre la théorie et la pratique. En fait, cette erreur sur nos résultats est systématique.

Elle est due majoritairement à un problème de discrétisation. En effet, pour pouvoir calculer rapidement des intervalles assez conséquents, nous nous sommes limités à un pas d'espace de 0,1.

Ce pas sert notamment à intégrer C(x+y)Ф(y) dans I=[-2,2], soit 40 points d'intégration.

Comme la fonction Ф est approximée par des portes, ses variations sont brutales.
En x=a, nous avons du faire le choix entre Ф(a) = α ou β.
Nous avons choisi β.

Notre intégration est donc faussée sur une itération de deux points sur quarante.
C'est la principale source de différence entre les valeurs théorique et expérimentale.

En tenant compte de cette discrétisation, on trouve une valeur de kc théorique de 1,72 ce qui conduit à une erreur de 3% par rapport à la valeur expérimentale.

L'évolution de C en fonction de temps successifs est fournie en annexe.

Tests de validité du programme

Au vu de notre expérience toute relative de la programmation en C et de l'importance de la dite programmation dans notre cheminement, nous avons entrepris de tester le programme.

Nous avons d'abord testé indépendamment les subroutines simples à vérifier, via des tracés de courbes ou des calculs de valeurs rapidement prévisibles. Puis nous avons du testé l'agencement des subroutines à l'intérieur du programme.

Pour ce faire, nous avons utilisé 3 tests simples. Il s'agissait de modifier des données de départ du problème afin de le ramener à un problème connu et prévisible pouvant utiliser un algorithme similaire.

.dt=0. En remplaçant le pas de temps par 0, on peut parfaitement prévoir l'évolution du programme dans le temps, il ne doit pas évoluer du tout.
On a donc effectuer ce test avec quelques états initiaux que nous souhaitions retrouver intact comme des sinusoïdales ou du bruit. Ce test permet d'éviter plusieurs sources potentielles d'erreur. A la fois dans l'utilisation du temps, mais aussi dans les diverses initialisations et réinitialisations de variables.

.L'équation de la chaleur est tout à fait prévisible. Et il est possible de l'introduire dans notre programme. Tout d'abord, numériquement 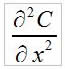s'écrit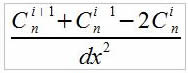

Soit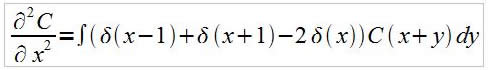

Ainsi, en modifiant les subroutines phi et dtc, on retombe sur un problème connu et prévisible qui nous permet de vérifier les subroutines autres que phi et dtc. Même si on ne localise pas précisément une erreur, on détecte sa présence.

.On a aussi essayé d'utiliser une fonction phi positive normée sur le domaine d'intégration.

En supposant C � peu pr�s constant et le régime stationnaire on obtient :


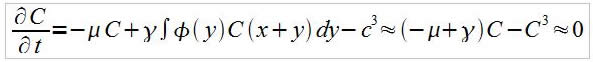
soit,

Sur le même principe que le test précédent, cette méthode a l'avantage de ne pas modifier dtc, et le désavantage de nécessiter une condition initiale quasi constante.

Et nous avons réitéré ces quelques tests lors des diverses modifications des programmes en s'assurant que les résultats restaient corrects.

Bien sur, nous n'excluons pas la présence d'erreurs dans notre travail, mais nous espérons avoir fortement fait diminuer la probabilité d'y trouver une erreur majeure.


page précédente page suivante